Polygon. Vertices, corners, sides and diagonals
polygon. Perimeter of a polygon.
Simple polygon. Convex polygon.
Sum of interior angles of a convex polygon.
A flat figure formed by a closed chain of segments is called polygon. Depending on the number of angles, a polygon can be a triangle, quadrilateral, pentagon, hexagon etc. Figure 17 shows the hexagon ABCDEF. Points A, B, C, D, E, F – vertices
Polygon; angles A, B, C, D, E, F – polygon angles; segments AC, AD, BE, etc. - diagonals; AB, BC, CD, DE, EF, FA – sides of a polygon; the sum of the lengths of the sides AB + BC + ... + FA is called the perimeter and is denoted p (sometimes denoted - 2p, then p is the semi-perimeter). In elementary geometry, only simple polygons are considered, the contours of which do not have self-intersections, as shown in Fig. 18. If all the diagonals lie inside the polygon, it is called convex. The hexagon in Fig. 17 is convex; the pentagon ABCDE in Fig. 19 is not convex, since its diagonal AD lies outside. The sum of the interior angles of a convex polygon is 180º (n – 2), where n is the number of angles (or sides) of the polygon.
Parallelogram. Properties and characteristics of a parallelogram.
Rectangle. Basic properties of a rectangle. Rhombus.
Square . Trapezoid. Midlines of trapezium and triangle.
A parallelogram (ABCD, Fig. 32) is a quadrilateral whose opposite sides are parallel in pairs. 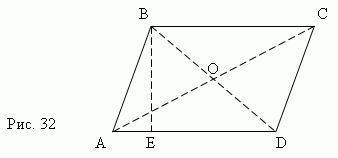
Any two opposite sides of a parallelogram are called its bases, and the distance between them is called its height (BE, Fig. 32).
Properties of a parallelogram.
1. Opposite sides of a parallelogram are equal(AB = CD, AD = BC).
2. Opposite angles of a parallelogram are equal(A=C, B=D).
3. The diagonals of a parallelogram are bisected at their intersection point.(AO = OC, BO = OD).
4. The sum of the squares of the diagonals of a parallelogram is equal to the sum of the squaresits four sides:
AC² + BD² = AB² + BC² + CD² + AD².
Signs of a parallelogram.
A quadrilateral is a parallelogram if one of the following conditions is true:
1. Opposite sides are equal in pairs(AB = CD, AD = BC).
2. Opposite angles are equal in pairs(A=C, B=D).
3. Two opposite sides are equal and parallel(AB = CD, AB || CD).
4.Diagonals bisect at their intersection point(AO = OC, BO = OD).
Rectangle.
Br />
If one of the angles of a parallelogram is right, then all other angles are also right (why?). Such a parallelogram is called a rectangle (Fig. 33).
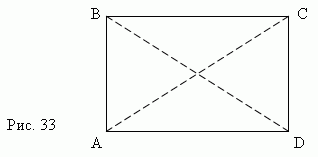
Basic properties of a rectangle.
The sides of a rectangle are also its heights.
The diagonals of the rectangle are equal: AC = BD.
The square of the diagonal of a rectangle is equal to the sum of the squares of its sides(see Pythagorean theorem above):
AC 2 = AD 2 + DC 2.
Rhombus. If all sides of a parallelogram are equal, then this parallelogram is called diamond (Fig. 34) .
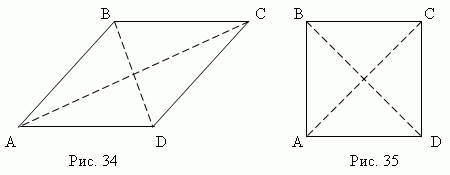
The diagonals of a rhombus are mutually perpendicular (AC BD) and bisect their angles (DCA = BCA, ABD = CBD, etc.).
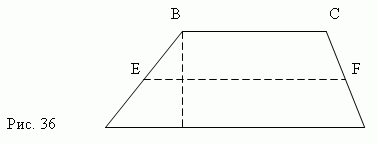
Square is parallelogram with right angles and equal sides (Fig. 35). A square is a special case of a rectangle and a rhombus at the same time; therefore, it has all of the above properties.
R />
Trapezoid is a quadrilateral whose opposite sides are one hundredthe rhones are parallel(Fig. 36).
Here AD || B.C. Parallel sides are called reasons trapezoid, and the other two (AB and CD) aresides.The distance between bases (BM) is height. Line segment EF connecting midpoints E and F
The lateral sides are called the midline of the trapezium. The midline of the trapezoid is equal to half the sum of the bases: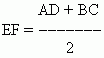
and parallel to them: EF || AD and EF || B.C.
A trapezoid with equal sides (AB = CD) is called an isosceles no trapezoid. In an equilateral trapezoid, the angles at each base are equal(A=D, B=C).
A parallelogram can be considered a special case of a trapezoid.
Middle line of the triangle- this is a segment connecting midpoints lateral sides of the triangle. The middle line of the triangle is equal to half th base and parallel to it. o property follows from the previous one
Point, since a triangle can be considered as a case of degeneration of a trapezoid, when one of its bases turns into a point.
A polygon inscribed in a circle.
A polygon circumscribed about a circle.
Described there is a circle around the polygon.
Inscribed into a polygon circle.
Radius of a circle inscribed in a triangle.
Radius of a circle circumscribed about a triangle .
Regular polygon.
Center and apothem of a regular polygon.
Ratios of sides and radii of regular polygons.
Inscribed in a circle called a polygon the vertices of which are located on the circle in Fig. 54). Described around a circle called a nogonwhose sides are tangent to the circle
(Fig. 55). 
Respectively, circle passing through the vertices of a polygon(Fig.54), calleddescribed about a polygon; circle, for in which the sides of the polygon are tangent (Fig. 55), on is called inscribed in a polygon. For arbitrary it is impossible to fit a polygon into it and draw a circle around it. For triangle Nick this is always possible.
Radius r of the inscribed circleexpressed through sides a, b, c triangle:
Radius R of the described circle expressed by the formula: 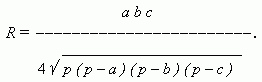
A circle can be inscribed in a quadrilateral if the sums of its opposite sides are equal.For parallelograms, this is only possible for a rhombus (square). The center of the inscribed circle is located at the point of intersection of the diagonals.A circle can be described around a quadrilateral if its sumopposite angles is equal 180º. For parallelograms, this is only possible for a rectangle (square). The center of the circumscribed circle lies at the point of intersection of the diagonals. You can describe a circle around a trapezoid if it is equilateral.r />
A regular polygon is a polygon with equal sides and angles.
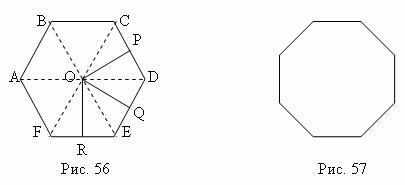
Fig. 56 shows a regular hexagon, and Fig. 57 shows a regular octagon. A regular quadrilateral is a square; a regular triangle is an equilateral triangle. Each angle of a regular polygon is equal to 180º (n – 2) / n, where n is the number of its angles. Inside a regular polygon there is a point O (Fig. 56), equidistant from all its vertices (OA = OB = OC = ... = OF), which is called the center of the regular polygon. The center of a regular polygon is also equidistant from all its sides (OP = OQ = OR = ...). The segments OP, OQ, OR, ... are called apothems; segments OA, OB, OC, ... are the radii of a regular polygon. A circle can be inscribed in a regular polygon and a circle can be described around it. The centers of the inscribed and circumscribed circles coincide with the center of a regular polygon. The radius of the circumcircle is the radius of a regular polygon, and the radius of the inscribed circle is its apothem. Ratios of sides and radii of regular polygons:
For most regular polygons, it is impossible to express the relationship between their sides and radii using an algebraic formula.
EXAMPLE Is it possible to cut a square with a side of 30 cm from a circle?
40 cm in diameter?
Solution: The largest square enclosed in a circle is an inscribed
Square. According to the above formula, its
Side is equal to:
Therefore, a square with a side of 30 cm cannot be cut
From a circle with a diameter of 40 cm.
The vertices of the polygon, and the segments are the sides of the polygon. Vertices of a polygon - page No. 1/1
Geometry 8th grade K.K.Kurginyan Part-1* (with an asterisk).
Polygon.
Definition: A polygon is a geometric figure that consists of a flat, closed broken line without self-intersections. The vertices of the broken line are called peaks polygon, and the segments are parties polygon.
The vertices of a polygon are called neighboring, if they are the ends of one of its sides. Line segments connecting non-adjacent vertices of a polygon are called diagonals .
External corner of a convex polygon at a given vertex is the angle adjacent to the interior angle of the polygon at this vertex. In general, an external angle is the difference between 180° and an internal angle; it can take values from -180° to 180°. The sum of the external angles of a polygon is 360°.
Convex polygon.
Polygonis called convex if:
DefinitionI -
for any two points inside it, the segment connecting them lies entirely in it.
DefinitionII - each internal angle is less than 180°.
DefinitionIII - all its diagonals lie completely inside it.
DefinitionIV –
it lies on one side of each straight line passing through its two neighboring vertices.
Sum of angles
n
-gon.
The sum of the angles of a convex n-gon is (n-2)∙180°.
The sum of the angles of a non-convex n-gon is also equal to (n-2)∙180°. (The proof is similar, but uses in addition the lemma that any polygon can be cut diagonally into triangles).
Number of diagonals
n
-gon.*
Theorem: The number of diagonals of any n-gon is n(n-3)2.
Proof: Let n be the number of vertices of the polygon, let us calculate p the number of possible different diagonals. Each vertex is connected by diagonals to all other vertices, except the two neighboring ones and, naturally, itself. Thus, n-3 diagonals can be drawn from one vertex; Let's multiply this by the number of vertices (n-3)∙n, however, we counted each diagonal twice (once for each end, therefore, we must divide by 2) - hence, p= n(n-3)2.
Problem*: Which convex polygon has 25 more diagonals than sides?
25+n = nn-32
50 + 2n = n 2 - 3n
n 2 - 5n - 50 = 0
Let's factorize
n 2 -25-5n -25 = 0
n=-5 does not satisfy,
because it doesn't exist
such a polygon
n = 10 satisfies
Answer: Decagon.
Shapes with equal diagonals.*
On surface there are two regular polygons with all diagonals are equal among themselves - this square And regular pentagon (pentagon). A square has two identical diagonals that intersect at a right angle in the center. A regular pentagon has five identical diagonals, which together form the pattern of a five-pointed star (pentagram).

In space there is only one correct one polyhedron (not a polygon), which one all diagonals are equal among themselves - this regular octahedron (octahedron). At the octahedron three diagonals that intersect in pairs perpendicularly in the center. All diagonals of the octahedron are spatial (the octahedron has no diagonals of faces, since it has triangular faces).
In addition to the octahedron, there is another regular polyhedron, which all spatial diagonals are equal among themselves - this cube (hexahedron), in addition to spatial ones, the cube has diagonals of faces. The cube has four identical spatial diagonals that intersect in the center. The angle between the diagonals of a cube is either arccos (1/3) ≈ 70.5° (for a pair of diagonals drawn to adjacent vertices) or arccos (–1/3) ≈ 109.5° (for a pair of diagonals drawn to non-adjacent vertices ).
Quadrilaterals.
Each quadrilateral has four vertices, four sides and two diagonals.
Two non-adjacent sides are called opposite sides.
Two non-adjacent vertices are called opposite.
1.Parallelogram
is a quadrilateral whose opposite sides are parallel in pairs.

Properties of a parallelogram:
1) Opposite sides of a parallelogram are equal. AB=DC, AD=BC.
2) Opposite angles of a parallelogram are equal. A=C, B=D.
3) The diagonals of a parallelogram intersect and are divided in half by the intersection point. AO=OC, BO=OD.
4) The sum of angles adjacent to one side is 180°. A+D=180, A+B=180, B+C=180, D+C=180.
5) The sum of all angles is 360°. A+B+C+D=360°.
6)* The sum of the squares of the diagonals of a parallelogram is equal to twice the sum of the squares of its two adjacent sides: AC 2 +BD 2 =2∙(AB 2 +AD 2).
Problem 1*: Find the diagonal of a parallelogram if it is known that the length of one diagonal is AC = 9 cm, and the sides AD = 7 cm and AB = 4 cm.
Solution: Substituting the values into the formula we get:
81+BD 2 =2∙(49+16),
BD 2 =49, therefore the second diagonal is BD = 7 cm. Answer: 7 cm.
Problem 2*: Find the diagonal of a parallelogram if it is known that the length of one diagonal is BD=10 cm, and the sides AD=8 cm and AB=2 cm.
Solution: The conditions of the problem are not true, since the sum of two sides of a triangle is always greater than the third side. Answer: the problem has no solutions (meaning).
Problem 3*: a) Find the side of the parallelogram if it is known that the length of the diagonals is BD = 6 cm, AC = 8, and one side AB = 5 cm. b) What is the name of this parallelogram.
Problem 4**: The sum of the lengths of the diagonals of a parallelogram is 12 cm, and the product of 32, find the value of the sum of the squares of all its sides.
Problem 5**: Find the largest perimeter of a parallelogram whose diagonals are 6 cm and 8 cm.
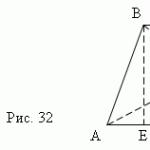
Solution: Let's prove that among all parallelograms with given diagonal lengths, the rhombus has the largest perimeter .
Indeed, let a And b are the lengths of adjacent sides of the parallelogram, and and are the lengths of its diagonals (see Fig. 2). Then the perimeter of the parallelogram is: P = 2(a + b).
From the equality expressing the theorem on the sum of the squares of the diagonals of a parallelogram, it follows that for all parallelograms with given diagonals, the sum of the squares of the sides is a constant value.
According to the inequality between the arithmetic mean and the mean square: , and equality is achieved t. and t. t., when a = b. This means that the parallelogram with the largest perimeter is a rhombus. Find the side of this rhombus: =5(cm). Answer: 20 cm.
2.Rectangle
is a parallelogram in which all angles are right.
Definition 2: This is a quadrilateral with all right angles.
Definition 3: It is a parallelogram with one right angle.
Definition 4: It is a parallelogram whose angles are equal.
Rectangle properties:
+
1) The diagonals of the rectangle are equal.
2)* The square of the diagonal is equal to the sum of the squares of the sides. AC 2 =AB 2 +DC 2
Task 1: The shortest side of the rectangle is 5cm, the diagonals intersect at an angle of 60°. Find the diagonals of the rectangle.
Task 2: The shortest side of a rectangle is 24, the diagonals intersect at an angle of 120°. Find the diagonals and the longest side of the rectangle.
Problem 3*: The side of the rectangle is 3 cm, the diagonal is 5 cm. Find the other side of the rectangle.
Problem 4*: The side of the rectangle is 6 cm, the diagonal is 10 cm. Find the area of the rectangle.
3.Rhombus
is a parallelogram in which all sides are equal.
Definition 2: It is a quadrilateral with all sides equal.
Properties of a rhombus:
same properties as a parallelogram +
1) The diagonals of a rhombus are mutually perpendicular (AC ⊥ BD).
2) The diagonals of a rhombus divide its angles in half (that is, the diagonals of a rhombus are the bisectors of its angles - ∠DCA = ∠BCA, ∠ABD = ∠CBD, ∠BAC = ∠DAC, ∠ADB = ∠CDB).
3)*The sum of the squares of the diagonals is equal to the square of the side multiplied by 4 (a consequence of the parallelogram identity). AC 2 +BD 2 =4 AB 2
Task 1: The diagonals of the rhombus are 6 and 8 cm. Find the side of the rhombus.
Task 2: The side of the rhombus is 10 cm, one of the angles is 60. Find the small diagonal of the rhombus.
4.Square
is a parallelogram in which all angles are equal to 90 and all sides are equal.
Definition 2: This is a parallelogram in which all angles and sides are equal to each other.
Definition 3: This is a quadrilateral in which all angles and sides are equal to each other.
Definition 4: This is a rhombus with one right angle.
Definition 5: This is a rhombus whose angles are equal.
Definition 6: It is a rectangle with all sides equal.
Properties of a square:
same properties as a parallelogram +
1) The diagonals of a square are equal.
2) The diagonals of the square are mutually perpendicular (AC ⊥ BD).
3) The diagonals of a square divide its angles in half (that is, the diagonals of a square are the bisectors of its angles - ∠DCA = ∠BCA= ∠ABD = ∠CBD= ∠BAC = ∠DAC= ∠ADB = ∠CDB=45).
4)* The square of the diagonal is equal to twice the square of the side. AC 2 =2 AB 2
5.Trapezoid is a quadrilateral in which two sides are parallel and the other two are not parallel.
The parallel sides are called bases, and the other two are called lateral sides.
A trapezoid is called isosceles if its sides are equal.
A trapezoid is called rectangular if one of its angles is right.
Task: Prove that a trapezoid cannot be both rectangular and isosceles.
Definition
Top corner
The vertex of the angle is the point where the two rays originate.
The vertex of the angle is the point where the two rays originate; where two segments meet; where two lines intersect; where is any combination of rays, segments and lines that form two (straight-line) “sides” that converge at one point.
Vertex of polygon polyhedron
In a polygon, a vertex is called "convex" if the interior angle of the polygon is less than π radians (180° is two right angles). Otherwise the vertex is called "concave".
More generally, a vertex of a polyhedron is convex if the intersection of the polyhedron with a sufficiently small sphere having the vertex as its center is a convex figure; otherwise the apex is concave.
The vertices of a polyhedron are related to the vertices of a graph, since a polyhedron is a graph whose vertices correspond to the vertices of a polyhedron, and therefore the graph of a polyhedron can be considered as a one-dimensional simplicial complex whose vertices are the vertices of the graph. However, in graph theory, vertices can have fewer than two incident edges, which is usually not allowed for geometric vertices. There is also a connection between geometric vertices and the vertices of the curve, the points of extrema of its curvature - the vertices of the polygon are in a sense points of infinite curvature, and if the polygon is approximated by a smooth curve, the points of extreme curvature will lie near the vertices of the polygon. However, approximating the polygon using a smooth curve gives additional vertices at the points of minimum curvature.
Vertices of flat mosaics
"Ears"
"Mouths"
Main peak x i (\displaystyle x_(i)) simple polygon P (\displaystyle P) called "mouth" if the diagonal [ x i − 1 , x i + 1 ] (\displaystyle ) lies outside P (\displaystyle P).
Number of vertices of a polyhedron
Any surface of a three-dimensional convex polyhedron has the Euler characteristic:
V − E + F = 2 , (\displaystyle V-E+F=2,)Where V (\displaystyle V)- number of vertices, E (\displaystyle E)- number of edges, and F (\displaystyle F)- number of faces. This equality is known as Euler's equation. For example, a cube has 12 edges and 6 faces, and therefore 8 vertices: 8 − 12 + 6 = 2 (\displaystyle 8-12+6=2) .
Peaks in computer graphics
In computer graphics, objects are often represented as triangulated polyhedra, in which the vertices of an object are associated not only with three spatial coordinates, but also with other graphic information necessary for the correct construction of an image of an object, such as color, reflectivity, texture, and vertex normals. These properties are used when constructing an image using
In the section on the question Explain what shape is called a polygon. What are the vertices, sides, diagonals and perimeter of a polygon? given by the author Arek Grigoryan the best answer is A polygon is a geometric figure, defined as a closed broken line.
The vertices of the polygon are called the vertices of the polygon, and the segments are called the sides of the polygon.
The segments connecting non-adjacent vertices of a polygon are called diagonals.
The perimeter of a polygon is the sum of the lengths of all the polygons.
Source: Thanks to Yandex for this
Answer from Baby[guru]
Answer from Neurologist[newbie]
The answer is CUT!!!
Answer from Individual[newbie]
thanks a lot
Answer from Sheet[newbie]
polygon - a figure with more than 4 angles.
vertex - the vertex of an angle, the point of intersection of two sides.
side - well, actually - side))) such a stick from which it is composed
diagonal - a line drawn from one corner to another
perimeter - the sum of the lengths of all sides
Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.
Collection and use of personal information
Personal information refers to data that can be used to identify or contact a specific person.
You may be asked to provide your personal information at any time when you contact us.
Below are some examples of the types of personal information we may collect and how we may use such information.
What personal information do we collect:
- When you submit an application on the site, we may collect various information, including your name, telephone number, email address, etc.
How we use your personal information:
- The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
- From time to time, we may use your personal information to send important notices and communications.
- We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
- If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.
Disclosure of information to third parties
We do not disclose the information received from you to third parties.
Exceptions:
- If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government authorities in the territory of the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
- In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.
Protection of personal information
We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.
Respecting your privacy at the company level
To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.