Seguimos ocupándonos de sistemas de ecuaciones lineales. Hasta ahora, hemos analizado sistemas que tienen una única solución. Dichos sistemas se pueden resolver de cualquier manera: método de sustitución("Colegio"), por fórmulas de Cramer, método matricial, Método gaussiano... Sin embargo, en la práctica, hay dos casos más generalizados cuando:
1) el sistema es incompatible (no tiene soluciones);
2) el sistema tiene infinitas soluciones.
Para estos sistemas, se utiliza el método de solución más universal: Método de Gauss... De hecho, el método de la "escuela" conducirá a la respuesta, pero en matemáticas superiores se acostumbra utilizar el método gaussiano de eliminación sucesiva de incógnitas. Aquellos que no estén familiarizados con el algoritmo del método gaussiano, primero estudien la lección. Método de Gauss
Las transformaciones de la matriz elemental en sí son exactamente las mismas, la diferencia estará al final de la solución. Primero consideremos un par de ejemplos cuando el sistema no tiene soluciones (inconsistente).
Ejemplo 1
¿Qué le llama la atención de inmediato en este sistema? El número de ecuaciones es menor que el número de variables. Hay un teorema que establece: "Si el número de ecuaciones del sistema es menor que el número de variables, entonces el sistema es inconsistente o tiene infinitas soluciones ". Y solo queda descubrirlo.
El comienzo de la solución es completamente ordinario: escribimos la matriz extendida del sistema y, usando transformaciones elementales, la llevamos a una forma escalonada:
(1). En el paso superior izquierdo, necesitamos obtener (+1) o (–1). No hay tales números en la primera columna, por lo que reorganizar las filas no hará nada. La unidad tendrá que organizarse de forma independiente, y esto se puede hacer de varias formas. Hicimos esto. A la primera línea agregue la tercera línea multiplicada por (–1).
(2). Ahora tenemos dos ceros en la primera columna. A la segunda línea agregamos la primera línea multiplicada por 3. A la tercera línea agregamos la primera línea multiplicada por 5.
(3). Después de la transformación realizada, siempre es recomendable mirar y ¿es posible simplificar las líneas resultantes? Poder. Divida la segunda fila por 2, al mismo tiempo obteniendo el deseado (–1) en el segundo paso. Divida la tercera fila por (–3).
(4). Agregue la segunda línea a la tercera línea. Probablemente todos prestaron atención a la mala línea que resultó como resultado de transformaciones elementales:
... Está claro que esto no puede ser así.
De hecho, reescribimos la matriz resultante
volviendo al sistema de ecuaciones lineales:
Si, como resultado de transformaciones elementales, una cadena de la forma , dóndeλ - un número distinto de cero, entonces el sistema es incompatible (no tiene soluciones).
¿Cómo registro el final de una tarea? Debes escribir la frase:
“Como resultado de transformaciones elementales, se obtuvo una cadena de la forma, donde λ ≠ 0 ". Respuesta: "El sistema no tiene soluciones (inconsistente)".
Tenga en cuenta que en este caso no hay retroceso del algoritmo gaussiano, no hay soluciones y simplemente no hay nada que encontrar.
Ejemplo 2
Resolver un sistema de ecuaciones lineales 
Este es un ejemplo de una solución "hágalo usted mismo". Solución completa y respuesta al final del tutorial.
Nuevamente, le recordamos que su curso de solución puede diferir de nuestro curso de solución, el método de Gauss no especifica un algoritmo inequívoco, debe adivinar sobre el orden de las acciones y las acciones en sí mismas en cada caso de forma independiente.
Otra característica técnica de la solución: las transformaciones elementales se pueden detener inmediatamente, tan pronto como apareció una línea del formulario, donde λ ≠ 0 ... Considere un ejemplo condicional: suponga que después de la primera transformación se obtiene la matriz
.
Esta matriz aún no se ha reducido a una forma escalonada, pero no hay necesidad de más transformaciones elementales, ya que ha aparecido una fila de la forma, donde λ ≠ 0 ... Debe responder inmediatamente que el sistema es incompatible.
Cuando un sistema de ecuaciones lineales no tiene soluciones, esto es casi un regalo para el estudiante, ya que se obtiene una solución corta, a veces literalmente en 2-3 pasos. Pero todo en este mundo está equilibrado, y el problema en el que el sistema tiene infinitas soluciones es simplemente más largo.
Ejemplo 3:
Resolver un sistema de ecuaciones lineales
Hay 4 ecuaciones y 4 incógnitas, por lo que el sistema puede tener una sola solución, no tener soluciones o tener infinitas soluciones. Sea como sea, pero el método de Gauss nos llevará a la respuesta de todos modos. Ésta es su versatilidad.
El comienzo vuelve a ser estándar. Escribamos la matriz extendida del sistema y, usando transformaciones elementales, traigamos a una forma escalonada:
Eso es todo y tenías miedo.
(1). Tenga en cuenta que todos los números de la primera columna son divisibles por 2, por lo que estamos satisfechos con los dos del paso superior izquierdo. A la segunda línea agregue la primera línea multiplicada por (–4). A la tercera línea, agregue la primera línea multiplicada por (–2). A la cuarta línea, agregue la primera línea multiplicada por (–1).
¡Atención! Muchos pueden ser tentados desde la cuarta línea. sustraer primera linea. Esto se puede hacer, pero no es necesario, la experiencia muestra que la probabilidad de un error en los cálculos aumenta varias veces. Simplemente agregue: a la cuarta línea agregue la primera línea multiplicada por (–1) - ¡exactamente!
(2). Las últimas tres líneas son proporcionales, dos de ellas se pueden eliminar. Aquí de nuevo necesitas mostrar mayor atención, pero ¿son las líneas realmente proporcionales? Para estar seguro, no será superfluo multiplicar la segunda línea por (–1) y dividir la cuarta línea por 2, lo que da como resultado tres líneas idénticas. Y solo entonces borre dos de ellos. Como resultado de las transformaciones elementales, la matriz expandida del sistema se reduce a una forma escalonada:
Al completar una tarea en un cuaderno, es recomendable hacer las mismas notas a lápiz para mayor claridad.
Reescribamos el sistema de ecuaciones correspondiente: 
La única solución del sistema aquí no huele como "habitual". Una mala linea donde λ ≠ 0, también no. Esto significa que este es el tercer caso restante: el sistema tiene infinitas soluciones.
Se escribe brevemente un número infinito de soluciones del sistema en la forma del llamado solución general del sistema.
Encontraremos la solución general del sistema utilizando el curso inverso del método de Gauss. Para sistemas de ecuaciones con un conjunto infinito de soluciones, aparecen nuevos conceptos: "Variables básicas" y "Variables libres"... Primero, definamos qué variables tenemos básico y qué variables - gratis... No es necesario explicar en detalle los términos del álgebra lineal, basta recordar que existen tales variables basicas y variables libres.
Las variables básicas siempre "se sientan" estrictamente en los pasos de la matriz.... En este ejemplo, las variables básicas son X 1 y X 3 .
Las variables libres lo son todo restante variables que no obtuvieron un escalón. En nuestro caso, hay dos de ellos: X 2 y X 4 - variables libres.
Ahora necesitas todosvariables basicas para expresar solo a travésvariables libres... El reverso del algoritmo gaussiano funciona tradicionalmente de abajo hacia arriba. A partir de la segunda ecuación del sistema, expresamos la variable básica X 3:
Ahora veamos la primera ecuación: 
... Primero, sustituimos la expresión encontrada en ella:
Queda por expresar la variable básica X 1 a través de variables libres X 2 y X 4:
Al final, tenemos lo que necesitamos. todos variables básicas ( X 1 y X 3) expresado solo a través variables libres X 2 y X 4):
De hecho, la solución general está lista:
.
¿Cómo escribir correctamente la solución general? En primer lugar, las variables libres se escriben en la solución general "por sí mismas" y estrictamente en su lugar. En este caso, variables libres X 2 y X 4 debe escribirse en la segunda y cuarta posiciones:
.
Las expresiones obtenidas para las variables básicas y, obviamente, debes escribir en la primera y tercera posición:
De la solución general del sistema, puede encontrar infinitos soluciones privadas... Es muy simple. Variables libres X 2 y X 4 se llaman así porque se les puede dar cualquier valor final... Los valores más populares son cero, porque esta es la forma más fácil de obtener la solución en particular.
Sustituyendo ( X 2 = 0; X 4 = 0) en la solución general, obtenemos una de las soluciones particulares:
, o es una solución particular correspondiente a variables libres en valores ( X 2 = 0; X 4 = 0).
Las unidades son otra dulce pareja, sustituto ( X 2 = 1 y X 4 = 1) en una solución general:
, es decir, (-1; 1; 1; 1) es otra solución particular.
Es fácil ver que el sistema de ecuaciones tiene infinitas soluciones, ya que podemos dar variables libres alguna valores.
Cada la solución particular debe satisfacer a cada ecuación del sistema. Ésta es la base para la verificación "rápida" de la corrección de la solución. Tome, por ejemplo, una solución particular (-1; 1; 1; 1) y sustitúyala en el lado izquierdo de cada ecuación del sistema original:
Todo debería encajar. Y con cualquier decisión en particular que reciba, todo también debe estar de acuerdo.
Estrictamente hablando, comprobar una solución en particular a veces engaña, es decir, alguna solución particular puede satisfacer cada ecuación del sistema, pero la solución general en sí misma se encuentra incorrectamente. Por lo tanto, en primer lugar, la verificación de la solución general es más completa y confiable.
Cómo comprobar la solución general resultante 
?
No es difícil, pero requiere muchas transformaciones que requieren mucho tiempo. Necesitas tomar expresiones básico variables, en este caso 
y, y sustitúyalos en el lado izquierdo de cada ecuación del sistema.
En el lado izquierdo de la primera ecuación del sistema:
Se obtiene el lado derecho de la primera ecuación inicial del sistema.
En el lado izquierdo de la segunda ecuación del sistema:
Se obtiene el lado derecho de la segunda ecuación original del sistema.
Y más allá, a los lados izquierdos de la tercera y cuarta ecuaciones del sistema. Esta comprobación lleva más tiempo, pero garantiza la exactitud del cien por cien de la solución global. Además, en algunas tareas, es precisamente la verificación de la solución general lo que se requiere.
Ejemplo 4:
Resuelva el sistema por el método gaussiano. Encuentre una solución general y dos particulares. Verifique la solución general.
Este es un ejemplo de una solución "hágalo usted mismo". Aquí, por cierto, nuevamente el número de ecuaciones es menor que el número de incógnitas, lo que significa que queda inmediatamente claro que el sistema será incompatible o con un conjunto infinito de soluciones.
Ejemplo 5:
Resuelve un sistema de ecuaciones lineales. Si el sistema tiene infinitas soluciones, encuentre dos soluciones particulares y verifique la solución general
Solución: Escribamos la matriz extendida del sistema y, usando transformaciones elementales, traigamos a una forma escalonada:
(1). Agregue la primera línea a la segunda línea. A la tercera línea agregamos la primera línea multiplicada por 2. A la cuarta línea agregamos la primera línea multiplicada por 3.
(2). A la tercera línea, agregue la segunda línea multiplicada por (–5). A la cuarta línea, agregue la segunda línea multiplicada por (–7).
(3). La tercera y cuarta líneas son iguales, borramos una de ellas. Aquí hay tanta belleza:
Las variables básicas se sientan en peldaños, por lo tanto, variables básicas.
Solo hay una variable libre que no obtuvo un paso aquí :.
(4). Movimiento inverso. Expresemos las variables básicas en términos de una variable libre:
De la tercera ecuación:
Considere la segunda ecuación y sustituya la expresión encontrada en ella:
, 
, ,
Considere la primera ecuación y sustituya las expresiones encontradas y en ella:
Por tanto, la solución general para una variable libre es X 4:
Una vez más, ¿cómo surgió? Variable libre X 4 se sienta solo en el cuarto lugar que le corresponde. Las expresiones resultantes para las variables básicas también están en su lugar.
Revisemos la solución general de inmediato.
Sustituimos las variables básicas ,, en el lado izquierdo de cada ecuación del sistema:
Se obtienen los correspondientes lados derechos de las ecuaciones, por lo que se encuentra la solución general correcta.
Ahora de la solución común encontrada 
obtenemos dos soluciones particulares. Todas las variables se expresan aquí mediante un único variable libre x 4. No necesitas romperte la cabeza.
Permitir X 4 = 0, entonces 
- la primera solución particular.
Permitir X 4 = 1, entonces 
- una solución más particular.
Respuesta: Decisión común: ... Soluciones privadas:
y .
Ejemplo 6:
Encuentre la solución general de un sistema de ecuaciones lineales.
Ya hemos comprobado la decisión general, se puede confiar en la respuesta. Su curso de decisión puede diferir de nuestro curso de decisión. Lo principal es que las decisiones comunes coincidan. Probablemente, mucha gente notó un momento desagradable en las soluciones: muy a menudo, durante el curso inverso del método de Gauss, tuvimos que jugar con fracciones ordinarias... En la práctica, esto es cierto, los casos en los que no hay fracciones son mucho menos comunes. Esté preparado mentalmente y, lo más importante, técnicamente.
Detengámonos en las características de la solución que no se encontraron en los ejemplos resueltos. La solución general del sistema a veces puede incluir una constante (o constantes).
Por ejemplo, la solución general es :. Aquí una de las variables básicas es igual a un número constante :. No hay nada exótico en esto, sucede. Obviamente, en este caso, cualquier solución particular contendrá una A en la primera posición.
Rara vez, pero hay sistemas en los que el número de ecuaciones es mayor que el número de variables... Sin embargo, el método de Gauss funciona en las condiciones más duras. Es necesario reducir con calma la matriz expandida del sistema a una forma escalonada de acuerdo con el algoritmo estándar. Un sistema así puede ser inconsistente, puede tener infinitas soluciones y, curiosamente, puede tener una única solución.
Repitamos nuestro consejo: para sentirse cómodo al resolver un sistema usando el método gaussiano, debe llenar su mano y resolver al menos una docena de sistemas.
Soluciones y Respuestas:
Ejemplo 2:
Solución:Anotemos la matriz extendida del sistema y, usando transformaciones elementales, traigamos a una forma escalonada.
Transformaciones elementales realizadas:
(1) La primera y la tercera línea están invertidas.
(2) La primera línea multiplicada por (–6) se agregó a la segunda línea. La primera línea multiplicada por (–7) se agregó a la tercera línea.
(3) La segunda línea multiplicada por (–1) se agregó a la tercera línea.
Como resultado de transformaciones elementales, una cadena de la forma, dónde λ ≠ 0 .Esto significa que el sistema es incompatible.Respuesta: sin soluciones.
Ejemplo 4:
Solución:Escribamos la matriz extendida del sistema y, usando transformaciones elementales, traigamos a una forma escalonada:
Conversiones realizadas:
(1). La primera línea multiplicada por 2 se agregó a la segunda línea. La primera línea multiplicada por 3 se agregó a la tercera línea.
No hay nadie para el segundo paso , y la transformación (2) tiene como objetivo su obtención.
(2). La tercera línea se agregó a la segunda línea multiplicada por –3.
(3). La segunda y tercera líneas se intercambiaron (reorganizó el -1 resultante al segundo paso)
(4). La tercera línea se agregó a la segunda línea multiplicada por 3.
(5). Se cambió el signo de las dos primeras líneas (multiplicado por -1), la tercera línea se dividió por 14.
Marcha atrás:
(1). Aquí - variables básicas (que están en los pasos), y - variables libres (que no consiguieron un paso).
(2). Expresemos las variables básicas en términos de variables libres:
De la tercera ecuación: .
(3). Considere la segunda ecuación:, soluciones particulares:
Respuesta: Decisión común: 
Números complejos
En esta sección, nos familiarizaremos con el concepto. Número complejo, considerar algebraico, trigonométrico y forma ejemplar Número complejo. También aprenderemos a realizar acciones con números complejos: suma, resta, multiplicación, división, exponenciación y extracción de raíces.
Para dominar los números complejos, no necesita ningún conocimiento especial del curso de matemáticas superiores, y el material está disponible incluso para un estudiante. Basta con poder realizar operaciones algebraicas con números "ordinarios" y recordar la trigonometría.
Recordemos primero los números "ordinarios". En matemáticas, se les llama conjunto de números reales y denotado por la letra R, o R (espesado). Todos los números reales se encuentran en la conocida recta numérica:
La compañía de los números reales es muy variada: aquí hay números enteros, fracciones y números irracionales. En este caso, cada punto del eje numérico corresponde necesariamente a algún número real.
Encontrar soluciones a un sistema linealAplicaciones portátiles de Windows en Bodrenko.com
§2. Encontrar soluciones a un sistema lineal
El teorema de Kronecker-Capelli establece una condición necesaria y suficiente para la compatibilidad de un sistema lineal, pero no proporciona una forma de encontrar soluciones a este sistema.
En esta sección, buscaremos soluciones para el sistema lineal (3.1). Primero, consideramos el caso más simple de un sistema cuadrático de ecuaciones lineales con un determinante distinto de cero de la matriz básica, y luego procedemos a encontrar el conjunto de todas las soluciones de un sistema lineal general de la forma (3.1).
1. Un sistema cuadrático de ecuaciones lineales con un determinante distinto de cero de la matriz básica. Sea dado un sistema cuadrático de ecuaciones lineales
con un determinante Δ distinto de cero de la matriz principal
Demostremos que tal sistema tiene, y además, una solución única, y encontraremos esta solución. Primero, probamos que el sistema (3.10) solo puede tener una solución (es decir, probamos la unicidad de una solución al sistema (3.10) bajo el supuesto de su existencia).
Suponga que existen algunos n números x 1, x 2, ..., xn tales que cuando estos números se sustituyen en el sistema (3.10), todas las ecuaciones de este sistema se convierten en identidades (es decir, hay una solución para el sistema (3.10) x 1, x 2, ..., x n). Luego, multiplicando las identidades (3.10), respectivamente, por los complementos algebraicos A 1j, A 2j, ..., A nj de los elementos j-ro de la columna del determinante Δ de la matriz (3.11) y luego sumando las identidades resultantes, obtenemos obtener (para cualquier número j, igual a 1, 2, ..., n)
Teniendo en cuenta que la suma de los productos de los elementos de la i-ésima columna por los correspondientes complementos algebraicos de los elementos de la columna j-ro es igual a cero para i ≠ j y es igual al determinante Δ de la matriz (3.11 ) para i = j (ver propiedad 4 ° de la subsección 4 del § 2, cap. 1), obtenemos de la última igualdad
x j Δ = segundo 1 UNA 1j + segundo 2 UNA 2j + ... + segundo norte UNA nj. (3,12)
Denotemos por el símboloΔ
j (B I ) (o, más brevemente, el símboloΔ
j ) determinante obtenido del determinanteΔ
de la matriz principal (3.11) reemplazando su j-ésima columna con una columna de términos libres b 1
, B 2
, ..., B norte (manteniendo todas las demás columnas sin cambios
Δ
).
Nótese que en el lado derecho de (3.12) está precisamente el determinante Δ j (bi) (para estar convencido de esto, basta escribir la expansión del determinante Δ j (bi) en términos de los elementos de la enésima columna), y esta igualdad toma la forma
Δ x j = Δ j (3.13)
Dado que el determinante Δ de la matriz (3.11) es distinto de cero, las igualdades (3.13) son equivalentes a las relaciones
Entonces, hemos probado que si la solución x 1
, X 2
, ..., NS norte sistema (3.10) con determinanteΔ
de la matriz principal (3.11) distinta de cero existe, entonces esta solución está determinada de forma única por las fórmulas (3.14).
Las fórmulas (3.14) se llaman Fórmulas de Cramer.
Recalcamos una vez más que hasta ahora hemos obtenido las fórmulas de Cramer bajo el supuesto de la existencia de una solución y demostramos su unicidad.
Queda por probar la existencia de una solución al sistema (3.10). Para ello, en virtud del teorema de Kronecker-Capelli, basta con demostrar que el rango de la matriz principal (3.11) es igual al rango de la matriz extendida (también hay otra forma de probar la existencia de una solución al sistema (3.10), que consiste en comprobar que los números x 1, x 2 ,. .., х n, definidos por las fórmulas de Cramer (3.14), convierten todas las ecuaciones del sistema (3.10) en identidades)
pero esto es obvio, porque en virtud de la relación Δ ≠ 0, el rango de la matriz principal es igual an, y el rango de la matriz extendida (3.15) que contiene n filas no puede ser mayor que n y por lo tanto es igual al rango de la matriz principal.
Esto prueba completamente que el sistema cuadrático de ecuaciones lineales (3.10) con un determinante distinto de cero de la matriz básica tiene, y además, una solución única determinada por las fórmulas de Cramer (3.14).
La afirmación que hemos probado se puede establecer aún más fácilmente en forma de matriz. Para hacer esto, reemplazamos (como en la subsección 1 del § 1) el sistema (3.10) con la ecuación matricial equivalente
AX = B, (3,16)
donde A es la matriz principal del sistema (3.11), y X y B son columnas,
el primero de los cuales se determinará y el segundo se dará.
Dado que el determinante Δ de la matriz A es distinto de cero, entonces existe una matriz inversa A -1 (ver párrafo 7 del §2, Capítulo 1).
Suponga que hay una solución para el sistema (3.10), es decir hay una columna X que hace que la ecuación matricial (3.16) sea una identidad. Multiplicando la identidad indicada a la izquierda por la matriz inversa А -1 tendremos
A -1 (AX) = A -1 B. (3.17)
Tengamos ahora en cuenta que en virtud de la propiedad combinatoria del producto de tres matrices (ver subsección 2 del § 1 del Capítulo 1) y en virtud de la relación A -1 A = E, donde E es la matriz unitaria (ver § 7 del § 2 del Capítulo 1), A -1 (AX) = (A -1 A) X = EX = X, entonces obtenemos de (3.17)
X = A -1 B. (3,18)
Ampliando la igualdad (3.18) y teniendo en cuenta la forma de la matriz inversa (ver fórmula A.41) de la Sección 7, Sección 2, Cap. 1), obtenemos las fórmulas de Cramer para los elementos de la columna X.
Entonces, hemos probado que si existe una solución para la ecuación matricial (3.16), entonces está determinada de manera única por la relación (3.18), que es equivalente a las fórmulas de Cramer.
Es fácil comprobar que la columna X definida por la relación (3.18) es de hecho una solución a la ecuación matricial (3.16),
es decir, cuando se sustituye en esta ecuación, la convierte en una identidad. De hecho, si la columna X se define por igualdad (3.18), entonces AX = A (A -1 B) = (AA -1) B = EB = B.
Entonces, si el determinante Δ de la matriz A es distinto de cero (es decir, si esta matriz no es degenerada), entonces existe, y además, una solución única para la ecuación matricial (3.16), definida por la relación (3.18), equivalente a las fórmulas de Cramer.
Ejemplo. Encontremos la solución al sistema cuadrático de ecuaciones lineales
con un determinante distinto de cero de la matriz principal
En la medida en
entonces, en virtud de las fórmulas de Cramer, la única solución del sistema en consideración tiene la forma x 1 = 1, x 2 = 2, x 3 = 3, x 4 = 4.
El significado principal de las fórmulas de Cramer es que dan una expresión explícita para resolver un sistema cuadrático de ecuaciones lineales (con un determinante distinto de cero) en términos de los coeficientes de las ecuaciones y términos libres. El uso práctico de las fórmulas de Cramer está asociado con cálculos bastante engorrosos (para resolver un sistema de n ecuaciones con n incógnitas, es necesario calcular el determinante (n + 1) del n-ésimo orden). Debe agregarse a esto que si los coeficientes de las ecuaciones y los términos libres son solo valores aproximados de cualquier cantidad física medida o se redondean en el proceso de cálculos, entonces el uso de las fórmulas de Cramer puede conducir a grandes errores y en algunos casos es inapropiado.
En la Sección 4, Capítulo 4, el método de regularización debido a A.N. Tikhonov y le permite encontrar una solución a un sistema lineal con una precisión correspondiente a la precisión de especificar la matriz de coeficientes de ecuaciones y una columna de términos libres, y en el Cap. 6 da una idea de los llamados métodos iterativos para la resolución de sistemas lineales, que permiten resolver estos sistemas mediante aproximaciones sucesivas de incógnitas.
En conclusión, observamos que en esta subsección hemos excluido de consideración el caso de desaparición del determinante Δ de la matriz principal del sistema (3.10). Este caso estará contenido en la teoría general de sistemas de m ecuaciones lineales con n incógnitas, que se presenta en la siguiente subsección.
2. Encontrar todas las soluciones de un sistema lineal general. Considere ahora un sistema general de m ecuaciones lineales con n incógnitas (3.1). Suponga que este sistema es consistente y que el rango de sus matrices principal y extendida es igual a r. Sin pérdida de generalidad, podemos suponer que el menor básico de la matriz principal (3.2) está en la esquina superior izquierda de esta matriz (el caso general se reduce a este caso permutando ecuaciones e incógnitas en el sistema (3.1)).
Entonces, las primeras r filas tanto de la matriz principal (3.2) como de la matriz extendida (3.8) son las filas base de estas matrices (dado que los rangos de las matrices principal y extendida son ambos iguales a r, la base menor de la matriz principal será simultáneamente la base menor de la matriz extendida), y, por el Teorema 1.6 sobre el menor básico, cada una de las filas de la matriz extendida (1.8), comenzando por la (r + 1) ésima fila, es una combinación lineal de las primeras r filas de esta matriz.
En términos del sistema (3.1), esto significa que cada una de las ecuaciones de este sistema, comenzando con la (r + 1) ésima ecuación, es una combinación lineal (es decir, una consecuencia) de las primeras r ecuaciones de este sistema ( es decir, cualquier solución de las primeras r ecuaciones del sistema (3.1) se convierte en identidades y todas las ecuaciones subsiguientes de este sistema).
Por lo tanto, es suficiente encontrar todas las soluciones de solo las primeras r ecuaciones del sistema (3.1). Considere las primeras r ecuaciones del sistema (3.1), escribiéndolas en la forma
Si damos a las incógnitas xr + 1, ..., xn valores completamente arbitrarios cr + 1, ..., cn, entonces el sistema (1.19) se convertirá en un sistema cuadrático de r ecuaciones lineales para r incógnitas x 1, x 2, ..., х r, y el determinante de la matriz básica de este sistema es un menor básico distinto de cero de la matriz (3.2). En virtud de los resultados de la sección anterior, este sistema (3.19) tiene una solución única definida por las fórmulas de Cramer, es decir, para cr + 1 arbitrariamente elegido, ..., cn, existe una colección única r de números c 1, ..., cr, convirtiendo todas las ecuaciones del sistema (3.19) en identidades y definidas por las fórmulas de Cramer.
Para escribir esta solución única, acordamos denotar con el símbolo M j (di) el determinante obtenido del menor básico M de la matriz (3.2) reemplazando su columna j-ro con una columna de números d 1, d 2, ..., di, ..., dr (manteniendo todas las demás columnas M sin cambios). Luego, escribiendo la solución del sistema (3.19) usando las fórmulas de Cramer y usando la propiedad lineal del determinante, obtenemos
Las fórmulas (3.20) expresan los valores de las incógnitas xj = cj (j = 1, 2, ......, r) mediante los coeficientes de las incógnitas, términos libres y parámetros dados arbitrariamente con r + 1,. ..., con n.
Demostremos que las fórmulas (3.20) contienen cualquier solución del sistema (3.1)... De hecho, sea c (0) 1, c (0) 2, ..., c (0) r, c (0) r + 1, ..., c (0) n una solución arbitraria del sistema indicado . Entonces también es una solución al sistema (3.19). Pero del sistema (3.19) las cantidades c (0) 1, c (0) 2, ..., c (0) r, se determinan en términos de las cantidades c (0) r + 1, ..., c (0) n única y precisamente mediante las fórmulas de Cramer (3.20). Por lo tanto, para c r + 1 = c (0)
r + 1, ..., con norte = c (0)
norte
las fórmulas (3.20) nos dan solo la solución considerada c (0)
1
, C (0)
2
, ..., C (0)
r , C (0)
r + 1, ..., C (0)
norte .
Comentario. Si el rango r de las matrices principal y extendida del sistema (3.1) es igual al número de incógnitas n, entonces en este caso las relaciones (3.20) se convierten en fórmulas
determinar la solución única al sistema (3.1). Por lo tanto, el sistema (3.1) tiene una solución única (es decir, es definida) siempre que el rango r de sus matrices principal y extendida sea igual al número de incógnitas n (y sea menor o igual al número de ecuaciones m) .
Ejemplo. Encuentra todas las soluciones al sistema lineal.
Es fácil verificar que el rango de las matrices principal y extendida de este sistema es igual a dos (es decir, este sistema es consistente), y podemos asumir que el menor básico M está en la esquina superior izquierda de la matriz principal. , es decir 
... Pero luego, descartando las dos últimas ecuaciones y estableciendo arbitrariamente con 3 y con 4, obtenemos el sistema
x 1 - x 2 = 4 - do 3 + do 4,
x 1 + x 2 = 8 - 2c 3 - 3c 4,
del cual, en virtud de las fórmulas de Cramer, obtenemos los valores
x 1 = do 1 = 6 - 3/2 do 3 - do 4, x 2 = do 2 = 2 - 1/2 do 3 - 2c 4. (3,22)
Así, los cuatro números
(6 - 3/2 c 3 - c 4, 2 - 1/2 c 3 - 2c 4, c 3, c 4) (3.23)
al azar establecer valores c 3 y c 4 forman una solución del sistema (3.21), y la fila (3.23) contiene todas las soluciones de este sistema.
3. Propiedades del conjunto de soluciones de un sistema homogéneo. Consideremos ahora un sistema homogéneo de m ecuaciones lineales con n incógnitas (3.7), asumiendo, como antes, que la matriz (3.2) tiene un rango igual a r, y que el menor básico М está ubicado en la esquina superior izquierda de esta matriz. . Dado que esta vez todos los b i son iguales a cero, en lugar de las fórmulas (3.20) obtenemos las siguientes fórmulas:
expresando los valores de las incógnitas x j = c j (j = 1, 2, ..., r) en términos de los coeficientes de las incógnitas y valores dados arbitrariamente c r + 1, ..., c n. En virtud de lo probado en el párrafo anterior las fórmulas (3.24) contienen cualquier solución al sistema homogéneo (3.7).
Comprobemos ahora que la colección de todas las soluciones del sistema homogéneo (3.7) forma el espacio lineal.
Sea X 1 = (x (1) 1, x (1) 2, ..., x (1) n) y X 2 = (x (2) 1, x (2) 2, ..., x ( 2) n) son dos soluciones arbitrarias del sistema homogéneo (3.7), y λ es cualquier número real. Dado que cada solución del sistema homogéneo (3.7) es un elemento del espacio lineal А n de todas las colecciones ordenadas de n números, basta probar que cada una de las dos colecciones
X 1 + X 2 = (x (1) 1 + x (2) 1, ..., x (1) n + x (2) n)
λ X 1 = (λ x (1) 1, ..., λ x (1) n)
también es una solución al sistema homogéneo (3.7).
Considere cualquier ecuación del sistema (3.7), por ejemplo i-ésima ecuación, y sustituya en esta ecuación en lugar de los elementos desconocidos de los conjuntos especificados. Teniendo en cuenta que X 1 y X 2 son soluciones de un sistema homogéneo, tendremos
y esto significa que las colecciones X 1 + X 2 y λ X 1 son soluciones del sistema homogéneo (3.7).
Así, el conjunto de todas las soluciones del sistema homogéneo (3.7) forma un espacio lineal, que denotamos por R.
Encontremos la dimensión de este espacio R y construyamos una base en él.
Demostremos que bajo el supuesto de que el rango de la matriz del sistema homogéneo (3.7) es igual a r, el espacio lineal R de todas las soluciones del sistema homogéneo (3.7) es isomorfo al espacio lineal A n-r de todas las colecciones ordenadas (n - r) de números(el espacio n A m se introdujo en el Ejemplo 3, Sección 1, Sección 1, Capítulo 2).
Asociamos cada solución (c 1, ..., c r, c r + 1, ..., c n) del sistema homogéneo (3.7) con un elemento (c r + 1, ..., c n) del espacio A n-r Dado que los números c r + 1, ..., c n pueden elegirse arbitrariamente y para cada elección mediante las fórmulas (3.24) determinar de forma única la solución del sistema (3.7), la correspondencia que hemos establecido es doce y cincuenta y nueve de la noche... Además, tenga en cuenta que si los elementos c (1) r + 1, ..., c (1) n y c (2) r + 1, ..., c (2) n del espacio A n-r corresponden a los elementos (c (1) 1, ..., c (1) r, c (1) r + 1, ..., c (1) n) y (c (2) 1, ... , c (2) r, c (2) r + 1, ..., c (2) n) del espacio R, entonces las fórmulas (3.24) implican inmediatamente que el elemento (c (1) r + 1 + c (2) r + 1, ..., c (1) n + c (2) n) corresponde al elemento (c (1) 1 + c (2) 1, ..., c (1) r + c (2) r, c (1) r + 1 + c (2) r + 1, ..., c (1) n + c (2) n), y el elemento (λ c (1) r + 1, ..., λ c (1) n) para cualquier λ real corresponde un elemento (λ c (1) 1, ..., λ c (1) r, λ c (1) r + 1,. .., λ c (1) n). Esto prueba que la correspondencia que hemos establecido es un isomorfismo.
Así, el espacio lineal R de todas las soluciones del sistema homogéneo (3.7) con n incógnitas y el rango de la matriz principal igual a r es isomorfo al espacio A n-r y, por tanto, tiene dimensión n - r.
Cualquier conjunto de (n - r) soluciones linealmente independientes del sistema homogéneo (3.7) forma (según el teorema 2.5) una base en el espacio R de todas las soluciones y se denomina conjunto fundamental de soluciones del sistema homogéneo (3.7).
Para construir un conjunto fundamental de soluciones, puede ir desde cualquier base de espacio. A n-r... El conjunto de soluciones del sistema (3.7) correspondiente a esta base, por isomorfismo, será linealmente independiente y por tanto será un conjunto fundamental de soluciones.
Se distingue especialmente el conjunto fundamental de soluciones del sistema (3.7), correspondiente a la base más simple e 1 = (1, 0, 0, ..., 0), e 2 = (1, 1, 0, ..., 0), ..., е nr = (0, 0, 0, ..., 1) del espacio A n-r y llamado el conjunto fundamental normal de soluciones al sistema homogéneo (3.7).
Bajo los supuestos anteriores sobre el rango y la ubicación del menor básico, en virtud de las fórmulas (3.24), el conjunto fundamental normal de soluciones al sistema homogéneo (3.7) tiene la forma:
Por la definición de la base, cualquier solución X del sistema homogéneo (3.7) se puede representar en la forma
X = C 1 X 1 + C 2 X 2 + ... + C norte-r X norte-r, (3.26)
donde C 1, C 2, ..., C n-r son algunas constantes. Dado que la fórmula (3.26) contiene cualquier solución al sistema homogéneo (3.7), esta fórmula da una solución general al sistema homogéneo en consideración.
Ejemplo. Considere un sistema homogéneo de ecuaciones:
correspondiente al sistema no homogéneo (3.21) analizado en el ejemplo al final de la sección anterior. Allí descubrimos que el rango r de la matriz de este sistema es igual a dos, y tomamos como base el menor en la esquina superior izquierda de la matriz indicada.
Repitiendo el razonamiento al final de la sección anterior, obtenemos, en lugar de fórmulas (3.22), las relaciones
c 1 = - 3/2 c 3 - c 4, c 2 = - 1/2 c 3 - 2c 4,
válido para c 3 y c 4 elegidos arbitrariamente. Usando estas relaciones (asumiendo primero c 3 = 1, c 4 = 0, y luego c 3 = 0, c 4 = 1) obtenemos un conjunto fundamental normal de dos soluciones del sistema (3.27):
X 1 = (-3 / 2, -1 / 2,1,0), X 2 = (-1, -2, 0,1). (3,28)
donde C 1 y C 2 son constantes arbitrarias.
Para concluir este inciso, establecemos una conexión entre las soluciones del sistema lineal no homogéneo (3.1) y el sistema homogéneo correspondiente (3.7) (con los mismos coeficientes para las incógnitas). Probemos las siguientes dos afirmaciones.
1 °. La suma de cualquier solución del sistema no homogéneo (3.1) con cualquier solución del sistema homogéneo correspondiente (3.7) es una solución del sistema (3.1).
De hecho, si c 1, ..., cn es una solución del sistema (3.1), ad 1, ..., dn es una solución del sistema homogéneo correspondiente (3.7), entonces, sustituyendo en cualquier (por ejemplo, en la i-ésima) la ecuación del sistema (3.1) en lugar de los números desconocidos c 1 + d 1, ..., cn + dn, obtenemos
Q.E.D.
2 °. La diferencia de dos soluciones arbitrarias del sistema no homogéneo (3.1) es una solución del sistema homogéneo correspondiente (3.7).
De hecho, si c "1, ..., c" n y c "1, ..., c" n son dos soluciones arbitrarias del sistema (3.1), entonces, sustituyendo en cualquier ecuación (por ejemplo, en el i-ésimo) del sistema (3.7) en lugar de números desconocidos c "1 - c" 1, ..., c "n - c" n, obtenemos
Q.E.D.
De las declaraciones probadas se desprende que, encontrando una solución al sistema no homogéneo (3.1) y agregándola a cada solución del sistema homogéneo correspondiente (3.7), obtenemos todas las soluciones al sistema no homogéneo (3.1).
En otras palabras, la suma de una solución particular del sistema no homogéneo (3.1) y la solución general del sistema homogéneo correspondiente (3.7) da la solución general del sistema no homogéneo (3.1).
Como solución particular del sistema no homogéneo (3.1), es natural tomar su solución (en este caso, se supone, como se indicó anteriormente, que los rangos de las matrices principal y extendida del sistema (3.1) son iguales a ry que el menor básico está en la esquina superior izquierda de estas matrices)
que se obtendrá si todos los números c r + 1, ..., c n se igualan a cero en las fórmulas (3.20). Sumando esta solución particular con la solución general (3.26) del sistema homogéneo correspondiente, obtenemos la siguiente expresión para la solución general del sistema no homogéneo (3.1):
X = X 0 + C 1 X 1 + C 2 X 2 + ... + C norte-r X norte-r. (3,30)
En esta expresión, X 0 denota una solución particular (3.29), C 1, C 2, ..., C nr son constantes arbitrarias y X 1, X 2, ..., X nr son elementos del conjunto fundamental normal de soluciones (3.25) correspondiente sistema homogéneo.
Entonces, para el sistema no homogéneo (3.21) considerado al final de la sección anterior, la solución particular de la forma (3.29) es igual a X 0 = (6,2,0,0).
Sumando esta solución particular con la solución general (3.28) del sistema homogéneo correspondiente (3.27), obtenemos la siguiente solución general del sistema no homogéneo (3.21):
X = (6,2,0,0) + C 1 (-3 / 2, -1 / 2,1,0) + C 2 (-1, -2, 0,1). (3,31)
Aquí C 1 y C 2 son constantes arbitrarias.
4. Comentarios finales sobre la resolución de sistemas lineales. Métodos para resolver sistemas lineales desarrollados en los párrafos anteriores.
toparse con la necesidad de calcular el rango de la matriz y encontrar su menor básico. Una vez encontrado el menor básico, la solución se reduce a la técnica de cálculo de determinantes y al uso de fórmulas de Cramer.
Para calcular el rango de una matriz, puede usar la siguiente regla: al calcular el rango de una matriz, se debe pasar de menores de orden inferior a menores de orden superior; además, si ya se ha encontrado un menor M distinto de cero de orden k, entonces solo los menores de orden (k + 1) limítrofes(es decir, que contiene una M menor) este menor es M; si todos los menores limítrofes de orden (k + 1) son iguales a cero, el rango de la matriz es igual a k(de hecho, en el caso indicado, todas las filas (columnas) de la matriz pertenecen al casco lineal de sus k filas (columnas), en la intersección de las cuales hay una M menor, y la dimensión del casco lineal indicado es igual a k).
Indiquemos otra regla para calcular el rango de una matriz. Tenga en cuenta que con filas (columnas) de una matriz se puede producir tres operaciones elementales que no cambian el rango de esta matriz: 1) permutación de dos filas (o dos columnas), 2) multiplicación de una fila (o columna) por cualquier factor distinto de cero, 3) agregar a una fila (columna) una combinación lineal arbitraria de otras filas (columnas) (estas tres operaciones no cambian el rango de la matriz debido al hecho de que las operaciones 1) y 2) no cambian el número máximo de filas (columnas) linealmente independientes de la matriz, y la operación 3) tiene la propiedad de que el casco lineal de todas las filas (columnas) disponibles antes de esta operación, coincide con la envolvente lineal de todas las filas (columnas) obtenida después de esta operación).
Decimos que la matriz || a ij ||, que contiene m filas yn columnas, tiene diagonal forma, si todos sus elementos son iguales a cero, excepto a 11, a 22, .., a rr, donde r = min (m, n). El rango de tal matriz es obviamente r.
Asegurémonos de que por medio de tres operaciones elementales cualquier matriz
se puede reducir a forma diagonal(que nos permite calcular su rango).
De hecho, si todos los elementos de la matriz (3.31) son iguales a cero, entonces esta matriz ya se ha reducido a una forma diagonal. Si el mat-
Si la matriz (3.31) tiene elementos distintos de cero, entonces mediante la permutación de dos filas y dos columnas es posible lograr que el elemento a 11 sea distinto de cero. Después de eso, multiplicando la primera fila de la matriz por 11 -1, convertiremos el elemento a 11 en uno. Restando más de la columna j-ro de la matriz (para j = 2, 3, ..., n) la primera columna, multiplicada por i1, y luego restando de la i-ésima fila (para i = 2, 3 , ..., n) la primera fila, multiplicada por i1, obtenemos en lugar de (3.31) una matriz de la siguiente forma:
Realizando las operaciones ya descritas por nosotros con la matriz, tomada en el marco, y continuando actuando de manera similar, luego de un número finito de pasos obtendremos una matriz de forma diagonal.
Los métodos para resolver sistemas lineales descritos en los párrafos anteriores, que en última instancia utilizan el aparato de las fórmulas de Cramer, pueden conducir a grandes errores en el caso en que los valores de los coeficientes de las ecuaciones y términos libres se den aproximadamente o cuando estos valores Se redondean en el curso de los cálculos.
Esto se refiere principalmente al caso en que la matriz correspondiente al determinante principal (o menor básico) es mal condicionado(es decir, cuando cambios “pequeños” en los elementos de esta matriz corresponden a cambios “grandes” en los elementos de la matriz inversa). Naturalmente, en este caso, la solución al sistema lineal será inestable(es decir, cambios "grandes" en la solución corresponderán a cambios "pequeños" en los valores de los coeficientes de las ecuaciones y términos libres).
Estas circunstancias llevan a la necesidad de desarrollar tanto otros algoritmos teóricos (diferentes de las fórmulas de Cramer) para encontrar una solución, como métodos numéricos para resolver sistemas lineales.
En la Sección 4, Capítulo 4, nos familiarizaremos con por el método de regularización A.N. Tikhonov encontrar el llamado normal(es decir, la más cercana al origen) solución del sistema lineal.
El capítulo 6 proporcionará información básica sobre los llamados métodos iterativos soluciones de sistemas lineales que permiten resolver estos sistemas mediante sucesivas aproximaciones de incógnitas.
Un sistema de m ecuaciones lineales con n incógnitas llamado sistema de la forma
dónde a ij y b yo (I=1,…,metro; B=1,…,norte) Son algunos números conocidos, y x 1, ..., x n- desconocido. En la designación de los coeficientes a ij primer índice I denota el número de la ecuación, y el segundo j- el número de incógnitas en el que se encuentra este coeficiente.
Escribiremos los coeficientes para las incógnitas en forma de matriz.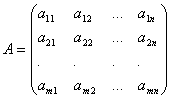 
, que llamaremos matriz del sistema.
Los números en el lado derecho de las ecuaciones. b 1, ..., b m son llamados miembros libres.
El agregado norte números c 1, ..., c n llamado decisión del sistema dado, si cada ecuación del sistema se convierte en igualdad después de la sustitución de números en ella c 1, ..., c n en lugar de las incógnitas correspondientes x 1, ..., x n.
Nuestra tarea será encontrar soluciones al sistema. En este caso, pueden surgir tres situaciones:
Un sistema de ecuaciones lineales que tiene al menos una solución se llama articulación... De lo contrario, es decir si el sistema no tiene soluciones, entonces se llama inconsistente.
Considere formas de encontrar soluciones al sistema.
MÉTODO MATRIZ PARA RESOLVER SISTEMAS DE ECUACIONES LINEALES
Las matrices permiten escribir de forma concisa un sistema de ecuaciones lineales. Sea un sistema de 3 ecuaciones con tres incógnitas:
Considere la matriz del sistema 
y columnas de matriz de términos desconocidos y libres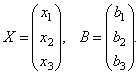 
Busquemos un trabajo
aquellos. como resultado del producto, obtenemos los lados izquierdos de las ecuaciones de este sistema. Luego, usando la definición de igualdad de matrices, este sistema se puede escribir en la forma
o mas corto A∙X = B.
Aquí matrices A y B son conocidos, y la matriz X desconocido. Ella también necesita ser encontrada, tk. sus elementos son la solución a este sistema. Esta ecuación se llama ecuación matricial.
Sea el determinante de la matriz distinto de cero | A| ≠ 0. Entonces, la ecuación matricial se resuelve de la siguiente manera. Multiplicamos ambos lados de la ecuación de la izquierda por la matriz A -1, la inversa de la matriz A:. En la medida en A -1 A = E y mi∙X = X, entonces obtenemos la solución de la ecuación matricial en la forma X = A -1 B .
Tenga en cuenta que dado que la matriz inversa se puede encontrar solo para matrices cuadradas, el método de la matriz se puede usar para resolver solo aquellos sistemas en los que el número de ecuaciones coincide con el número de incógnitas... Sin embargo, la representación matricial del sistema también es posible en el caso de que el número de ecuaciones no sea igual al número de incógnitas, entonces la matriz A no será cuadrado y, por lo tanto, es imposible encontrar una solución al sistema en la forma X = A -1 B.
Ejemplos. Resolver sistemas de ecuaciones.
REGLA DE CRAMER
Considere un sistema de 3 ecuaciones lineales con tres incógnitas:
Determinante de tercer orden correspondiente a la matriz del sistema, es decir compuesto por coeficientes con incógnitas,
llamado determinante del sistema.
Compongamos tres determinantes más de la siguiente manera: reemplace en el determinante D sucesivamente 1, 2 y 3 columnas con una columna de miembros libres
Entonces se puede probar el siguiente resultado.
Teorema (regla de Cramer). Si el determinante del sistema es Δ ≠ 0, entonces el sistema en consideración tiene una y solo una solución, y
Prueba... Entonces, consideremos un sistema de 3 ecuaciones con tres incógnitas. Multiplicamos la 1a ecuación del sistema por el complemento algebraico A 11 elemento a 11, 2da ecuación - en A 21 y tercero - en A 31:
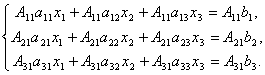
Agreguemos estas ecuaciones:
Veamos cada uno de los corchetes y el lado derecho de esta ecuación. Por el teorema sobre la expansión del determinante en términos de los elementos de la 1a columna
Del mismo modo, se puede demostrar que y.
Finalmente, es fácil ver que 
Así, obtenemos la igualdad :.
Por eso, .
Las igualdades y se derivan de manera similar, de donde se sigue la afirmación del teorema.
Por lo tanto, observamos que si el determinante del sistema es Δ ≠ 0, entonces el sistema tiene una solución única y viceversa. Si el determinante del sistema es igual a cero, entonces el sistema tiene un conjunto infinito de soluciones o no tiene soluciones, es decir, inconsistente.
Ejemplos. Resolver sistema de ecuaciones
MÉTODO GAUSS
Los métodos considerados anteriormente se pueden utilizar para resolver solo aquellos sistemas en los que el número de ecuaciones coincide con el número de incógnitas, y el determinante del sistema debe ser distinto de cero. El método de Gauss es más versátil y adecuado para sistemas con cualquier número de ecuaciones. Consiste en la eliminación sucesiva de incógnitas de las ecuaciones del sistema.
Considere nuevamente un sistema de tres ecuaciones con tres incógnitas:
.
Dejamos la primera ecuación sin cambios, y de la segunda y la tercera excluimos los términos que contienen x 1... Para hacer esto, dividimos la segunda ecuación por a 21 y multiplicar por - a 11 y luego agréguelo a la primera ecuación. De manera similar, dividimos la tercera ecuación en a 31 y multiplicar por - a 11, y luego agregue al primero. Como resultado, el sistema original tomará la forma:
Ahora excluimos de la última ecuación el término que contiene x 2... Para hacer esto, divida la tercera ecuación por, multiplique por y sume a la segunda. Entonces tendremos un sistema de ecuaciones:
Por tanto, a partir de la última ecuación es fácil encontrar x 3, luego de la segunda ecuación x 2 y finalmente desde el 1 - x 1.
Cuando se utiliza el método gaussiano, las ecuaciones se pueden intercambiar según sea necesario.
A menudo, en lugar de escribir un nuevo sistema de ecuaciones, se limitan a escribir la matriz extendida del sistema:
y luego llevarlo a una forma triangular o diagonal usando transformaciones elementales.
PARA transformaciones elementales Las matrices incluyen las siguientes transformaciones:
- reordenamiento de filas o columnas;
- multiplicar una cadena por un número distinto de cero;
- agregando otras líneas a una línea.
Ejemplos: Resolver sistemas de ecuaciones por el método de Gauss.
Por tanto, el sistema tiene un número infinito de soluciones.
Investigar un sistema de ecuaciones agebraicas lineales (SLAE) por compatibilidad significa averiguar si este sistema tiene soluciones o no. Bueno, si hay soluciones, indique cuántas de ellas.
Necesitamos información del tema "Sistema de ecuaciones algebraicas lineales. Términos básicos. Notación matricial". En particular, se necesitan conceptos como la matriz del sistema y la matriz extendida del sistema, ya que en ellos se basa la formulación del teorema de Kronecker-Capelli. Como es habitual, la matriz del sistema se indicará con la letra $ A $ y la matriz extendida del sistema con la letra $ \ widetilde (A) $.
Teorema de Kronecker-Capelli
El sistema de ecuaciones algebraicas lineales es consistente si y solo si el rango de la matriz del sistema es igual al rango de la matriz extendida del sistema, es decir, $ \ sonó A = \ sonó \ widetilde (A) $.
Permítanme recordarles que un sistema se llama conjunto si tiene al menos una solución. El teorema de Kronecker-Capelli dice lo siguiente: si $ \ rang A = \ rang \ widetilde (A) $, entonces hay una solución; si $ \ rang A \ neq \ rang \ widetilde (A) $, entonces este SLAE no tiene soluciones (inconsistente). La respuesta a la pregunta sobre el número de estas soluciones viene dada por un corolario del teorema de Kronecker-Capelli. En la formulación del corolario, se usa la letra $ n $, que es igual al número de variables del SLAE dado.
Corolario del teorema de Kronecker-Capelli
- Si $ \ rang A \ neq \ rang \ widetilde (A) $, entonces el SLAE es inconsistente (no tiene soluciones).
- Si $ \ sonó A = \ sonó \ widetilde (A)< n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
- Si $ \ rang A = \ rang \ widetilde (A) = n $, entonces el SLAE es definido (tiene exactamente una solución).
Tenga en cuenta que el teorema anterior y su corolario no indican cómo encontrar la solución al SLAE. Con su ayuda, solo se puede averiguar si estas soluciones existen o no, y si existen, entonces cuántas.
Ejemplo 1
Explore SLAE $ \ left \ (\ begin (alineado) & -3x_1 + 9x_2-7x_3 = 17; \\ & -x_1 + 2x_2-4x_3 = 9; \\ & 4x_1-2x_2 + 19x_3 = -42. \ End (alineado ) \ right. $ para compatibilidad Si el SLAE es compatible, indique el número de soluciones.
Para averiguar la existencia de soluciones para un SLAE dado, usamos el teorema de Kronecker-Capelli. Necesitamos la matriz del sistema $ A $ y la matriz extendida del sistema $ \ widetilde (A) $, las escribimos:
$$ A = \ left (\ begin (array) (ccc) -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \ end (array) \ right); \; \ widetilde (A) = \ left (\ begin (array) (ccc | c) -3 & 9 & -7 & 17 \\ -1 & 2 & -4 & 9 \\ 4 & -2 & 19 & -42 \ end (matriz) \ right). $$
Encuentra $ \ rang A $ y $ \ rang \ widetilde (A) $. Hay muchas formas de hacer esto, algunas de las cuales se enumeran en la sección Rango de matriz. Por lo general, se utilizan dos métodos para estudiar dichos sistemas: "Cálculo del rango de una matriz por definición" o "Cálculo del rango de una matriz mediante el método de transformaciones elementales".
Método número 1. Cálculo de rangos por definición.
Por definición, el rango es el orden más alto de la matriz de menores, entre los cuales hay al menos uno distinto de cero. Por lo general, el estudio comienza con menores de primer orden, pero aquí es más conveniente comenzar a calcular inmediatamente el menor de tercer orden de la matriz $ A $. Los elementos del tercer orden menor están en la intersección de tres filas y tres columnas de la matriz considerada. Dado que la matriz $ A $ contiene solo 3 filas y 3 columnas, el tercer orden menor de la matriz $ A $ es el determinante de la matriz $ A $, es decir $ \ Delta A $. Para calcular el determinante, apliquemos la fórmula # 2 del tema "Fórmulas para calcular determinantes de segundo y tercer orden":
$$ \ Delta A = \ left | \ begin (matriz) (ccc) -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \ end (matriz) \ right | = -21. $$
Entonces, hay un menor de tercer orden de la matriz $ A $, que no es igual a cero. Es imposible componer un menor de cuarto orden, ya que requiere 4 filas y 4 columnas, y en la matriz $ A $ solo hay 3 filas y 3 columnas. Entonces, el orden más alto de los menores de la matriz $ A $, entre los cuales hay al menos uno distinto de cero, es igual a 3. Por lo tanto, $ \ rang A = 3 $.
También necesitamos encontrar $ \ rang \ widetilde (A) $. Echemos un vistazo a la estructura de la matriz $ \ widetilde (A) $. La matriz $ \ widetilde (A) $ contiene los elementos de la matriz $ A $, y descubrimos que $ \ Delta A \ neq 0 $. Por lo tanto, la matriz $ \ widetilde (A) $ tiene un menor de tercer orden que no es cero. No podemos componer los menores de cuarto orden de la matriz $ \ widetilde (A) $, por lo que concluimos: $ \ rang \ widetilde (A) = 3 $.
Dado que $ \ rang A = \ rang \ widetilde (A) $, de acuerdo con el teorema de Kronecker-Capelli, el sistema es consistente, es decir, tiene una solución (al menos una). Para indicar el número de soluciones, tengamos en cuenta que nuestro SLAE contiene 3 incógnitas: $ x_1 $, $ x_2 $ y $ x_3 $. Dado que el número de incógnitas es $ n = 3 $, concluimos: $ \ rang A = \ rang \ widetilde (A) = n $, por lo tanto, de acuerdo con el corolario del teorema de Kronecker-Capelli, el sistema es definido, es decir, tiene una sola solución.
El problema ha sido resuelto. ¿Cuáles son las desventajas y ventajas de este método? Primero, hablemos de los pros. Primero, solo necesitábamos encontrar un determinante. Después de eso, inmediatamente llegamos a una conclusión sobre la cantidad de soluciones. Por lo general, en los cálculos estándar estándar, se dan sistemas de ecuaciones que contienen tres incógnitas y tienen una solución única. Para tales sistemas este método incluso es muy conveniente, porque sabemos de antemano que hay una solución (de lo contrario no habría ejemplo en un cálculo típico). Aquellos. solo tenemos que mostrar la existencia de una solución de lo más manera rápida... En segundo lugar, el valor calculado del determinante de la matriz del sistema (es decir, $ \ Delta A $) será útil después: cuando comencemos a resolver el sistema dado por el método de Cramer o usando la matriz inversa.
Sin embargo, el método de calcular el rango es por definición indeseable si la matriz del sistema $ A $ es rectangular. En este caso, es mejor utilizar el segundo método, que se discutirá a continuación. Además, si $ \ Delta A = 0 $, entonces no podemos decir nada sobre el número de soluciones de un SLAE no homogéneo dado. Quizás SLAE tenga un número infinito de soluciones, o quizás ninguna. Si $ \ Delta A = 0 $, entonces se requiere investigación adicional, que a menudo es engorrosa.
Resumiendo lo dicho, observo que el primer método es bueno para aquellos SLAE en los que la matriz del sistema es cuadrada. En este caso, el SLAE en sí mismo contiene tres o cuatro incógnitas y se toma de cálculos típicos estándar o trabajos de control.
Método número 2. Cálculo del rango por el método de transformaciones elementales.
Este método se describe en detalle en el tema relacionado. Comenzaremos a calcular el rango de la matriz $ \ widetilde (A) $. ¿Por qué exactamente matrices $ \ widetilde (A) $ y no $ A $? El hecho es que la matriz $ A $ es parte de la matriz $ \ widetilde (A) $, por lo tanto, calculando el rango de la matriz $ \ widetilde (A) $, encontraremos simultáneamente el rango de la matriz $ A PS
\ begin (alineado) & \ widetilde (A) = \ left (\ begin (matriz) (ccc | c) -3 & 9 & -7 & 17 \\ -1 & 2 & -4 & 9 \\ 4 & - 2 & 19 & -42 \ end (arreglo) \ right) \ rightarrow \ left | \ text (intercambia la primera y la segunda línea) \ right | \ rightarrow \\ & \ rightarrow \ left (\ begin (array) (ccc | c) -1 & 2 & -4 & 9 \\ -3 & 9 & -7 & 17 \\ 4 & -2 & 19 & - 42 \ end (matriz) \ right) \ begin (matriz) (l) \ phantom (0) \\ r_2-3r_1 \\ r_3 + 4r_1 \ end (matriz) \ rightarrow \ left (\ begin (matriz) (ccc | c) -1 & 2 & -4 & 9 \\ 0 & 3 & 5 & -10 \\ 0 & 6 & 3 & -6 \ end (array) \ right) \ begin (array) (l) \ phantom ( 0) \\ \ phantom (0) \\ r_3-2r_2 \ end (matriz) \ rightarrow \\ & \ rightarrow \ left (\ begin (matriz) (ccc | c) -1 & 2 & -4 & 9 \\ 0 y 3 y 5 y -10 \\ 0 y 0 y -7 y 14 \ end (matriz) \ derecha) \ end (alineado)
Hemos transformado la matriz $ \ widetilde (A) $ en una forma escalonada. La matriz de pasos resultante tiene tres filas distintas de cero, por lo que su rango es 3. En consecuencia, el rango de la matriz $ \ widetilde (A) $ es 3, es decir, $ \ sonó \ widetilde (A) = 3 $. Haciendo transformaciones con los elementos de la matriz $ \ widetilde (A) $, transformamos simultáneamente los elementos de la matriz $ A $, ubicados hasta la línea. La matriz $ A $ también se escalona: $ \ left (\ begin (array) (ccc) -1 & 2 & -4 \\ 0 & 3 & 5 \\ 0 & 0 & -7 \ end (array) \ right) PS Conclusión: el rango de la matriz $ A $ también es igual a 3, es decir $ \ sonó A = 3 $.
Dado que $ \ rang A = \ rang \ widetilde (A) $, de acuerdo con el teorema de Kronecker-Capelli, el sistema es consistente, es decir, tiene una solución. Para indicar el número de soluciones, tengamos en cuenta que nuestro SLAE contiene 3 incógnitas: $ x_1 $, $ x_2 $ y $ x_3 $. Dado que el número de incógnitas es $ n = 3 $, concluimos: $ \ rang A = \ rang \ widetilde (A) = n $, por lo tanto, de acuerdo con el corolario del teorema de Kronecker-Capelli, el sistema está definido, es decir tiene una sola solución.
¿Cuáles son las ventajas del segundo método? La principal ventaja es su versatilidad. No nos importa en absoluto si la matriz del sistema es cuadrada o no. Además, realizamos transformaciones del curso directo del método de Gauss. Solo quedan un par de acciones y podríamos obtener la solución de este SLAE. Para ser honesto, me gusta más el segundo método que el primero, pero la elección es cuestión de gustos.
Respuesta: El SLAE dado es coherente y está definido.
Ejemplo No. 2
Explore SLAE $ \ left \ (\ begin (alineado) & x_1-x_2 + 2x_3 = -1; \\ & -x_1 + 2x_2-3x_3 = 3; \\ & 2x_1-x_2 + 3x_3 = 2; \\ & 3x_1- 2x_2 + 5x_3 = 1; \\ & 2x_1-3x_2 + 5x_3 = -4. \ End (alineado) \ right. $ Por compatibilidad.
Encontraremos los rangos de la matriz del sistema y la matriz extendida del sistema por el método de transformaciones elementales. Matriz de sistema extendida: $ \ widetilde (A) = \ left (\ begin (array) (ccc | c) 1 & -1 & 2 & -1 \\ -1 & 2 & -3 & 3 \\ 2 & -1 & 3 & 2 \\ 3 & -2 & 5 & 1 \\ 2 & -3 & 5 & -4 \ end (array) \ right) $. Encuentre los rangos requeridos transformando la matriz extendida del sistema:
$$ \ left (\ begin (array) (ccc | c) 1 & -1 & 2 & -1 \\ -1 & 2 & -3 & 3 \\ 2 & -3 & 5 & -4 \\ 3 & -2 & 5 & 1 \\ 2 & -1 & 3 & 2 \ end (arreglo) \ right) \ begin (arreglo) (l) \ phantom (0) \\ r_2 + r_1 \\ r_3-2r_1 \\ r_4 -3r_1 \\ r_5-2r_1 \ end (matriz) \ rightarrow \ left (\ begin (matriz) (ccc | c) 1 & -1 & 2 & -1 \\ 0 & 1 & -1 & 2 \\ 0 & -1 & 1 & -2 \\ 0 & 1 & -1 & 4 \\ 0 & 1 & -1 & 4 \ end (arreglo) \ right) \ begin (arreglo) (l) \ phantom (0) \\ \ phantom (0) \\ r_3-r_2 \\ r_4-r_2 \\ r_5 + r_2 \ end (matriz) \ rightarrow \\ $$ $$ \ rightarrow \ left (\ begin (matriz) (ccc | c) 1 & -1 & 2 & -1 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \ end (matriz) \ derecha) \ begin (matriz) (l) \ phantom (0) \\\ phantom (0) \\\ phantom (0) \\ r_4-r_3 \\\ phantom (0) \ end (matriz) \ rightarrow \ left (\ begin (matriz) (ccc | c) 1 & -1 & 2 & -1 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \ end (matriz) \ right) $$
La matriz del sistema expandida se escalona. El rango de una matriz escalonada es igual al número de sus filas distintas de cero, por lo tanto $ \ rang \ widetilde (A) = 3 $. La matriz $ A $ (al punto) también se reduce a una forma escalonada, y su rango es igual a 2, $ \ rang (A) = 2 $.
Dado que $ \ rang A \ neq \ rang \ widetilde (A) $, de acuerdo con el teorema de Kronecker-Capelli, el sistema es inconsistente (es decir, no tiene soluciones).
Respuesta: El sistema es inconsistente.
Ejemplo No. 3
Explore SLAE $ \ left \ (\ begin (alineado) & 2x_1 + 7x_3-5x_4 + 11x_5 = 42; \\ & x_1-2x_2 + 3x_3 + 2x_5 = 17; \\ & -3x_1 + 9x_2-11x_3-7x_5 = -64 ; \\ & -5x_1 + 17x_2-16x_3-5x_4-4x_5 = -90; \\ & 7x_1-17x_2 + 23x_3 + 15x_5 = 132. \ End (alineado) \ right. $ Por compatibilidad.
Traemos la matriz extendida del sistema a una forma escalonada:
$$ \ left (\ begin (array) (ccccc | c) 2 & 0 & 7 & -5 & 11 & 42 \\ 1 & -2 & 3 & 0 & 2 & 17 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \ end (array) \ right) \ overset (r_1 \ leftrightarrow (r_3)) (\ rightarrow) $$ $$ \ rightarrow \ left (\ begin (array) (ccccc | c) 1 & -2 & 3 & 0 & 2 & 17 \\ 2 & 0 & 7 & -5 & 11 & 42 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \ end (matriz) \ right) \ begin (matriz) (l) \ phantom (0) \\ r_2-2r_1 \\ r_3 + 3r_1 \\ r_4 + 5r_1 \\ r_5-7r_1 \ end ( matriz) \ flecha derecha \ izquierda (\ begin (matriz) (ccccc | c) 1 & -2 & 3 & 0 & 2 & 17 \\ 0 & 4 & 1 & -5 & 7 & 8 \\ 0 & 3 & - 2 & 0 & -1 & -13 \\ 0 & 7 & -1 & -5 & 6 & -5 \\ 0 & -3 & 2 & 0 & 1 & 13 \ end (array) \ right) \ begin ( matriz) (l) \ phantom (0) \\ \ phantom (0) \\ 4r_3 + 3r_2 \\ 4r_4-7r_2 \\ 4r_5 + 3r_2 \ end (matriz) \ rightarrow $$ \ rightarrow \ left (\ begin (matriz ) (ccccc | c) 1 & -2 & 3 & 0 & 2 & 17 \\ 0 & 4 & 1 & -5 & 7 & 8 \\ 0 & 0 & -11 & 15 & -25 & -76 \\ 0 y 0 y -11 y 15 y -25 y -76 \\ 0 & 0 & 11 & -15 & 25 & 76 \ end (arreglo) \ right) \ begin (arreglo) (l) \ phantom (0) \\ \ phantom (0) \\\ phantom (0) \\ r_4 -r_3 \\ r_5 + r_2 \ end (matriz) \ rightarrow \ left (\ begin (matriz) (ccccc | c) 1 & -2 & 3 & 0 & 2 & 17 \\ 0 & 4 & 1 & -5 & 7 & 8 \\ 0 & 0 & -11 & 15 & -25 & -76 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \ end (matriz) \ derecha) $$
Hemos llevado la matriz del sistema extendida y la propia matriz del sistema a una forma escalonada. El rango de la matriz extendida del sistema es tres, el rango de la matriz del sistema también es tres. Dado que el sistema contiene $ n = 5 $ incógnitas, es decir $ \ rang \ widetilde (A) = \ rang (A) \ lt (n) $, entonces, de acuerdo con el corolario del teorema de Kronecker-Capelli, este sistema no está definido, es decir, tiene un número infinito de soluciones.
Respuesta: el sistema no está definido.
En la segunda parte analizaremos ejemplos que suelen incluirse en cálculos o pruebas típicas en matemáticas superiores: un estudio de compatibilidad y la solución de un SLAE, en función de los valores de los parámetros incluidos en el mismo.
Ejemplo 1... Encuentre una solución general y alguna solución particular para el sistemaSolución realizamos con la ayuda de una calculadora. Escribamos las matrices extendidas y básicas: 
La línea de puntos separa la matriz principal A. Arriba escribimos los sistemas desconocidos, teniendo en cuenta la posible reordenación de los términos en las ecuaciones del sistema. Determinando el rango de la matriz extendida, encontramos simultáneamente el rango y el principal. En la matriz B, la primera y la segunda columnas son proporcionales. De las dos columnas proporcionales, solo una puede caer en la menor básica, por lo que trasladamos, por ejemplo, la primera columna detrás de la línea discontinua con el signo opuesto. Para el sistema, esto significa mover los términos de x 1 al lado derecho de las ecuaciones. 
Llevemos la matriz a una forma triangular. Trabajaremos solo con filas, ya que multiplicar una fila de una matriz por un número que no sea cero y sumar a otra fila para el sistema significa multiplicar la ecuación por el mismo número y sumarla a otra ecuación, lo que no cambia la solución de el sistema. Trabajamos con la primera fila: multiplicamos la primera fila de la matriz por (-3) y sumamos a la segunda y tercera filas sucesivamente. Luego multiplicamos la primera línea por (-2) y la sumamos a la cuarta. 
La segunda y tercera líneas son proporcionales, por lo tanto, una de ellas, por ejemplo la segunda, se puede tachar. Esto equivale a borrar la segunda ecuación del sistema, ya que es consecuencia de la tercera. 
Ahora estamos trabajando con la segunda línea: multiplícala por (-1) y suma a la tercera. 
El menor punteado tiene el orden más alto (de los posibles menores) y es distinto de cero (es igual al producto de los elementos en la diagonal principal), y este menor pertenece tanto a la matriz principal como a la extendida, por lo tanto, rangA = sonóB = 3.
Menor 
es básico. Incluye los coeficientes para las incógnitas x 2, x 3, x 4, lo que significa que las incógnitas x 2, x 3, x 4 son dependientes y x 1, x 5 son libres.
Transformamos la matriz, dejando solo la base menor a la izquierda (que corresponde al punto 4 del algoritmo de solución anterior). 
El sistema con los coeficientes de esta matriz es equivalente al sistema original y tiene la forma
x 4 = 3-4x 5, x 3 = 3-4x 5 -2x 4 = 3-4x 5-6 + 8x 5 = -3 + 4x 5
x 2 = x 3 + 2x 4 -2 + 2x 1 + 3x 5 = -3 + 4x 5 + 6-8x 5-2 + 2x 1 + 3x 5 = 1 + 2x 1 -x 5
Obtuvimos las razones que expresan las variables dependientes x 2, x 3, x 4 a través de x 1 y x 5 libres, es decir, encontramos una solución general:
Al asignar cualquier valor a las incógnitas libres, obtenemos tantas soluciones particulares como queramos. Busquemos dos soluciones particulares:
1) sea x 1 = x 5 = 0, luego x 2 = 1, x 3 = -3, x 4 = 3;
2) ponga x 1 = 1, x 5 = -1, luego x 2 = 4, x 3 = -7, x 4 = 7.
Por lo tanto, encontramos dos soluciones: (0.1, -3.3.0) - una solución, (1.4, -7.7, -1) - otra solución.
Ejemplo 2... Investigar la compatibilidad, encontrar una solución general y una particular al sistema 
Solución... Reorganizamos la primera y la segunda ecuación para que tengan unidad en la primera ecuación y escribimos la matriz B. 
Obtenemos ceros en la cuarta columna, operando en la primera fila: 
Ahora obtenemos los ceros en la tercera columna usando la segunda fila: 
La tercera y cuarta líneas son proporcionales, por lo que una de ellas se puede tachar sin cambiar el rango:
Multiplicamos la tercera fila por (–2) y sumamos a la cuarta: 
Vemos que los rangos de las matrices principal y extendida son iguales a 4, y el rango coincide con el número de incógnitas, por lo tanto, el sistema tiene una solución única:
-x 1 = -3 → x 1 = 3; x 2 = 3-x 1 → x 2 = 0; x 3 = 1-2x 1 → x 3 = 5.
x 4 = 10 - 3x 1 - 3x 2 - 2x 3 = 11.
Ejemplo 3... Examine el sistema para ver si es compatible y encuentre una solución, si existe. 
Solución... Componemos una matriz extendida del sistema. 
Reorganizamos las dos primeras ecuaciones para que haya 1 en la esquina superior izquierda:
Multiplicando la primera línea por (-1), agréguela a la tercera: 
Multiplica la segunda fila por (-2) y suma a la tercera: 
El sistema es inconsistente, ya que en la matriz principal obtenemos una fila formada por ceros, que se tacha cuando se encuentra el rango, y en la matriz extendida quedará la última fila, es decir, r B> r A.
Ejercicio... Investigue la consistencia de este sistema de ecuaciones y resuélvalo usando cálculo matricial.
Solución
Ejemplo... Demuestre la compatibilidad del sistema de ecuaciones lineales y resuélvalo de dos formas: 1) el método de Gauss; 2) Método de Cramer. (ingrese la respuesta en el formulario: x1, x2, x3)
Solución: doc: doc: xls
Respuesta: 2,-1,3.
Ejemplo... Se da un sistema de ecuaciones lineales. Demuestra su compatibilidad. Encuentre una solución general para el sistema y una solución particular.
Solución
Respuesta: x 3 = - 1 + x 4 + x 5; x 2 = 1 - x 4; x 1 = 2 + x 4 - 3x 5
Ejercicio... Encuentre soluciones generales y específicas para cada sistema.
Solución. Investiguemos este sistema utilizando el teorema de Kronecker-Capelli.
Escribamos las matrices extendidas y básicas:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Aquí la matriz A está en negrita.
Llevemos la matriz a una forma triangular. Trabajaremos solo con filas, ya que multiplicar una fila de una matriz por un número que no sea cero y sumar a otra fila para el sistema significa multiplicar la ecuación por el mismo número y sumarla a otra ecuación, lo que no cambia la solución de el sistema.
Multiplica la primera fila por (3). Multiplica la segunda fila por (-1). Agreguemos la segunda línea a la primera:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Multiplica la segunda fila por (2). Multiplica la tercera fila por (-3). Agreguemos la tercera línea a la segunda:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Multiplica la segunda fila por (-1). Agreguemos la segunda línea a la primera:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
El menor resaltado tiene el orden más alto (de los posibles menores) y es distinto de cero (es igual al producto de los elementos en la diagonal inversa), y este menor pertenece tanto a la matriz principal como a la extendida, por lo tanto, sonó ( A) = rang (B) = 3. Dado que el rango de la matriz principal es igual al rango de la extendida, entonces el sistema es una articulación.
Este menor es básico. Incluye los coeficientes para las incógnitas x 1, x 2, x 3, lo que significa que las incógnitas x 1, x 2, x 3 son dependientes (básicas) y x 4, x 5 son libres.
Transformamos la matriz, dejando solo la base menor a la izquierda.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
27x 3 =
- x 2 + 13x 3 = - 1 + 3x 4 - 6x 5
2x 1 + 3x 2 - 3x 3 = 1 - 3x 4 + 2x 5
Usando el método de eliminación de incógnitas, encontramos:
Obtuvimos relaciones que expresan las variables dependientes x 1, x 2, x 3 a través de x 4, x 5 libres, es decir, encontramos decisión común:
x 3 = 0
x 2 = 1 - 3x 4 + 6x 5
x 1 = - 1 + 3x 4 - 8x 5
indefinido ya que tiene más de una solución.
Ejercicio... Resuelve el sistema de ecuaciones.
Respuesta: x 2 = 2 - 1,67x 3 + 0,67x 4
x 1 = 5 - 3,67x 3 + 0,67x 4
Al asignar cualquier valor a las incógnitas libres, obtenemos tantas soluciones particulares como queramos. El sistema es indefinido
