Вершины многоугольника это. Вершина многоугольника это Что такое вершины многоугольника

Многоугольник. Вершины, углы, стороны и диагонали
многоугольника. Периметр многоугольника.
Простой многоугольник. Выпуклый многоугольник.
Сумма внутренних углов выпуклого многоугольника.

Плоская фигура, образованная замкнутой цепочкой отрезков, называется многоугольником . В зависимости от количества углов многоугольник может быть треугольником , четырёхугольником , пятиугольником , шестиугольником и т.д. На рис.17 показан шестиугольник ABCDEF. Точки А, В, C, D, E, F – вершины

Многоугольника ; углы A , B , C , D, E , F – углы многоугольника ; отрезки AC, AD, BE и т.д. - диагонали ; AB, BC, CD, DE, EF, FA – стороны многоугольника ; сумма длин сторон AB + BC + … + FA называется периметром и обозначается p (иногда обозначают – 2p , тогда p – полупериметр ). В элементарной геометрии рассматриваются только простые многоугольники, контуры которых не имеют самопересечений, как показано на рис.18. Если все диагонали лежат внутри многоугольника, он называется выпуклым . Шестиугольник на рис.17 выпуклый; пятиугольник ABCDE на рис.19 не выпуклый, так как его диагональ AD лежит снаружи. Сумма внутренних углов выпуклого многоугольника равна 180º ( n – 2), где n - число углов (или сторон) многоугольника.

Параллелограмм. Свойства и признаки параллелограмма.

Прямоугольник. Основные свойства прямоугольника. Ромб.

Квадрат. Трапеция. Средние линии трапеции и треугольника.

Параллелограмм (ABCD, рис.32) – это четырёхугольник, противоположные стороны которого попарно параллельны.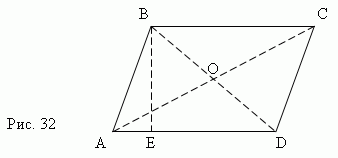

Любые две противоположные стороны параллелограмма называются его основаниями , а расстояние между ними – высотой (BE, рис.32).

Свойства параллелограмма.

1. Противоположные стороны параллелограмма равны (AB = CD, AD = BC).

2. Противоположные углы параллелограмма равны ( A = C, B = D).

3. Диагонали параллелограмма делятся в точке их пересечения пополам (AO = OC, BO = OD).

4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его четырёх сторон :

AC² + BD² = AB² + BC² + CD² + AD² .

Признаки параллелограмма.

Четырёхугольник является параллелограммом, если выполняется одно из следующих условий:

1. Противоположные стороны попарно равны (AB = CD, AD = BC).

2. Противоположные углы попарно равны ( A = C, B = D).

3. Две противоположные стороны равны и параллельны (AB = CD, AB || CD).

4. Диагонали делятся в точке их пересечения пополам (AO = OC, BO = OD).

Прямоугольник.

Br />
Если один из углов параллелограмма прямой, то все остальные углы также прямые (почему?). Такой параллелограмм называется прямоугольником (рис.33) .

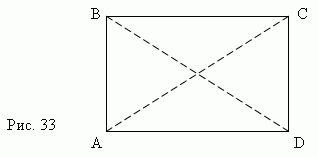
Основные свойства прямоугольника.

Стороны прямоугольника являются одновременно его высотами.

Диагонали прямоугольника равны: AC = BD.

Квадрат диагонали прямоугольника равен сумме квадратов его сторон (см. выше теорему Пифагора):

AC 2 = AD 2 + DC 2 .

Ромб. Если все стороны параллелограмма равны, то этот параллелограмм называется ромбом (рис.34) .

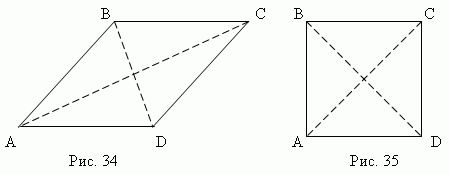
Диагонали ромба взаимно перпендикулярны (AC BD) и делят их углы пополам (DCA = BCA, ABD = CBD и т.д.).

Квадрат – это параллелограмм с прямыми углами и равными сторонами (рис.35). Квадрат является частным случаем прямоугольника и ромба одновременно; поэтому он обладает всеми их вышеперечисленными свойствами.

R />
Трапеция - это четырёхугольник, у которого е противоположные сто роны параллельны (рис.36).

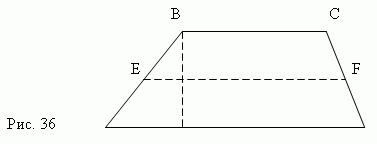
Здесь AD || BC. Параллельные стороны называются основаниями трапеции, а две другие (AB и CD) – боковыми сторонами. Расстояние между основаниями (BM) есть высота. Отрезок EF, соединяющий средние точки E и F

Боковых сторон, называется средней линией трапеции. Средняя линия трапеции равна полусумме оснований:

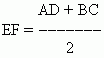
и параллельна им: EF || AD и EF || BC.

Трапеция с равными боковыми сторонами (AB = CD) называется равнобоч ной трапецией. В равнобочной трапеции углы при каждом основании равны ( A = D, B = C).

Параллелограмм может рассматриваться как частный случай трапеции.

Средняя линия треугольника – это отрезок, соединяющий средние точки боковых сторон треугольника. Средняя линия треугольника равна половине го основания и параллельна ему. о свойство вытекает из предыдущего

Пункта, так как треугольник может рассматриваться как случай вырождения трапеции, когда одно из её оснований превращается в точку.

Вписанный в круг многоугольник .

Описанный около круга многоугольник .

Описанный около многоугольника круг.

Вписанный в многоугольник круг.

Радиус вписанного в треугольник круга .

Радиус описанного около треугольника круга .
Правильный многоугольник.

Центр и апофема правильного многоугольника.
Соотношения сторон и радиусов правильных многоугольников .

Вписанным в круг называется многоугольник, вершины которого расположены на окружности рис.54). Описанным около круга называется ногоугольник, стороны которого являются касательными к окружности

(рис.55).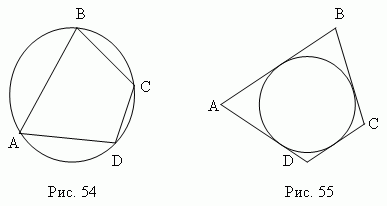

Соответственно, окружность, проходящая через вершины многоугольника (рис.54), называется описанной около многоугольника ; окружность, для которой стороны многоугольника являются касательными (рис.55) , на зывается вписанной в многоугольник. Для произвольного многоугольника невозможно вписать в него и описать около него окружность . Для треуголь ника это всегда возможно.

Радиус r вписанного круга выражается через стороны a, b, c треугольника:

Радиус R описанного круга выражается формулой: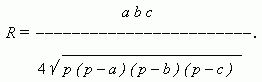

В четырёхугольник можно вписать окружность, если суммы его противоположных сторон равны. Для параллелограммов это возможно только для ромба (квадрата). Центр вписанного круга расположен в точке пересечения диагоналей. Около четырёхугольника можно описать круг, если сумма его противоположных углов равна 180º. Для параллелограммов это возможно только для прямоугольника (квадрата). Центр описанного круга лежит в точке пересечения диагоналей. Вокруг трапеции можно описать круг, еслитолько она равнобочная.r />

Правильный многоугольник то многоугольник с равными сторонами и углами.

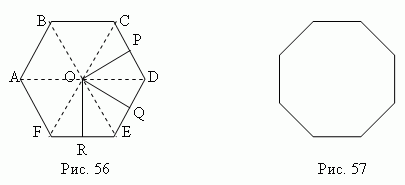
На рис.56 показан правильный шестиугольник, а на рис.57 – правильный восьмиугольник. Правильный четырёхугольник – это квадрат; правильный треугольник – равносторонний треугольник. Каждый угол правильного многоугольника равен 180º (n – 2) / n ,где n – число его углов. Внутри правильного многоугольника существует точка O (рис. 56), равноудалённая от всех его вершин (OA = OB = OC = … = OF), которая называется центром правильного многоугольника. Центр правильного многоугольника также равноудалён от всех его сторон (OP = OQ = OR = …). Отрезки OP, OQ, OR, … называются апофемами ; отрезки OA, OB, OC, …– радиусы правильного многоугольника. В правильный многоугольник можно вписать окружность и около него можно описать окружность. Центры вписанной и описанной окружностей совпадают с центром правильного многоугольника. Радиус описанного круга - это радиус правильного многоугольника, a радиус вписанного круга - его апофема. Соотношения сторон и радиусов правильных многоугольников:

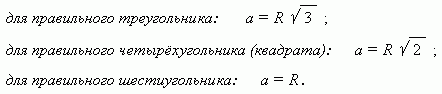
Для большинства правильных многоугольников невозможно выразить посредством алгебраической формулы соотношение между их сторонами и радиусами.

П р и м е р. Можно ли вырезать квадрат со стороной 30 см из круга

Диаметром 40 см?

Р е ш е н и е. Наибольший квадрат, заключённый в круг, есть вписанный

Квадрат. В соответствии с вышеприведенной формулой его

Сторона равна:

Следовательно, квадрат со стороной 30 см невозможно вырезать

Из круга диаметром 40 см.

Вершинами многоугольника, а отрезки сторонами многоугольника. Вершины многоугольника - страница №1/1

Геометрия 8 класс К.К.Кургинян Часть-1* (со звездочкой).
Многоугольник.

Определение: Многоугольник - это геометрическая фигура, которая состоит из плоской, замкнутой ломаной без самопересечений. Вершины ломаной называются вершинами многоугольника, а отрезки - сторонами многоугольника.

Вершины многоугольника называются соседними , если они являются концами одной из его сторон. Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями .

Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол это разность между 180° и внутренним углом, он может принимать значения от -180° до 180°. Сумма внешних углов многоугольника 360°.

Выпуклый многоугольник.
Многоугольник называется выпуклым если:
Определение I - для любых двух точек внутри него соединяющий их отрезок полностью лежит в нём.

Определение II - каждый внутренний угол меньше 180° .

Определение III - все его диагонали полностью лежат внутри него.

Определение IV – он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Сумма углов n -угольника.
Сумма углов выпуклого n-угольника равна (n-2)∙180°.
Сумма углов невыпуклого n-угольника также равна (n-2)∙180°. (Доказательство аналогично, но использует в дополнение лемму о том, что любой многоугольник может быть разрезан диагоналями на треугольники).
Число диагоналей n -угольника.*

Теорема: Число диагоналей всякого n-угольника равно n(n-3)2.

Доказательство: Пусть n - число вершин многоугольника, вычислим p- число возможных разных диагоналей. Каждая вершина соединена диагоналями со всеми другими вершинами, кроме двух соседних и, естественно, себя самой. Таким образом, из одной вершины можно провести n-3 диагонали; перемножим это на число вершин (n-3)∙n, однако, мы посчитали каждую диагональ дважды (по разу для каждого конца, следовательно, надо разделить на 2) - отсюда, p= n(n-3)2.

Задача*: в каком выпуклом многоугольнике диагоналей на 25 больше чем сторон?

25+n = nn-32

50 + 2n = n 2 - 3n

n 2 - 5n - 50 = 0

Разложим на множители

n 2 -25-5n -25 = 0

n=-5 не удовлетворяет,

так как не существует

такой многоугольник

n = 10 удовлетворяет

Ответ: Десяти угольник.

Фигуры с равными диагоналями.*

На плоскости существует два правильных многоугольника, у которых все диагонали равны между собой - это квадрат и правильный пятиугольник (пентагон) . У квадрата две одинаковых диагонали, пересекающихся в центре под прямым углом. У правильного пятиугольника пять одинаковых диагоналей, которые вместе образуют рисунок пятиконечной звезды (пентаграммы).

В пространстве существует единственный правильный многогранник (не многоугольник ), у которого все диагонали равны между собой - это правильный восьмигранник (октаэдр) . У октаэдра три диагонали, которые попарно перпендикулярно пересекаются в центре. Все диагонали октаэдра - пространственные (диагоналей граней у октаэдра нет, т.к. у него треугольные грани).

Помимо октаэдра есть еще один правильный многогранник, у которого все пространственные диагонали равны между собой - это куб (гексаэдр), помимо пространственных у куба есть диагонали граней . У куба четыре одинаковых пространственных диагонали, которые пересекаются в центре. Угол между диагоналями куба составляет либо arccos (1/3) ≈ 70,5° (для пары диагоналей, проведенных к смежным вершинам), либо arccos (–1/3) ≈ 109,5° (для пары диагоналей, проведенных к несмежным вершинам).

Четырехугольники.
Каждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали.

Две несмежные стороны называются противоположными.

Две не соседние вершины называются противоположными.
1.Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма:
1) Противоположные стороны параллелограмма равны. AB=DC, AD=BC.

2) Противоположные углы параллелограмма равны. A=C, B=D.

3) Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. AO=OC, BO=OD.

4) Сумма углов, прилежащих к одной стороне, равна 180°. A+D=180, A+B=180, B+C=180, D+C=180.

5) Сумма всех углов равна 360°. A+B+C+D=360°.

6)* Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: AC 2 +BD 2 =2∙(AB 2 +AD 2).

Задача 1*: Найти диагональ параллелограмма, если известно, что длина одной диагонали равна AC=9 см, а стороны AD=7 см и AB=4 см.

Решение: Подставив значения в формулу получим:

81+BD 2 =2∙(49+16),

BD 2 =49, следовательно вторая диагональ равна BD=7 см. Ответ: 7 см.
Задача 2*: Найти диагональ параллелограмма, если известно, что длина одной диагонали равна BD=10 см, а стороны AD=8 см и AB=2 см.

Решение: Условия задачи не верно, так как сумма двух сторон треугольника всегда больше третей стороны. Ответ: задача не имеет решений (смысла).

Задача 3*: а)Найти сторону параллелограмма, если известно, что длина диагоналей равна BD=6 см, AC=8, а одна сторона AB=5 см. б)Как называется этот параллелограмм.
Задача 4**: Сумма длин диагоналей параллелограмма равна 12 см, а произведение 32 найдите значение суммы квадратов всех его сторон.
Задача 5**: Найдите наибольший периметр параллелограмма, диагонали которого 6 см и 8 см.

Решение: Докажем, что среди всех параллелограммов с данными длинами диагоналей наибольший периметр имеет ромб .

Действительно, пусть a и b – длины соседних сторон параллелограмма, а и – длины его диагоналей (см. рис. 2). Тогда периметр параллелограмма: P = 2(a + b ).

Из равенства, выражающего теорему о сумме квадратов диагоналей параллелограмма, следует, что у всех параллелограммов с данными диагоналями сумма квадратов сторон есть величина постоянная.

По неравенству между средним арифметическим и средним квадратичным:  , причем равенство достигается т. и т. т., когда a = b . Значит, параллелограмм с наибольшим периметром является ромбом. Находим сторону этого ромба: =5(см). Ответ: 20 см.

2.Прямоугольник - это параллелограмм, у которого все углы прямые.
Определение 2: это четырёхугольник, у которого все углы прямые.

Определение 3: это параллелограмм, у которого один угол прямой.

Определение 4: это параллелограмм, у которого углы равны.
Свойства прямоугольника: +
1) Диагонали прямоугольника равны.

2)* Квадрат диагонали равен сумме квадратов сторон. AC 2 =AB 2 +DC 2

Задача 1: Меньшая сторона прямоугольника равна 5см, диагонали пересекаются под углом 60°. Найдите диагонали прямоугольника.
Задача 2: Меньшая сторона прямоугольника равна 24, диагонали пересекаются под углом 120°. Найдите диагонали и большую сторону прямоугольника.
Задача 3*: Сторона прямоугольника равна 3 см, диагональ 5 см. Найдите другую сторону прямоугольника.
Задача 4*: Сторона прямоугольника равна 6 см, диагональ 10 см. Найдите площадь прямоугольника.

3.Ромб - это параллелограмм, у которого все стороны равны.
Определение 2: это четырёхугольник, у которого все стороны равны.
Свойства ромба: те же свойства, что и у параллелограмма +
1) Диагонали ромба взаимно перпендикулярны (AC ⊥ BD).

2) Диагонали ромба делят его углы пополам (то есть диагонали ромба являются биссектрисами его углов- ∠DCA = ∠BCA, ∠ABD = ∠CBD, ∠BAC = ∠DAC, ∠ADB = ∠CDB).

3)*Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма). AC 2 +BD 2 =4·AB 2
Задача 1: Диагонали ромба 6 и 8 см. Найти сторону ромба.
Задача 2: Сторона ромба 10 см, один из углов 60. Найти маленькую диагональ ромба.
4.Квадрат -это параллелограмм, у которого все углы равны 90 и все стороны равны.
Определение 2: это параллелограмм, у которого все углы и стороны равны между собой.

Определение 3: это четырёхугольник, у которого все углы и стороны равны между собой.

Определение 4: это ромб, у которого один угол прямой.

Определение 5: это ромб, у которого углы равны.

Определение 6: это прямоугольник, у которого все стороны равны.
Свойства квадрата: те же свойства, что и у параллелограмма +
1) Диагонали квадрата равны.

2) Диагонали квадрата взаимно перпендикулярны (AC ⊥ BD).

3) Диагонали квадрата делят его углы пополам (то есть диагонали квадрата являются биссектрисами его углов- ∠DCA = ∠BCA= ∠ABD = ∠CBD= ∠BAC = ∠DAC= ∠ADB = ∠CDB=45).

4)* Квадрат диагонали равен удвоенному квадрату стороны. AC 2 =2·AB 2

5.Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Параллельные стороны называются основаниями, а две другие боковыми.

Трапеция называется равнобедренной, если ее боковые стороны равны.

Трапеция называется прямоугольной, если один из его углов прямой.
Задача: Докажите, что трапеция не может одновременно быть и прямоугольной и равнобедренной.

Определение

Вершина угла

Вершина угла - это точка, окуда берут начало два луча.

Вершина угла - это точка, откуда берут начало два луча ; где сходятся два отрезка; где две прямые пересекаются; где любая комбинация лучей, отрезков и прямых, образующих две (прямолинейные) «стороны», которые сходятся в одной точке .

Вершина многоугольника многогранника

В многоугольнике вершина называется «выпуклой », если внутренний угол многоугольника меньше π радиан (180° - два прямых угла). В противном случае вершина называется «вогнутой».

Более обще, вершина многогранника является выпуклой, если пересечение многогранника с достаточно малой сферой , имеющей вершину в качестве центра, представляет собой выпуклую фигуру; в противном же случае вершина является вогнутой.

Вершины многогранника связаны с вершинами графа , поскольку многогранника является графом, вершины которого соответствуют вершинам многогранника , а следовательно, граф многогранника можно рассматривать как одномерный симплициальный комплекс , вершинами которого служат вершины графа. Однако, в теории графов вершины могут иметь менее двух инцидентных рёбер , что обычно не разрешается для вершин геометрических. Также имеется связь между геометрическими вершинами и вершинами кривой , точками экстремумов её кривизны - вершины многоугольника в некотором смысле являются точками бесконечной кривизны, и, если многоугольник приблизить гладкой кривой, точки экстремальной кривизны будут лежать вблизи вершин многоугольника . Однако, приближение многоугольника с помощью гладкой кривой даёт дополнительные вершины в точках минимальной кривизны.

Вершины плоских мозаик

«Уши»

«Рты»

Основная вершина x i {\displaystyle x_{i}} простого многоугольника P {\displaystyle P} называется «ртом», если диагональ [ x i − 1 , x i + 1 ] {\displaystyle } лежит вне P {\displaystyle P} .

Число вершин многогранника

Любая поверхность трёхмерного выпуклого многогранника имеет эйлерову характеристику :

V − E + F = 2 , {\displaystyle V-E+F=2,}

где V {\displaystyle V} - число вершин, E {\displaystyle E} - число рёбер, а F {\displaystyle F} - число граней. Это равенство известно как уравнение Эйлера . К примеру, куб имеет 12 рёбер и 6 граней, а потому - 8 вершин: 8 − 12 + 6 = 2 {\displaystyle 8-12+6=2} .

Вершины в компьютерной графике

В компьютерной графике объекты часто представляются как триангулированные многогранники , в которых вершинам объекта сопоставляются не только три пространственные координаты , но и другая необходимая для правильного построения изображения объекта графическая информация, такая как цвет, отражательная способность , текстура , нормали вершин . Эти свойства используются при построении изображения с помощью

В разделе на вопрос Объясните, какая фигура называется многоугольником. Что такое вершины, стороны, диагонали и периметр многоугольника? заданный автором Арек Григорян лучший ответ это Многоугольник - это геометрическая фигура, определяется как замкнутая ломаная.
Вершины ломаной называются вершинами многоугольника, а отрезки - сторонами многоугольника.
Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.
Периметр многоугольника - это сумма длин всех многоугольника.
Источник: Спасибо Яндексу за это

Ответ от Ёоколёнок [гуру]

Ответ от Невролог [новичек]
Ответ ОТРЕЗОК!!!

Ответ от Особь [новичек]
огромное спасибо

Ответ от Простыня [новичек]
многоугольник - фигура имеющая больше 4х углов.
вершина - вершина угла, точка пересечения двух сторон.
сторона - ну собственно - сторона))) такая палочка, из которых он составлен
диагональ - линия проведенная из одного угла в другой
периметр - сумма длин всех сторон

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.