Продолжаем разбираться с системами линейных уравнений. До сих пор мы рассматривали системы, которые имеют единственное решение. Такие системы можно решить любым способом: методом подстановки («школьным»), по формулам Крамера, матричным методом , методом Гаусса . Однако на практике широко распространены еще два случая, когда:
1) система несовместна (не имеет решений);
2) система имеет бесконечно много решений.
Для этих систем применяют наиболее универсальный из всех способов решения – метод Гаусса . На самом деле, к ответу приведет и «школьный» способ, но в высшей математике принято использовать гауссовский метод последовательного исключения неизвестных. Те, кто не знаком с алгоритмом метода Гаусса, пожалуйста, сначала изучите урок метод Гаусса
Сами элементарные преобразования матрицы – точно такие же , разница будет в концовке решения. Сначала рассмотрим пару примеров, когда система не имеет решений (несовместна).
Пример 1
Что сразу бросается в глаза в этой системе? Количество уравнений – меньше, чем количество переменных. Есть такая теорема, которая утверждает:«Если количество уравнений в системе меньше количества переменных , то система либо несовместна, либо имеет бесконечно много решений». И это осталось только выяснить.
Начало решения совершенно обычное – запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1). На левой верхней ступеньке нам нужно получить (+1) или (–1). Таких чисел в первом столбце нет, поэтому перестановка строк ничего не даст. Единицу придется организовать самостоятельно, и сделать это можно несколькими способами. Мы поступили так. К первой строке прибавляем третью строку, умноженную на (–1).
(2). Теперь получаем два нуля в первом столбце. Ко второй строке прибавляем первую строку, умноженную на 3. К третьей строке прибавляем первую, умноженную на 5.
(3). После выполненного преобразования всегда целесообразно посмотреть, а нельзя ли упростить полученные строки? Можно. Вторую строку делим на 2, заодно получая нужную (–1) на второй ступеньке. Третью строку делим на (–3).
(4). К третьей строке прибавляем вторую строку. Наверное, все обратили внимание на нехорошую строку, которая получилась в результате элементарных преобразований:
![]() . Ясно, что так быть не может.
. Ясно, что так быть не может.
Действительно, перепишем полученную матрицу

обратно в систему линейных уравнений:

Если в результате элементарных преобразований получена строка вида, где λ – число, отличное от нуля, то система несовместна (не имеет решений).
Как записать концовку задания? Необходимо записать фразу:
«В результате элементарных преобразований получена строка вида , где λ ≠ 0 ». Ответ: «Система не имеет решений (несовместна)».
Обратите внимание, что в этом случае нет никакого обратного хода алгоритма Гаусса, решений нет и находить попросту нечего.
Пример 2
Решить систему линейных уравнений 
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Снова напоминаем, что Ваш ход решения может отличаться от нашего хода решения, метод Гаусса не задаёт однозначного алгоритма, о порядке действий и о самих действиях надо догадываться в каждом случае самостоятельно.
Еще одна техническая особенность решения: элементарные преобразования можно прекращать сразу же , как только появилась строка вида , где λ ≠ 0 . Рассмотрим условный пример: предположим, что после первого же преобразования получилась матрица
 .
.
Эта матрица еще не приведена к ступенчатому виду, но в дальнейших элементарных преобразованиях нет необходимости, так как появилась строка вида , где λ ≠ 0 . Следует сразу дать ответ, что система несовместна.
Когда система линейных уравнений не имеет решений – это почти подарок студенту, ввиду того, что получается короткое решение, иногда буквально в 2-3 действия. Но всё в этом мире уравновешено, и задача, в которой система имеет бесконечно много решений – как раз длиннее.
Пример 3:
Решить систему линейных уравнений

Тут 4 уравнений и 4 неизвестных, таким образом, система может иметь либо единственное решение, либо не иметь решений, либо иметь бесконечно много решений. Как бы там ни было, но метод Гаусса в любом случае приведет нас к ответу. В этом и его универсальность.
Начало опять стандартное. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Вот и всё, а вы боялись.
(1). Обратите внимание, что все числа в первом столбце делятся на 2, поэтому на левой верхней ступеньке нас устраивает и двойка. Ко второй строке прибавляем первую строку, умноженную на (–4). К третьей строке прибавляем первую строку, умноженную на (–2). К четвертой строке прибавляем первую строку, умноженную на (–1).
Внимание! У многих может возникнуть соблазн из четвертой строки вычесть первую строку. Так делать можно, но не нужно, опыт показывает, что вероятность ошибки в вычислениях увеличивается в несколько раз. Только складываем: к четвертой строке прибавляем первую строку, умноженную на (–1) – именно так!
(2). Последние три строки пропорциональны, две из них можно удалить. Здесь опять нужно проявить повышенное внимание , а действительно ли строки пропорциональны? Для перестраховки не лишним будет вторую строку умножить на (–1), а четвертую строку разделить на 2, получив в результате три одинаковые строки. И только после этого удалить две из них. В результате элементарных преобразований расширенная матрица системы приведена к ступенчатому виду:

При оформлении задачи в тетради желательно для наглядности делать такие же пометки карандашом.
Перепишем соответствующую систему уравнений: 
«Обычным» единственным решением системы здесь и не пахнет. Нехорошей строки , где λ ≠ 0, тоже нет. Значит, это и есть третий оставшийся случай – система имеет бесконечно много решений.
Бесконечное множество решений системы коротко записывают в виде так называемого общего решения системы .
Общее решение системы найдем с помощью обратного хода метода Гаусса. Для систем уравнений с бесконечным множеством решений появляются новые понятия: «базисные переменные» и «свободные переменные» . Сначала определим, какие переменные у нас являются базисными , а какие переменные - свободными . Не обязательно подробно разъяснять термины линейной алгебры, достаточно запомнить, что вот существуют такие базисные переменные и свободные переменные .
Базисные переменные всегда «сидят» строго на ступеньках матрицы . В данном примере базисными переменными являются x 1 и x 3 .
Свободные переменные – это все оставшиеся переменные, которым не досталось ступеньки. В нашем случае их две: x 2 и x 4 – свободные переменные.
Теперь нужно все базисные переменные выразить только через свободные переменные . Обратный ход алгоритма Гаусса традиционно работает снизу вверх. Из второго уравнения системы выражаем базисную переменную x 3:
Теперь смотрим на первое уравнение: ![]() . Сначала в него подставляем найденное выражение :
. Сначала в него подставляем найденное выражение :
![]()
Осталось выразить базисную переменную x 1 через свободные переменные x 2 и x 4:

В итоге получилось то, что нужно – все базисные переменные (x 1 и x 3) выражены только через свободные переменные (x 2 и x 4):
![]()
Собственно, общее решение готово:
![]() .
.
Как правильно записать общее решение? Прежде всего, свободные переменные записываются в общее решение «сами по себе» и строго на своих местах. В данном случае свободные переменные x 2 и x 4 следует записать на второй и четвертой позиции:
 .
.
Полученные же выражения для базисных переменных ![]() и , очевидно, нужно записать на первой и третьей позиции:
и , очевидно, нужно записать на первой и третьей позиции:

Из общего решения системы можно найти бесконечно много частных решений . Это очень просто. Свободными переменные x 2 и x 4 называют так, потому что им можно придавать любые конечные значения . Самыми популярными значениями являются нулевые значения, поскольку при этом частное решение получается проще всего.
Подставив (x 2 = 0; x 4 = 0) в общее решение, получим одно из частных решений:
![]() , или – это частное решение, соответствующее свободным переменным при значениях (x
2 = 0; x
4 = 0).
, или – это частное решение, соответствующее свободным переменным при значениях (x
2 = 0; x
4 = 0).
Другой сладкой парочкой являются единицы, подставим (x 2 = 1 и x 4 = 1) в общее решение:
![]() , т. е. (-1; 1; 1; 1) – еще одно частное решение.
, т. е. (-1; 1; 1; 1) – еще одно частное решение.
Легко заметить, что система уравнений имеет бесконечно много решений, так как свободным переменным мы можем придать любые значения.
Каждое частное решение должно удовлетворять каждому уравнению системы. На этом основана «быстрая» проверка правильности решения. Возьмите, например, частное решение (-1; 1; 1; 1) и подставьте его в левую часть каждого уравнения исходной системы:

Всё должно сойтись. И с любым полученным вами частным решением – тоже всё должно сойтись.
Строго говоря, проверка частного решения иногда обманывает, т.е. какое-нибудь частное решение может удовлетворять каждому уравнению системы, а само общее решение на самом деле найдено неверно. Поэтому, прежде всего, более основательна и надёжна проверка общего решения.
Как проверить полученное общее решение ![]() ?
?
Это несложно, но довольно требует длительных преобразований. Нужно взять выражения базисных
переменных, в данном случае ![]() и , и подставить их в левую часть каждого уравнения системы.
и , и подставить их в левую часть каждого уравнения системы.
В левую часть первого уравнения системы:

Получена правая часть исходного первого уравнения системы.
В левую часть второго уравнения системы:

Получена правая часть исходного второго уравнения системы.
И далее – в левые части третьего и четвертого уравнение системы. Эта проверка дольше, но зато гарантирует стопроцентную правильность общего решения. Кроме того, в некоторых заданиях требуют именно проверку общего решения.
Пример 4:
Решить систему методом Гаусса. Найти общее решение и два частных. Сделать проверку общего решения.

Это пример для самостоятельного решения. Здесь, кстати, снова количество уравнений меньше, чем количество неизвестных, а значит, сразу понятно, что система будет либо несовместной, либо с бесконечным множеством решений.
Пример 5:
Решить систему линейных уравнений. Если система имеет бесконечно много решений, найти два частных решения и сделать проверку общего решения

Решение: Запишем расширенную матрицу системы и, с помощью элементарных преобразований, приведем ее к ступенчатому виду:

(1). Ко второй строке прибавляем первую строку. К третьей строке прибавляем первую строку, умноженную на 2. К четвертой строке прибавляем первую строку, умноженную на 3.
(2). К третьей строке прибавляем вторую строку, умноженную на (–5). К четвертой строке прибавляем вторую строку, умноженную на (–7).
(3). Третья и четвертая строки одинаковы, одну из них удаляем. Вот такая красота:

Базисные переменные сидят на ступеньках, поэтому – базисные переменные.
Свободная переменная, которой не досталось ступеньки здесь всего одна: .
(4). Обратный ход. Выразим базисные переменные через свободную переменную:
Из третьего уравнения:
![]()
Рассмотрим второе уравнение и подставим в него найденное выражение :
![]() ,
, ![]() , ,
, ,
Рассмотрим первое уравнение и подставим в него найденные выражения и :

Таким образом, общее решение при одной свободной переменной x 4:
![]()
Еще раз, как оно получилось? Свободная переменная x 4 одиноко сидит на своём законном четвертом месте. Полученные выражения для базисных переменных , , - тоже на своих местах.
Сразу выполним проверку общего решения.
Подставляем базисные переменные , , в левую часть каждого уравнения системы:




Получены соответствующие правые части уравнений, таким образом, найдено верное общее решение.
Теперь из найденного общего решения ![]() получим два частных решения. Все переменные выражаются здесь через единственную свободную переменную x
4 . Ломать голову не нужно.
получим два частных решения. Все переменные выражаются здесь через единственную свободную переменную x
4 . Ломать голову не нужно.
Пусть x
4 = 0, тогда ![]() – первое частное решение.
– первое частное решение.
Пусть x
4 = 1, тогда ![]() – еще одно частное решение.
– еще одно частное решение.
Ответ:
Общее решение: ![]() . Частные решения:
. Частные решения:
![]() и .
и .
Пример 6:
Найти общее решение системы линейных уравнений.

Проверка общего решения у нас уже сделана, ответу можно доверять. Ваш ход решения может отличаться от нашего хода решения. Главное, чтобы совпали общие решения. Наверное, многие заметили неприятный момент в решениях: очень часто при обратном ходе метода Гаусса нам пришлось возиться с обыкновенными дробями. На практике это действительно так, случаи, когда дробей нет – встречаются значительно реже. Будьте готовы морально, и, самое главное, технически.
Остановимся на особенностях решения, которые не встретились в прорешанных примерах. В общее решение системы иногда может входить константа (или константы).
Например, общее решение: . Здесь одна из базисных переменных равна постоянному числу: . В этом нет ничего экзотического, так бывает. Очевидно, что в данном случае любое частное решение будет содержать пятерку на первой позиции.
Редко, но встречаются системы, в которых количество уравнений больше количества переменных . Однако метод Гаусса работает в самых суровых условиях. Следует невозмутимо привести расширенную матрицу системы к ступенчатому виду по стандартному алгоритму. Такая система может быть несовместной, может иметь бесконечно много решений, и, как ни странно, может иметь единственное решение.
Повторимся в своем совете – чтобы комфортно себя чувствовать при решении системы методом Гаусса, следует набить руку и прорешать хотя бы десяток систем.
Решения и ответы:
Пример 2:
Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
Выполненные элементарные преобразования:
(1) Первую и третью строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на (–6). К третьей строке прибавили первую строку, умноженную на (–7).
(3) К третьей строке прибавили вторую строку, умноженную на (–1).
В результате элементарных преобразований получена строка вида , где λ ≠ 0 . Значит, система несовместна. Ответ: решений нет.
Пример 4:
Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования:
(1). Ко второй строке прибавили первую строку, умноженную на 2. К третьей строке прибавили первую строку, умноженную на 3.
Для второй ступеньки нет единицы , и преобразование (2) направлено на её получение.
(2). К третьей строке прибавили вторую строку, умноженную на –3.
(3). Вторую с третью строки поменяли местами (переставили полученную –1 на вторую ступеньку)
(4). К третьей строке прибавили вторую строку, умноженную на 3.
(5). У первых двух строк сменили знак (умножили на –1), третью строку разделили на 14.
Обратный ход:
(1). Здесь – базисные переменные (которые на ступеньках), а – свободные переменные (кому не досталось ступеньки).
(2). Выразим базисные переменные через свободные переменные:
Из третьего уравнения: .
(3). Рассмотрим второе уравнение: , частные решения:
Ответ:
Общее решение:
![]()
Комплексные числа
В этом разделе мы познакомимся с понятием комплексного числа , рассмотрим алгебраическую , тригонометрическую и показательную форму комплексного числа. А также научимся выполнять действия с комплексными числами: сложение, вычитание, умножение, деление, возведение в степень и извлечение корня.
Для освоения комплексных чисел не требуется каких-то специальных знаний из курса высшей математики, и материал доступен даже школьнику. Достаточно уметь выполнять алгебраические действия с «обычными» числа, и помнить тригонометрию.
Сначала вспомним «обычные» Числа. В математике они называются множеством действительных чисел и обозначаются буквой R, либо R (утолщённой). Все действительные числа сидят на знакомой числовой прямой:

Компания действительных чисел очень пёстрая – здесь и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой оси обязательно соответствует некоторое действительное число.
Отыскание решений линейной системыПортабельные Windows-приложения на сайте Bodrenko.com
§2. Отыскание решений линейной системы
Теорема Кронекера-Капелли устанавливает необходимое и
достаточное условие совместности линейной системы, но не дает способа нахождения
решений этой системы.
В этом параграфе мы займемся отысканием решений линейной системы (3.1). Сначала
мы рассмотрим простейший случай квадратной системы линейных уравнений с отличным
от нуля определителем основной матрицы, а затем перейдем к отысканию
совокупности всех решений общей линейной системы вида (3.1).
1. Квадратная система линейных уравнений с определителем основной
матрицы, отличным от нуля.
Пусть дана квадратная система линейных
уравнений
с отличным от нуля определителем Δ основной матрицы

Докажем, что такая система имеет, и притом единственное,
решение, и найдем это решение. Сначала докажем, что система (3.10) может иметь
только одно решение (т. е. докажем единственность решения системы (3.10) в
предположении его существования).
Предположим, что существуют какие-либо n чисел х 1 , x 2 ,...,х n
такие, что при подстановке этих чисел в систему (3.10) все уравнения этой
системы обращаются в тождества (т. е. существует некоторое решение системы
(3.10) х 1 , x 2 ,...,х n). Тогда, умножая тождества
(3.10) соответственно на алгебраические дополнения A 1j , A 2j ,...,
A nj элементов j-ro столбца определителя Δ
матрицы (3.11) и складывая затем получающиеся при этом тождества, мы получим
(для любого номера j, равного 1, 2,..., n)
Учитывая, что сумма произведений элементов i-го столбца на
соответствующие алгебраические дополнения элементов j-ro столбца равна нулю при
i ≠
j и равна определителю Δ
матрицы (3.11) при i = j (cм. свойство 4° из п. 4 §2 гл. 1), мы получим из
последнего равенства
x j Δ = b 1 A 1j + b 2 A 2j + ... + b n A nj . (3.12)
Обозначим символом
Δ
j
(b
i
)
(или, более кратко, символом
Δ
j
)
определитель, получающийся из определителя
Δ
основной матрицы (3.11) заменой его j-го столбца столбцом из свободных членов b
1
,
b
2
,...,b
n
(с
сохранением без изменения всех остальных столбцов
Δ
).
Заметим, что в правой части (3.12) стоит именно определитель
Δ
j (b i) (ч
тобы
убедиться в этом, достаточно записать разложение определителя
Δ
j (b i) по элементам i-го
столбца
), и это равенство принимает вид
Δ x j = Δ j (3.13)
Поскольку определитель Δ
матрицы
(3.11) отличен от нуля, равенства (3.13) эквивалентны соотношениям
Итак, мы доказали, что если решение х
1
, x
2
,...,х
n
системы (3.10) с определителем
Δ
основной матрицы (3.11), отличным от нуля, существует, то это решение однозначно
определяется формулами (3.14)
.
Формулы (3.14) называются формулами Крамера
.
Еще раз подчеркнем, что формулы Крамера пока получены нами в предположении
существования решения и доказывают его единственность.
Остается доказать существование решения системы (3.10). Для э
того
в силу теоремы Кронекера-Капелли достаточно доказать, что ранг основной матрицы
(3.11) равен рангу расширенной матрицы (cуществует и другой способ
доказательства существования решения системы (3.10), заключающийся в проверке
того, что числа х 1 , x 2 ,...,х n , определяемые
формулами Крамера (3.14), обращают в тождества все уравнения системы (3.10))

но это очевидно, ибо в силу соотношения Δ
≠
0, ранг основной матрицы равен n, а ранг содержащей n строк расширенной
матрицы (3.15) больше числа n быть не может и потому равен рангу основной
матрицы.
Тем самым полностью доказано, что квадратная система линейных уравнений
(3.10) с определителем основной матрицы, отличным от нуля, имеет, и притом
единственное, решение, определяемое формулами Крамера (3.14).
Доказанное нами утверждение еще проще устанавливается матричным способом. Для того чтобы сделать это, заменим (как и в п. 1 § 1) систему (3.10) эквивалентным ей матричным уравнением
AX = B,
(3.16)
где А - основная матрица системы (3.11), а X и В - столбцы,

первый из которых подлежит определению, а второй задан.
Так как определитель Δ
матрицы А отличен от нуля, то
существует обратная матрица А -1 (см. п. 7 §2 гл. 1).
Предположим, что существует решение системы (3.10), т.е. существует столбец X,
обращающий в тождество матричное уравнение (3.16). Помножая указанное тождество
слева на обратную матрицу А -1 будем иметь
А -1 (АХ) =А -1 В. (3.17)
Учтем теперь, что в силу сочетательного свойства произведения трех матриц (см. п. 2 § 1 гл. 1) и в силу соотношения А -1 А = Е, где Е - единичная матрица (см. п. 7 §2 гл. 1), А -1 (АХ) = (А -1 А)Х = ЕХ = X, так что мы получим из (3.17)
X = А -1 В. (3.18)
Развертывая равенство (3.18) и учитывая вид обратной матрицы
(cм. формулу A.41) из п. 7 §2 гл. 1), мы и получим для элементов столбца X
формулы Крамера.
Итак, мы доказали, что если решение матричного уравнения (3.16) существует, то
оно однозначно определяется соотношением (3.18), эквивалентным формулам Крамера.
Легко проверить, что столбец X, определяемый соотношением (3.18), в самом деле
является решением матричного уравнения (3.16),
т. е. при подстановке в это уравнение обращает его в тождество. В самом деле,
если столбец X определяется равенством (3.18), то АХ = А(А -1 В) = (АА -1)В
= ЕВ = В.
Итак, если определитель Δ
матрицы А отличен от нуля
(т. е. если эта матрица является невырожденной), то существует, и притом
единственное, решение матричного уравнения (3.16), определяемое соотношением
(3.18), эквивалентным формулам Крамера.
Пример. Найдем решение квадратной системы линейных уравнений

с отличным от нуля определителем основной матрицы

Поскольку

то, в силу формул Крамера, единственное решение
рассматриваемой системы имеет вид х 1 = 1, х 2 = 2, x 3
= 3, х 4 = 4.
Основное значение формул Крамера состоит в том, что они дают явное выражение для
решения квадратной системы линейных уравнений (с определителем, отличным от
нуля) через коэффициенты уравнений и свободные члены. Практическое использование
формул Крамера связано с довольно громоздкими вычислениями (для решения системы
n уравнений с n неизвестными приходится вычислять (n + 1) определитель n-го
порядка). К этому следует добавить, что если коэффициенты уравнений и свободные
члены представляют собой лишь приближенные значения каких - либо измеряемых
физических величин или округляются в процессе вычислений, то использование
формул Крамера может привести к большим ошибкам и в ряде случаев является
нецелесообразным.
В §4 гл.4 будет изложен метод регуляризации, принадлежащий А.Н. Тихонову и
позволяющий находить решение линейной системы с точностью, соответствующей
точности задания матрицы коэффициентов уравнений и столбца свободных членов, а в
гл. 6 дается представление о так называемых итерационных методах решения
линейных систем, позволяющих решать эти системы при помощи последовательных
приближений неизвестных.
В заключении отметим, что в этом пункте мы исключили из рассмотрения случай
обращения в нуль определителя Δ
основной матрицы
системы (3.10). Этот случай будет содержаться в общей теории систем m линейных
уравнений с n неизвестными, излагаемой в следующем пункте.
2. Отыскание всех решений общей линейной системы.
Рассмотрим
теперь общую систему m линейных уравнений с n неизвестными (3.1). Предположим,
что эта система совместна и что ранг ее основной и расширенной матриц равен
числу r. Не ограничивая общности, мы можем предположить, что базисный минор
основной матрицы (3.2) находится в левом верхнем углу этой матрицы (общий случай
сводится к этому случаю посредством перестановки в системе (3.1) уравнений и
неизвестных).
Тогда первые r строк как основной матрицы (3.2), так и расширенной матрицы (3.8)
являются базисными строками этих матриц (т
ак как ранги
основной и расширенной матриц оба равны r, то базисный минор основной матрицы
будет одновременно являться базисным минором и расширенной матрицы), и, по
теореме 1.6 о базисном миноре, каждая из строк расширенной матрицы (1.8),
начиная с (r + 1)-й строки, является линейной комбинацией п
ервых
r строк этой матрицы.
В терминах системы (3.1) это означает, что каждое из уравнений этой системы,
начиная с (r + 1)-го уравнения, является линейной комбинацией (т. е. следствием)
первых r уравнений этой системы (т. е. всякое решение первых г уравнений
системы (3.1) обращает в тождества и все последующие уравнения этой системы
).
Таким образом, достаточно найти все решения лишь первых r уравнений системы
(3.1). Рассмотрим первые r уравнений системы (3.1), записав их в виде
Если мы придадим неизвестным х r+1 ,...,х n
совершенно произвольные значения c r+1 ,...,c n , то система
(1.19) превратится в квадратную систему r линейных уравнений для r неизвестных х 1 , x 2 ,...,х r
, причем определителем основной матрицы этой системы является отличный от
нуля базисный минор матрицы (3.2). В силу результатов предыдущего пункта, эта
система (3.19) имеет единственное решение, определяемое формулами Крамера, т. е.
для произвольно выбранных c r+1 ,...,c n существует
единственная совокупность r чисел c 1 ,...,c r , обращающих в
тождества все уравнения системы (3.19) и определяющихся формулами Крамера.
Чтобы записать это единственное решение, договоримся обозначать символом M j (d i)
определитель, получающийся из базисного минора М матрицы (3.2) заменой его j-ro
столбца столбцом из чисел d 1 , d 2 ,...,d i ,...,d r
(с сохранением без изменения всех остальных столбцов М). Тогда, записывая
решение системы (3.19) с помощью формул Крамера и пользуясь линейным свойством
определителя, мы получим

Формулы (3.20) выражают значения неизвестных x j = c j
(j = 1, 2,......, r) через коэффициенты при неизвестных, свободные члены и
произвольно заданные параметры с r+1 ,...., с n .
Докажем, что формулы (3.20) содержат любое решение системы (3.1)
. В
самом деле, пусть c (0) 1 , c (0) 2 ,...,c (0) r ,
c (0) r+1 , ...,c (0) n - произвольное
решение указанной системы. Тогда оно является решением и системы (3.19). Но из
системы (3.19) величины
c (0) 1 , c (0) 2 ,...,c (0) r ,
определяются через величины c (0) r+1 , ...,c (0) n
однозначно и именно по формулам Крамера (3.20). Таким образом, при с
r+1
= c
(0)
r+1 ,
...,
с
n
= c
(0)
n
формулы (3.20) дают нам как раз рассматриваемое решение c
(0)
1
,
c
(0)
2
,...,c
(0)
r
,
c
(0)
r+1 ,
...,c
(0)
n
.
Замечание.
Если ранг r основной и расширенной матриц системы
(3.1) равен числу неизвестных n, то в этом случае соотношения (3.20) переходят в
формулы
![]()
определяющие единственное решение системы (3.1). Таким
образом, система (3.1) имеет единственное решение (т.е. является определенной)
при условии, что ранг r основной и расширенной ее матриц равен числу неизвестных
n (и меньше числа уравнений m или равен ему).
Пример. Найдем все решения линейной системы

Нетрудно убедиться в том, что ранг как основной, так и
расширенной матрицы этой системы равен двум (т. е. эта система совместна),
причем можно считать, что базисный минор М стоит в левом верхнем углу основной
матрицы, т. е. ![]() . Но тогда, отбрасывая два последних
уравнения и задавая произвольно с 3 и с 4 , мы получим
систему
. Но тогда, отбрасывая два последних
уравнения и задавая произвольно с 3 и с 4 , мы получим
систему
x 1 - x 2 = 4 - c 3 + c 4 ,
x 1 + x 2 = 8 - 2c 3 - 3c 4 ,
из которой в силу формул Крамера получаем значения
x 1 = c 1 = 6 - 3/2 c 3 - c 4 , x 2 = c 2 = 2 - 1/2 c 3 - 2c 4 . (3.22)
Таким образом, четыре числа
(6 - 3/2 c 3 - c 4 ,2 - 1/2 c 3 - 2c 4 ,c 3 , c 4) (3.23)
при произвольно заданных значениях с 3 и с 4
образуют решение системы (3.21), причем строка (3.23) содержит все решения этой
системы.
3. Свойства совокупности решений однородной системы.
Рассмотрим теперь однородную систему m линейных уравнений с n
неизвестными (3.7), предполагая, как и выше, что матрица (3.2) имеет ранг,
равный r, и что базисный минор М расположен в левом верхнем углу этой матрицы.
Поскольку на этот раз все b i равны нулю, вместо формул (3.20) мы
получим следующие формулы:
выражающие значения неизвестных x j = c j
(j = 1, 2,..., r) через коэффициенты при неизвестных и произвольно заданные
значения c r+1 ,...,c n . В силу доказанного в предыдущем
пункте формулы (3.24) содержат любое решение однородной системы (3.7)
.
Убедимся теперь в том, что совокупность всех решений однородной системы
(3.7) образует линейное пространство
.
Пусть Х 1 = (x (1) 1 , x (1) 2 ,...,x (1) n) и Х 2 = (x (2) 1 , x (2) 2 ,...,x (2) n) - два произвольных решения однородной системы (3.7), а λ
- любое вещественное число. В силу того, что каждое решение однородной системы
(3.7) является элементом линейного пространства А n всех упорядоченных
совокупностей n чисел, достаточно доказать, что каждая из двух совокупностей
Х 1 + Х 2 = (x (1) 1 + x (2) 1 ,..., x (1) n + x (2) n)
λ Х 1 = (λ x (1) 1 ,...,λ x (1) n)
также является решением однородной системы (3.7).
Рассмотрим любое уравнение системы (3.7), например i-е уравнение, и подставим в
это уравнение на место неизвестных элементы указанных совокупностей. Учитывая,
что Х 1 и Х 2 - решения однородной системы, будем иметь

а это и означает, что совокупности Х 1 + Х 2
и λ
Х 1 являются решениями однородной
системы (3.7).
Итак, совокупность всех решений однородной системы (3.7) образует линейное
пространство, которое мы обозначим символом R.
Найдем размерность этого пространства R и построим в нем базис.
Докажем, что в предположении о том, что ранг матрицы однородной системы (3.7)
равен r, линейное пространство R всех решений однородной системы (3.7)
изоморфно линейному пространству А
n-r
всех
упорядоченных совокупностей (n - r) чисел
(п
ространство
А m введено в примере 3 п. 1 § 1 гл. 2).
Поставим в соответствие каждому решению (c 1 ,...,c r ,
c r+1 ,...,c n) однородной системы (3.7) элемент (c r+1 ,...,c n)
пространства А
n-r
Поскольку числа c r+1 ,...,c n
могут быть выбраны произвольно и при каждом выборе с помощью формул (3.24)
однозначно определяют решение системы (3.7), то установленное нами соответствие
является взаимно однозначным
. Далее заметим, что если элементы c (1) r+1 ,...,c (1) n
и c (2) r+1 ,...,c (2) n пространства
А
n-r
отвечают элементам
(c (1) 1 ,...,c (1) r ,
c (1) r+1 ,...,c (1) n)и (c (2) 1 ,...,c (2) r , c (2) r+1 ,...,c (2) n)
пространства R, то из формул (3.24) сразу же следует, что элементу (c (1) r+1
+ c (2) r+1 ,...,c (1) n +c (2) n)
отвечает элемент
(c (1) 1 + c (2) 1 ,...,c (1) r
+ c (2) r , c (1) r+1 +
c (2) r+1 ,...,c (1) n +c (2) n),
а элементу (λ
c (1) r+1 ,...,λ
c (1) n) при любом вещественном λ
отвечает элемент
(λ
c (1) 1 ,...,λ
c (1) r ,
λ
c (1) r+1 ,...,λ
c (1) n).
Тем самым доказано, что установленное нами соответствие является изоморфизмом.
Итак, линейное пространство R всех решений однородной системы (3.7) с n
неизвестными и рангом основной матрицы, равным r, изоморфно пространству А
n-r
и, стало быть, имеет размерность n - r.
Любая совокупность из (n - r) линейно независимых решений однородной системы
(3.7) образует (в силу теоремы 2.5) базис в пространстве R всех решений и
называется фундаментальной совокупностью решений однородной системы (3.7).
Для построения фундаментальной совокупности решений можно отправляться от любого
базиса пространства А
n-r
. Отвечающая этому базису
совокупность решений системы (3.7), в силу изоморфизма, будет линейно
независимой и поэтому будет являться фундаментальной совокупностью решений.
Особо выделяют фундаментальную совокупность решений системы (3.7), отвечающую
простейшему базису e 1 = (1, 0, 0,..., 0),
е 2 = (1, 1, 0,..., 0), ..., е n-r = (0, 0, 0,..., 1)
пространства А
n-r
и называемую нормальной
фундаментальной совокупностью решений однородной системы (3.7).
При сделанных выше предположениях о ранге и расположении базисного минора, в
силу формул (3.24), нормальная фундаментальная совокупность решений однородной
системы (3.7) имеет вид:

По определению базиса любое решение X однородной системы (3.7)
представимо в виде
X= C 1 X 1 + C 2 X 2 + ... + C n-r X n-r , (3.26)
где C 1 , C 2 , ...,C n-r -
некоторые постоянные. Поскольку в формуле (3.26) содержится любое решение
однородной системы (3.7), то эта формула дает общее решение рассматриваемой
однородной системы.
Пример. Рассмотрим однородную систему уравнений:

соответствующую неоднородной системе (3.21), разобранной в
примере в конце предыдущего пункта. Там мы выяснили, что ранг r матрицы этой
системы равен двум, и взяли в качестве базисного минор, стоящий в левом верхнем
углу указанной матрицы.
Повторяя рассуждения, проведенные в конце предыдущего пункта, мы получим вместо
формул (3.22) соотношения
c 1 = - 3/2 c 3 - c 4 , c 2 = - 1/2 c 3 - 2c 4 ,
справедливые при произвольно выбранных c 3 и c 4 .
С помощью этих соотношений (полагая сначала c 3 =1,c 4 =0, а
затем c 3 = 0,c 4 = 1) мы получим нормальную фундаментальную
совокупность двух решений системы (3.27):
X 1 = (-3/2,-1/2,1,0), X 2 = (-1,-2,
0,1).
(3.28)
где С 1 и С 2 - произвольные постоянные.
В заключение этого пункта установим связь между решениями неоднородной линейной
системы (3.1) и соответствующей ей однородной системы (3.7) (c теми же самыми
коэффициентами при неизвестных). Докажем следующие два утверждения.
1°. Сумма любого решения неоднородной системы (3.1) с любым решением
соответствующей однородной системы (3.7) представляет собой решение системы
(3.1).
В самом деле, если c 1 ,...,c n - решение системы (3.1), a d 1 ,...,d n
- решение соответствующей ей однородной системы (3.7), то, подставив в любое
(например, в i-е) уравнение системы (3.1) на место неизвестных числа c 1
+ d 1 ,...,c n + d n , получим
что и требовалось доказать.
2°. Разность двух произвольных решений неоднородной системы (3.1) является
решением соответствующей однородной системы (3.7).
В самом деле, если c" 1 ,...,c" n и c" 1 ,...,c" n
- два произвольных решения системы (3.1), то, подставив в любое (например, в i-е)
уравнение системы (3.7) на место неизвестных числа c" 1 - c" 1 ,...,c" n
- c" n получим
что и требовалось доказать.
Из доказанных утверждений вытекает, что, найдя одно решение неоднородной
системы (3.1) и складывая его с каждым решением соответствующей однородной
системы (3.7), мы получим все решения неоднородной системы (3.1).
Другими словами, сумма частного решения неоднородной системы (3.1) и общего
решения соответствующей однородной системы (3.7) дает общее решение неоднородной
системы (3.1).
В качестве частного решения неоднородной системы (3.1) естественно взять то его
решение (п
ри этом предполагается, как и выше, что ранги
основной и расширенной матриц системы (3.1) равны r и что базисный минор
находится в левом верхнем углу этих матриц)
которое получится, если в формулах (3.20) положить равными
нулю все числа c r+1 ,...,c n . Складывая это частное решение
с общим решением (3.26) соответствующей однородной системы, мы получим следующее
выражение для общего решения неоднородной системы (3.1):
X= X 0 + C 1 X 1 + C 2 X 2 + ... + C n-r X n-r . (3.30)
В этом выражении X 0 обозначает частное решение
(3.29), C 1 , C 2 , ... , C n-r - произвольные
постоянные, а X 1 ,X 2 ,... ,X n-r - элементы
нормальной фундаментальной совокупности решений (3.25) соответствующей
однородной системы.
Так, для рассмотренной в конце предыдущего пункта неоднородной системы (3.21)
частное решение вида (3.29) равно Х 0 =(6,2,0, 0).
Складывая это частное решение с общим решением (3.28) соответствующей однородной
системы (3.27), мы получим следующее общее решение неоднородной системы (3.21):
X = (6,2,0, 0) + C 1 (-3/2,-1/2,1,0) + C 2 (-1,-2, 0,1). (3.31)
Здесь C 1 и C 2 - произвольные постоянные.
4. Заключительные замечания о решении линейных систем.
Развитые
в предыдущих пунктах методы решения линейных систем
упираются в необходимость вычисления ранга матрицы и нахождения ее базисного
минора. После того, как базисный минор найден, решение сводится к технике
вычисления определителей и к использованию формул Крамера.
Для вычисления ранга матрицы можно использовать следующее правило: при
вычислении ранга матрицы следует переходить от миноров меньших порядков к
минорам больших порядков; при этом, если уже найден отличный от нуля минор М
порядка k, то требуют вычисления лишь миноры порядка (k + 1), окаймляющие
(т
о
есть содержащие внутри себя минор М) этот минор М; в случае равенства нулю
всех окаймляющих миноров порядка (k + 1) ранг матрицы равен к
(в
самом деле, в указанном случае все строки (столбцы) матрицы принадлежат линейной
оболочке ее k строк (столбцов), на пересечении которых стоит минор М, а
размерность указанной линейной оболочки равна k).
Укажем и другое правило вычисления ранга матрицы. Заметим, что со строками
(столбцами) матрицы можно производить три элементарные операции
, не
изменяющие ранга этой матрицы: 1) перестановку двух строк (или двух столбцов),
2) умножение строки (или столбца) на любой отличный от нуля множитель, 3)
прибавление к одной строке (столбцу) произвольной линейной комбинации других
строк (столбцов) (э
ти три операции не изменяют ранга
матрицы вследствие того, что операции 1) и 2) не изменяют максимального числа
линейно независимых строк (столбцов) матрицы, а операция 3) обладает тем
свойством, что линейная оболочка всех строк (столбцов), имевшихся до проведения
этой операции, совпадает с линейной оболочкой всех строк (столбцов), полученных
после проведения этой операции).
Будем говорить, что матрица ||а ij ||, содержащая m строк и n столбцов,
имеет диагональный
вид, если равны нулю все ее элементы, отличные от а 11 ,
а 22 ,.., a rr , где r = min{m, n}. Ранг такой матрицы,
очевидно, равен r.
Убедимся в том, что посредством трех элементарных операций любую матрицу

можно привести к диагональному виду (что и позволяет вычислить ее ранг).
В самом деле, если все элементы матрицы (3.31) равны нулю, то
эта матрица уже приведена к диагональному виду. Если же у мат-
рицы (3.31) есть отличные от нуля элементы, то путем перестановки двух строк и
двух столбцов можно добиться того, чтобы был отличен от нуля элемент а 11 .
Умножая после этого первую строку матрицы на а 11 -1 , мы
превратим элемент а 11 в единицу. Вычитая далее из j-ro столбца
матрицы (при j = 2, 3,..., n) первый столбец, умноженный на а i1 , а
затем вычитая из i-й строки (при i = 2, 3,..., n) первую строку, умноженную на а i1 ,
мы получим вместо (3.31) матрицу следующего вида:

Совершая уже описанные нами операции с матрицей, взятой в
рамку, и продолжая действовать аналогичным способом, мы после конечного числа
шагов получим матрицу диагонального вида.
Изложенные в предыдущих пунктах методы решения линейных систем, использующие, в
конечном итоге, аппарат формул Крамера, могут привести к большим погрешностям в
случае, когда значения коэффициентов уравнений и свободных членов заданы
приближенно или когда производится округление этих значений в процессе
вычислений.
В первую очередь это относится к случаю, когда матрица, отвечающая основному
определителю (или базисному минору), является плохо обусловленной
(т.
е. когда «малым» изменениям элементов этой матрицы отвечают «большие» изменения
элементов обратной матрицы). Естественно, что в этом случае решение линейной
системы будет неустойчивым
(т. е. «малым» изменениям значений
коэффициентов уравнений и свободных членов будут отвечать «большие» изменения
решения).
Отмеченные обстоятельства приводят к необходимости разработки как других
(отличных от формул Крамера) теоретических алгоритмов отыскания решения, так и
численных методов решения линейных систем.
В §4 гл.4 мы познакомимся с методом регуляризации А.Н. Тихонова
отыскания так называемого нормального
(т. е. наиболее близкого к началу
координат) решения линейной системы.
В гл.6 будут изложены основные сведения о так называемых итерационных
методах
решения линейных систем, позволяющих решать эти системы при помощи
последовательных приближений неизвестных.
Системой m линейных уравнений с n неизвестными называется система вида
где a ij и b i (i =1,…,m ; b =1,…,n ) – некоторые известные числа, а x 1 ,…,x n – неизвестные. В обозначении коэффициентов a ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы 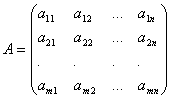 , которую назовём матрицей
системы
.
, которую назовём матрицей
системы
.
Числа, стоящие в правых частях уравнений, b 1 ,…,b m называются свободными членами.
Совокупность n чисел c 1 ,…,c n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c 1 ,…,c n вместо соответствующих неизвестных x 1 ,…,x n .
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной . В противном случае, т.е. если система не имеет решений, то она называется несовместной .
Рассмотрим способы нахождения решений системы.
МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим
матрицу системы  и матрицы столбцы
неизвестных и свободных членов
и матрицы столбцы
неизвестных и свободных членов 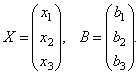
Найдем произведение

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде
 или короче A
∙X=B
.
или короче A
∙X=B
.
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением .
Пусть определитель матрицы отличен от нуля |A | ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A : . Поскольку A -1 A = E и E ∙X = X , то получаем решение матричного уравнения в виде X = A -1 B .
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных . Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B .
Примеры. Решить системы уравнений.

ПРАВИЛО КРАМЕРА
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы .
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
![]()
Доказательство . Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A 11 элемента a 11 , 2-ое уравнение – на A 21 и 3-е – на A 31 :
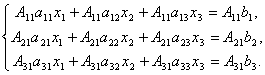
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
Аналогично можно показать, что и .
Наконец несложно заметить, что 
Таким образом, получаем равенство: .
Следовательно, .
Аналогично выводятся равенства и , откуда и следует утверждение теоремы.
Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Примеры. Решить систему уравнений

МЕТОД ГАУССА
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:
 .
.
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x 1 . Для этого второе уравнение разделим на а 21 и умножим на –а 11 , а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а 31 и умножим на –а 11 , а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x 2 . Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x 3 , затем из 2-го уравнения x 2 и, наконец, из 1-го – x 1 .
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
- перестановка строк или столбцов;
- умножение строки на число, отличное от нуля;
- прибавление к одной строке другие строки.
Примеры: Решить системы уравнений методом Гаусса.

Таким образом, система имеет бесконечное множество решений.
Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Нам понадобятся сведения из темы "Система линейных алгебраических уравнений. Основные термины. Матричная форма записи" . В частности, нужны такие понятия, как матрица системы и расширенная матрица системы , поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы - буквой $\widetilde{A}$.
Теорема Кронекера-Капелли
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $\rang A=\rang\widetilde{A}$.
Напомню, что система называется совместной, если она имеет хоть одно решение. Теорема Кронекера-Капелли говорит вот о чём: если $\rang A=\rang\widetilde{A}$, то решение есть; если $\rang A\neq\rang\widetilde{A}$, то данная СЛАУ не имеет решений (несовместна). Ответ на вопрос о количестве этих решений даёт следствие из теоремы Кронекера-Капелли. В формулировке следствия использована буква $n$, которая равна количеству переменных заданной СЛАУ.
Следствие из теоремы Кронекера-Капелли
- Если $\rang A\neq\rang\widetilde{A}$, то СЛАУ несовместна (не имеет решений).
- Если $\rang A=\rang\widetilde{A} < n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
- Если $\rang A=\rang\widetilde{A} = n$, то СЛАУ является определённой (имеет ровно одно решение).
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют - то сколько.
Пример №1
Исследовать СЛАУ $ \left \{\begin{aligned} & -3x_1+9x_2-7x_3=17;\\ & -x_1+2x_2-4x_3=9;\\ & 4x_1-2x_2+19x_3=-42. \end{aligned}\right.$ на совместность. Если СЛАУ совместна, указать количество решений.
Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $\widetilde{A}$, запишем их:
$$ A=\left(\begin{array} {ccc} -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \end{array} \right);\; \widetilde{A}=\left(\begin{array} {ccc|c} -3 & 9 &-7 & 17 \\ -1 & 2 & -4 & 9\\ 4 & -2 & 19 & -42 \end{array} \right). $$
Нужно найти $\rang A$ и $\rang\widetilde{A}$. Для этого есть много способов, некоторые из которых перечислены в разделе "Ранг матрицы" . Обычно для исследования таких систем применяют два метода: "Вычисление ранга матрицы по определению" или "Вычисление ранга матрицы методом элементарных преобразований" .
Способ №1. Вычисление рангов по определению.
Согласно определению, ранг - это наивысший порядок миноров матрицы , среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ - это определитель матрицы $A$, т.е. $\Delta A$. Для вычисления определителя применим формулу №2 из темы "Формулы для вычисления определителей второго и третьего порядков" :
$$ \Delta A=\left| \begin{array} {ccc} -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \end{array} \right|=-21. $$
Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $\rang A=3$.
Нам требуется найти также и $\rang\widetilde{A}$. Давайте посмотрим на структуру матрицы $\widetilde{A}$. До черты в матрице $\widetilde{A}$ находятся элементы матрицы $A$, причём мы выяснили, что $\Delta A\neq 0$. Следовательно, у матрицы $\widetilde{A}$ есть минор третьего порядка, который не равен нулю. Миноров четвёртого порядка матрицы $\widetilde{A}$ составить мы не можем, поэтому делаем вывод: $\rang\widetilde{A}=3$.
Так как $\rang A=\rang\widetilde{A}$, то согласно теореме Кронекера-Капелли система совместна, т.е. имеет решение (хотя бы одно). Чтобы указать количество решений, учтём, что наша СЛАУ содержит 3 неизвестных: $x_1$, $x_2$ и $x_3$. Так как количество неизвестных $n=3$, то делаем вывод: $\rang A=\rang\widetilde{A}=n$, поэтому согласно следствия из теоремы Кронекера-Капелли, система является определённой, т.е. имеет единственное решение.
Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $\Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы .
Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $\Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может - ни одного. Если $\Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.
Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.
Способ №2. Вычисление ранга методом элементарных преобразований.
Подробно это метод описан в соответствующей теме . Мы станем вычислять ранг матрицы $\widetilde{A}$. Почему именно матрицы $\widetilde{A}$, а не $A$? Дело в том, что матрица $A$ является частью матрицы $\widetilde{A}$, поэтому вычисляя ранг матрицы $\widetilde{A}$ мы одновременно найдем и ранг матрицы $A$.
\begin{aligned} &\widetilde{A} =\left(\begin{array} {ccc|c} -3 & 9 &-7 & 17 \\ -1 & 2 & -4 & 9\\ 4 & -2 & 19 & -42 \end{array} \right) \rightarrow \left|\text{меняем местами первую и вторую строки}\right| \rightarrow \\ &\rightarrow \left(\begin{array} {ccc|c} -1 & 2 & -4 & 9 \\ -3 & 9 &-7 & 17\\ 4 & -2 & 19 & -42 \end{array} \right) \begin{array} {l} \phantom{0} \\ r_2-3r_1\\ r_3+4r_1 \end{array} \rightarrow \left(\begin{array} {ccc|c} -1 & 2 & -4 & 9 \\ 0 & 3 &5 & -10\\ 0 & 6 & 3 & -6 \end{array} \right) \begin{array} {l} \phantom{0} \\ \phantom{0}\\ r_3-2r_2 \end{array}\rightarrow\\ &\rightarrow \left(\begin{array} {ccc|c} -1 & 2 & -4 & 9 \\ 0 & 3 &5 & -10\\ 0 & 0 & -7 & 14 \end{array} \right) \end{aligned}
Мы привели матрицу $\widetilde{A}$ к ступенчатому виду . Полученная ступенчатая матрица имеет три ненулевых строки, поэтому её ранг равен 3. Следовательно, и ранг матрицы $\widetilde{A}$ равен 3, т.е. $\rang\widetilde{A}=3$. Делая преобразования с элементами матрицы $\widetilde{A}$ мы одновременно преобразовывали и элементы матрицы $A$, расположенные до черты. Матрица $A$ также приведена к ступенчатому виду: $\left(\begin{array} {ccc} -1 & 2 & -4 \\ 0 & 3 &5 \\ 0 & 0 & -7 \end{array} \right)$. Вывод: ранг матрицы $A$ также равен 3, т.е. $\rang A=3$.
Так как $\rang A=\rang\widetilde{A}$, то согласно теореме Кронекера-Капелли система совместна, т.е. имеет решение. Чтобы указать количество решений, учтём, что наша СЛАУ содержит 3 неизвестных: $x_1$, $x_2$ и $x_3$. Так как количество неизвестных $n=3$, то делаем вывод: $\rang A=\rang\widetilde{A}=n$, поэтому согласно следствия из теоремы Кронекера-Капелли, система определена, т.е. имеет единственное решение.
Какие преимущества второго способа? Главное преимущество - это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса . Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор - это дело вкуса.
Ответ : Заданная СЛАУ совместна и определена.
Пример №2
Исследовать СЛАУ $ \left\{ \begin{aligned} & x_1-x_2+2x_3=-1;\\ & -x_1+2x_2-3x_3=3;\\ & 2x_1-x_2+3x_3=2;\\ & 3x_1-2x_2+5x_3=1;\\ & 2x_1-3x_2+5x_3=-4. \end{aligned} \right.$ на совместность.
Находить ранги матрицы системы и расширенной матрицы системы будем методом элементарных преобразований . Расширенная матрица системы: $\widetilde{A}=\left(\begin{array} {ccc|c} 1 & -1 & 2 & -1\\ -1 & 2 & -3 & 3 \\ 2 & -1 & 3 & 2 \\ 3 & -2 & 5 & 1 \\ 2 & -3 & 5 & -4 \end{array} \right)$. Найдём требуемые ранги, преобразовывая расширенную матрицу системы:
$$ \left(\begin{array} {ccc|c} 1 & -1 & 2 & -1\\ -1 & 2 & -3 & 3 \\ 2 & -3 & 5 & -4 \\ 3 & -2 & 5 & 1 \\ 2 & -1 & 3 & 2 \end{array} \right) \begin{array} {l} \phantom{0}\\r_2+r_1\\r_3-2r_1\\ r_4-3r_1\\r_5-2r_1\end{array}\rightarrow \left(\begin{array} {ccc|c} 1 & -1 & 2 & -1\\ 0 & 1 & -1 & 2 \\ 0 & -1 & 1 & -2 \\ 0 & 1 & -1 & 4 \\ 0 & 1 & -1 & 4 \end{array} \right) \begin{array} {l} \phantom{0}\\\phantom{0}\\r_3-r_2\\ r_4-r_2\\r_5+r_2\end{array}\rightarrow\\ $$ $$ \rightarrow\left(\begin{array} {ccc|c} 1 & -1 & 2 & -1\\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \end{array} \right) \begin{array} {l} \phantom{0}\\\phantom{0}\\\phantom{0}\\ r_4-r_3\\\phantom{0}\end{array}\rightarrow \left(\begin{array} {ccc|c} 1 & -1 & 2 & -1\\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right) $$
Расширенная матрица системы приведена к ступенчатому виду . Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $\rang\widetilde{A}=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $\rang{A}=2$.
Так как $\rang A\neq\rang\widetilde{A}$, то согласно теореме Кронекера-Капелли система несовместна (т.е. не имеет решений).
Ответ : система несовместна.
Пример №3
Исследовать СЛАУ $ \left\{ \begin{aligned} & 2x_1+7x_3-5x_4+11x_5=42;\\ & x_1-2x_2+3x_3+2x_5=17;\\ & -3x_1+9x_2-11x_3-7x_5=-64;\\ & -5x_1+17x_2-16x_3-5x_4-4x_5=-90;\\ & 7x_1-17x_2+23x_3+15x_5=132. \end{aligned} \right.$ на совместность.
Приводим расширенную матрицу системы к ступенчатому виду:
$$ \left(\begin{array}{ccccc|c} 2 & 0 & 7 & -5 & 11 & 42\\ 1 & -2 & 3 & 0 & 2 & 17 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \end{array} \right) \overset{r_1\leftrightarrow{r_3}}{\rightarrow} $$ $$ \rightarrow\left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 2 & 17\\ 2 & 0 & 7 & -5 & 11 & 42\\ -3 & 9 & -11 & 0 & -7 & -64\\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \end{array} \right) \begin{array} {l} \phantom{0}\\ r_2-2r_1 \\r_3+3r_1 \\ r_4+5r_1 \\ r_5-7r_1 \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 2 & 17\\ 0 & 4 & 1 & -5 & 7 & 8\\ 0 & 3 & -2 & 0 & -1 & -13\\ 0 & 7 & -1 & -5 & 6 & -5 \\ 0 & -3 & 2 & 0 & 1 & 13 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\4r_3+3r_2 \\ 4r_4-7r_2 \\ 4r_5+3r_2 \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 2 & 17\\ 0 & 4 & 1 & -5 & 7 & 8\\ 0 & 0 & -11 & 15 & -25 & -76\\ 0 & 0 & -11 & 15 & -25 & -76 \\ 0 & 0 & 11 & -15 & 25 & 76 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\\phantom{0} \\ r_4-r_3 \\ r_5+r_2 \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 2 & 17\\ 0 & 4 & 1 & -5 & 7 & 8\\ 0 & 0 & -11 & 15 & -25 & -76\\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right) $$
Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду . Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $\rang\widetilde{A}=\rang{A}\lt{n}$, то согласно следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.
Ответ : система является неопределённой.
Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.
Пример 1 . Найти общее решение и какое–нибудь частное решение системыРешение
выполняем с помощью калькулятора . Выпишем расширенную и основную матрицы:

Пунктиром отделена основная матрица A. Сверху пишем неизвестные системы, имея в виду возможную перестановку слагаемых в уравнениях системы. Определяя ранг расширенной матрицы, одновременно найдем ранг и основной. В матрице B первый и второй столбцы пропорциональны. Из двух пропорциональных столбцов в базисный минор может попасть только один, поэтому перенесем, например, первый столбец за пунктирную черту с обратным знаком. Для системы это означает перенос членов с x 1 в правую часть уравнений.

Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы. Работаем с первой строкой: умножим первую строку матрицы на (-3) и прибавим ко второй и третьей строкам по очереди. Затем первую строку умножим на (-2) и прибавим к четвертой.

Вторая и третья строки пропорциональны, следовательно, одну из них, например вторую, можно вычеркнуть. Это равносильно вычеркиванию второго уравнения системы, так как оно является следствием третьего.

Теперь работаем со второй строкой: умножим ее на (-1) и прибавим к третьей.

Минор, обведенный пунктиром, имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на главной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rangA = rangB = 3 .
Минор  является базисным. В него вошли коэффициенты при неизвестных x 2 , x 3 , x 4 , значит, неизвестные x 2 , x 3 , x 4 – зависимые, а x 1 , x 5 – свободные.
является базисным. В него вошли коэффициенты при неизвестных x 2 , x 3 , x 4 , значит, неизвестные x 2 , x 3 , x 4 – зависимые, а x 1 , x 5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор (что соответствует пункту 4 приведенного выше алгоритма решения).

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид

x 4 =3-4x 5 , x 3 =3-4x 5 -2x 4 =3-4x 5 -6+8x 5 =-3+4x 5
x 2 =x 3 +2x 4 -2+2x 1 +3x 5 = -3+4x 5 +6-8x 5 -2+2x 1 +3x 5 = 1+2x 1 -x 5
Получили соотношения, выражающие зависимые переменные x 2 , x 3 , x 4 через свободные x 1 и x 5 , то есть нашли общее решение:

Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Найдем два частных решения:
1) пусть x 1 = x 5 = 0, тогда x 2 = 1, x 3 = -3, x 4 = 3;
2) положим x 1 = 1, x 5 = -1, тогда x 2 = 4, x 3 = -7, x 4 = 7.
Таким образом, нашли два решения: (0,1,-3,3,0) – одно решение, (1,4,-7,7,-1) – другое решение.
Пример 2
. Исследовать совместность, найти общее и одно частное решение системы

Решение
. Переставим первое и второе уравнения, чтобы иметь единицу в первом уравнении и запишем матрицу B.

Получим нули в четвертом столбце, оперируя первой строкой:

Теперь получим нули в третьем столбце с помощью второй строки:

 Третья и четвертая строки пропорциональны, поэтому одну из них можно вычеркнуть, не меняя ранга:
Третья и четвертая строки пропорциональны, поэтому одну из них можно вычеркнуть, не меняя ранга:
Третью строку умножим на (–2) и прибавим к четвертой:

Видим, что ранги основной и расширенной матриц равны 4, причем ранг совпадает с числом неизвестных, следовательно, система имеет единственное решение:
-x 1 =-3 → x 1 =3; x 2 =3-x 1 → x 2 =0; x 3 =1-2x 1 → x 3 =5.
x 4 = 10- 3x 1 – 3x 2 – 2x 3 = 11.
Пример 3
. Исследовать систему на совместность и найти решение, если оно существует.

Решение
. Составляем расширенную матрицу системы.

 Переставляем первые два уравнения, чтобы в левом верхнем углу была 1:
Переставляем первые два уравнения, чтобы в левом верхнем углу была 1:
Умножая первую строку на (-1), складываем ее с третьей:

Умножим вторую строку на (-2) и прибавим к третьей:

Система несовместна, так как в основной матрице получили строку, состоящую из нулей, которая вычеркивается при нахождении ранга, а в расширенной матрице последняя строка останется, то есть r B > r A .
Задание
. Исследовать данную систему уравнений на совместность и решить ее средствами матричного исчисления .
Решение
Пример
. Доказать совместимость системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса ; 2) методом Крамера . (ответ ввести в виде: x1,x2,x3)
Решение :doc :doc :xls
Ответ:
2,-1,3.
Пример
. Дана система линейных уравнений. Доказать ее совместность. Найти общее решение системы и одно частное решение.
Решение
Ответ:
x 3 = - 1 + x 4 + x 5 ; x 2 = 1 - x 4 ; x 1 = 2 + x 4 - 3x 5
Задание
. Найти общее и частное решения каждой системы.
Решение.
Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Здесь матрица А выделена жирным шрифтом.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-3). Добавим 3-ую строку к 2-ой:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rang(A) = rang(B) = 3. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной .
Этот минор является базисным. В него вошли коэффициенты при неизвестных x 1 ,x 2 ,x 3 , значит, неизвестные x 1 ,x 2 ,x 3 – зависимые (базисные), а x 4 ,x 5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
27x 3 =
- x 2 + 13x 3 = - 1 + 3x 4 - 6x 5
2x 1 + 3x 2 - 3x 3 = 1 - 3x 4 + 2x 5
Методом исключения неизвестных находим:
Получили соотношения, выражающие зависимые переменные x 1 ,x 2 ,x 3 через свободные x 4 ,x 5 , то есть нашли общее решение :
x 3 = 0
x 2 = 1 - 3x 4 + 6x 5
x 1 = - 1 + 3x 4 - 8x 5
неопределенной , т.к. имеет более одного решения.
Задание
. Решить систему уравнений.
Ответ
:x 2 = 2 - 1.67x 3 + 0.67x 4
x 1 = 5 - 3.67x 3 + 0.67x 4
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной