Naďalej sa zaoberáme sústavami lineárnych rovníc. Doteraz sme sa pozerali na systémy, ktoré majú jediné riešenie. Takéto systémy je možné vyriešiť akýmkoľvek spôsobom: substitučná metóda(„Škola“), podľa Cramerových vzorcov, maticová metóda, Gaussova metóda... V praxi sú však rozšírené ďalšie dva prípady, keď:
1) systém je nekompatibilný (nemá žiadne riešenia);
2) systém má nekonečne veľa riešení.
Pre tieto systémy sa používa najuniverzálnejšia zo všetkých metód riešenia - Gaussova metóda... V skutočnosti metóda „škola“ povedie k odpovedi, ale vo vyššej matematike je zvykom používať gaussovskú metódu postupného odstraňovania neznámych. Tí, ktorí nie sú oboznámení s algoritmom Gaussovej metódy, najskôr si preštudujte lekciu Gaussova metóda
Samotné transformácie elementárnej matice sú úplne rovnaké, rozdiel bude na konci riešenia. Pozrime sa najskôr na niekoľko príkladov, keď systém nemá žiadne riešenia (nekonzistentné).
Príklad 1
Čo vám v tomto systéme okamžite padne do oka? Počet rovníc je menší ako počet premenných. Existuje veta, ktorá hovorí: „Ak je počet rovníc v systéme menší ako počet premenných, potom je systém buď nekonzistentný, alebo má nekonečne veľa riešení. “ A zostáva len zistiť.
Začiatok riešenia je úplne obyčajný - zapíšeme si rozšírenú maticu systému a pomocou elementárnych transformácií ju uvedieme do postupnej podoby:
(jeden). V ľavom hornom kroku musíme získať (+1) alebo (–1). V prvom stĺpci také čísla nie sú, takže preskupenie riadkov nič nezmení. Jednotka bude musieť byť organizovaná nezávisle a to je možné niekoľkými spôsobmi. Toto sme urobili. Do prvého riadku pridajte tretí riadok vynásobený (–1).
(2). Teraz dostaneme dve nuly v prvom stĺpci. Do druhého riadku pridáme prvý riadok vynásobený 3. Do tretieho riadku pridáme prvý riadok vynásobený 5.
(3). Po vykonanej transformácii je vždy vhodné pozrieť sa a je možné výsledné riadky zjednodušiť? Môcť. Rozdeľte druhý riadok o 2 a súčasne získajte požadované (–1) v druhom kroku. Tretí riadok vydelíme (–3).
(4). Pridajte druhý riadok k tretiemu riadku. Pravdepodobne každý venoval pozornosť zlej línii, ktorá sa ukázala v dôsledku elementárnych transformácií:
... Je jasné, že to tak nemôže byť.
Výslednú maticu skutočne prepíšeme
späť do systému lineárnych rovníc:
Ak je v dôsledku elementárnych transformácií reťazec formulára , kdeλ - číslo iné ako nula, potom je systém nekompatibilný (nemá žiadne riešenia).
Ako môžem zaznamenať koniec úlohy? Musíte si zapísať vetu:
"V dôsledku elementárnych transformácií bol získaný reťazec formulára, kde λ ≠ 0 “. Odpoveď: "Systém nemá žiadne riešenia (nekonzistentné)."
Vezmite prosím na vedomie, že v tomto prípade neexistuje žiadne spätné sledovanie gaussovského algoritmu, neexistujú žiadne riešenia a jednoducho nie je čo nájsť.
Príklad 2
Vyriešte sústavu lineárnych rovníc 
Toto je príklad riešenia pre domácich majstrov. Kompletné riešenie a odpoveď na konci tutoriálu.
Opäť pripomíname, že váš rozhodovací kurz sa môže líšiť od nášho rozhodovacieho kurzu, Gaussova metóda neurčuje jednoznačný algoritmus, poradie akcií a samotné akcie musíte v každom prípade hádať nezávisle.
Ďalšia technická vlastnosť riešenia: elementárne transformácie je možné zastaviť okamžite, akonáhle sa objavil riadok formulára, kde λ ≠ 0 ... Uvažujme podmienený príklad: predpokladajme, že po úplne prvej transformácii sa získa matica
.
Táto matica ešte nebola zredukovaná na stupňovitú formu, ale nie sú potrebné ďalšie elementárne transformácie, pretože sa objavil riadok formy, kde λ ≠ 0 ... Mali by ste okamžite odpovedať, že systém je nekompatibilný.
Ak systém lineárnych rovníc nemá žiadne riešenia, je to pre študenta takmer dar, pretože sa získa krátke riešenie, niekedy doslova v 2 až 3 krokoch. Ale všetko v tomto svete je vyvážené a problém, v ktorom má systém nekonečne veľa riešení, je len dlhší.
Príklad 3:
Vyriešte sústavu lineárnych rovníc
Existujú 4 rovnice a 4 neznáme, takže systém môže mať buď jedno riešenie, alebo žiadne riešenia, alebo môže mať nekonečne veľa riešení. Nech je to akokoľvek, ale Gaussova metóda nás aj tak dovedie k odpovedi. Toto je jeho univerzálnosť.
Začiatok je opäť štandardný. Zapíšeme si rozšírenú maticu systému a pomocou elementárnych transformácií ju uvedieme do postupnej podoby:
To je všetko a báli ste sa.
(jeden). Upozorňujeme, že všetky čísla v prvom stĺpci sú deliteľné 2, takže v ľavom hornom kroku sme spokojní aj s dvoma. Do druhého riadku pridajte prvý riadok vynásobený (–4). Do tretieho riadka pridajte prvý riadok vynásobený (–2). Do štvrtého riadka pridajte prvý riadok vynásobený (–1).
Pozor! Mnohí môžu byť v pokušení zo štvrtej rady odčítať prvá línia. To sa dá urobiť, ale nie je to nevyhnutné, skúsenosti ukazujú, že pravdepodobnosť chyby vo výpočtoch sa niekoľkokrát zvyšuje. Stačí pridať: do štvrtého riadka pridajte prvý riadok vynásobený (–1) - presne!
(2). Posledné tri riadky sú proporcionálne, dva z nich je možné vymazať. Tu sa opäť musíte ukázať zvýšená pozornosť, sú však riadky skutočne proporcionálne? Pre istotu nie je nadbytočné vynásobiť druhý riadok (–1) a rozdeliť štvrtý riadok o 2, výsledkom sú tri rovnaké riadky. A až potom odstráňte dvoch z nich. V dôsledku elementárnych transformácií sa rozšírená matica systému zredukuje na stupňovitú formu:
Pri vypĺňaní úlohy v zošite je vhodné kvôli prehľadnosti urobiť rovnaké poznámky ceruzkou.
Prepíšeme zodpovedajúci systém rovníc: 
Jediné riešenie systému tu nezapácha ako „obvyklé“. Zlá linka kde λ ≠ 0, tiež nie. To znamená, že toto je tretí zostávajúci prípad - systém má nekonečne veľa riešení.
Nekonečné množstvo systémových riešení je stručne napísaných vo forme tzv celkové systémové riešenie.
Všeobecné riešenie systému nachádzame pomocou reverzného pohybu Gaussovej metódy. V prípade sústav rovníc s nekonečným súborom riešení sa objavujú nové koncepty: "Základné premenné" a "Voľné premenné"... Najprv definujme, aké premenné máme základné, a ktoré premenné - zadarmo... Nie je potrebné podrobne vysvetľovať pojmy lineárnej algebry, stačí si uvedomiť, že existujú základné premenné a voľné premenné.
Základné premenné vždy „sedia“ striktne na krokoch matice... V tomto prípade ide o základné premenné X 1 a X 3 .
Voľné premenné sú všetko zostávajúce premenné, ktoré nedostali priečku. V našom prípade existujú dve z nich: X 2 a X 4 - voľné premenné.
Teraz potrebujete všetkyzákladné premenné vyjadriť iba cezvoľné premenné... Rub Gaussovho algoritmu tradične funguje zdola nahor. Z druhej rovnice systému vyjadríme základnú premennú X 3:
Teraz sa pozrime na prvú rovnicu: 
... Najprv doňho dosadíme nájdený výraz:
Zostáva vyjadriť základnú premennú X 1 prostredníctvom voľných premenných X 2 a X 4:
Nakoniec sme dostali to, čo potrebujeme - všetky základné premenné ( X 1 a X 3) vyjadrené iba cez voľné premenné ( X 2 a X 4):
Všeobecné riešenie je v skutočnosti pripravené:
.
Ako správne zapísať všeobecné riešenie? Voľné premenné sú v prvom rade zapísané do všeobecného riešenia „samy“ a striktne na svoje miesta. V tomto prípade bezplatné premenné X 2 a X 4 by malo byť napísané na druhej a štvrtej pozícii:
.
Získané výrazy pre základné premenné a samozrejme musíte napísať na prvú a tretiu pozíciu:
Zo všeobecného riešenia systému ich môžete nájsť nekonečne veľa súkromné riešenia... Je to velmi jednoduche Voľné premenné X 2 a X 4 sa nazývajú tak, pretože môžu byť dané akékoľvek koncové hodnoty... Najpopulárnejšie hodnoty sú nulové, pretože toto je najľahší spôsob, ako získať konkrétne riešenie.
Striedanie ( X 2 = 0; X 4 = 0) do všeobecného riešenia dostaneme jedno z konkrétnych riešení:
alebo je konkrétne riešenie zodpovedajúce voľným premenným v hodnotách ( X 2 = 0; X 4 = 0).
Jednotky sú ďalším sladkým párom, náhradníkom ( X 2 = 1 a X 4 = 1) do všeobecného riešenia:
(-1; 1; 1; 1) je ďalšie konkrétne riešenie.
Je ľahké vidieť, že systém rovníc má nekonečne veľa riešení, pretože môžeme dávať bezplatné premenné akýkoľvek hodnoty.
Každý konkrétne riešenie musí vyhovovať každému rovnica systému. Toto je základ pre „rýchlu“ kontrolu správnosti riešenia. Vezmite napríklad konkrétne riešenie (-1; 1; 1; 1) a nahraďte ho ľavou stranou každej rovnice pôvodného systému:
Všetko by malo do seba zapadať. A pri každom konkrétnom rozhodnutí, ktoré dostanete - všetko by malo tiež súhlasiť.
Presne povedané, kontrola konkrétneho riešenia niekedy klame, t.j. niektoré konkrétne riešenie môže uspokojiť každú rovnicu systému, ale samotné všeobecné riešenie je v skutočnosti nájdené nesprávne. Preto je kontrola všeobecného riešenia v prvom rade dôkladnejšia a spoľahlivejšia.
Ako skontrolovať výsledné všeobecné riešenie 
?
Nie je to ťažké, ale vyžaduje si to veľa časovo náročných transformácií. Musíte mať výrazy základné premenné, v tomto prípade 
a nahraďte ich na ľavej strane každej rovnice systému.
Na ľavej strane prvej rovnice systému:
Získa sa pravá strana počiatočnej prvej rovnice systému.
Na ľavej strane druhej rovnice systému:
Získa sa pravá strana pôvodnej druhej rovnice systému.
A ďalej - na ľavú stranu tretej a štvrtej rovnice systému. Táto kontrola trvá dlhšie, ale zaručuje stopercentnú správnosť celkového riešenia. Pri niektorých úlohách je navyše potrebné práve overenie všeobecného riešenia.
Príklad 4:
Vyriešte systém pomocou Gaussovej metódy. Nájdite všeobecné riešenie a dve konkrétne. Skontrolujte všeobecné riešenie.
Toto je príklad riešenia pre domácich majstrov. Tu je, mimochodom, opäť počet rovníc menší ako počet neznámych, čo znamená, že je okamžite zrejmé, že systém bude buď nekompatibilný, alebo s nekonečným súborom riešení.
Príklad 5:
Vyriešte sústavu lineárnych rovníc. Ak má systém nekonečne veľa riešení, nájdite dve konkrétne riešenia a skontrolujte všeobecné riešenie
Riešenie: Zapíšeme si rozšírenú maticu systému a pomocou elementárnych transformácií ju uvedieme do postupnej podoby:
(jeden). Pridajte prvý riadok do druhého riadku. Do tretieho riadku pridáme prvý riadok vynásobený 2. Do štvrtého riadku pridáme prvý riadok vynásobený 3.
(2). Do tretieho riadka pridajte druhý riadok vynásobený (–5). Do štvrtého riadka pridajte druhý riadok vynásobený (–7).
(3). Tretí a štvrtý riadok sú rovnaké, jeden z nich odstránime. Tu je taká krása:
Základné premenné sedia na priečky, preto základné premenné.
Existuje iba jedna voľná premenná, ktorá tu nedostala krok :.
(4). Reverzný pohyb. Vyjadrime základné premenné vo forme voľnej premennej:
Z tretej rovnice:
Zvážte druhú rovnicu a nahraďte do nej nájdený výraz:
, 
, ,
Zvážte prvú rovnicu a nahraďte nájdené výrazy a do nej:
Všeobecné riešenie pre jednu voľnú premennú teda je X 4:
Ešte raz, ako to vzniklo? Voľná premenná X 4 sedí sám na svojom právoplatnom štvrtom mieste. Výsledné výrazy pre základné premenné sú tiež na svojich miestach.
Hneď skontrolujeme všeobecné riešenie.
Základné premenné nahradíme na ľavej strane každej rovnice systému:
Získajú sa zodpovedajúce pravé strany rovníc, takže sa nájde správne všeobecné riešenie.
Teraz z nájdeného spoločného riešenia 
dostávame dve konkrétne riešenia. Všetky premenné sú tu vyjadrené prostredníctvom jednej voľná premenná x 4. Nie je potrebné si lámať hlavu.
Nechaj byť X 4 = 0, potom 
- prvé konkrétne riešenie.
Nechaj byť X 4 = 1, potom 
- ešte jedno konkrétne riešenie.
Odpoveď: Spoločné rozhodnutie: ... Súkromné riešenia:
a.
Príklad 6:
Nájdite všeobecné riešenie sústavy lineárnych rovníc.
Všeobecné rozhodnutie sme už skontrolovali, odpovedi sa dá dôverovať. Váš spôsob rozhodovania sa môže líšiť od nášho spôsobu rozhodovania. Ide o to, aby sa spoločné rozhodnutia zhodovali. Pravdepodobne si mnohí všimli nepríjemný moment v riešeniach: veľmi často sme počas opačného priebehu Gaussovej metódy museli pohrávať s obyčajné zlomky... V praxi to platí, prípady, keď neexistujú žiadne zlomky, sú oveľa menej časté. Buďte pripravení mentálne, a čo je najdôležitejšie, technicky.
Pozastavme sa nad vlastnosťami riešenia, ktoré sa v riešených príkladoch nenašli. Všeobecné riešenie systému môže niekedy zahŕňať konštantu (alebo konštanty).
Všeobecným riešením je napríklad :. Tu sa jedna zo základných premenných rovná konštantnému číslu :. Nie je na tom nič exotické, to sa stáva. Je zrejmé, že v tomto prípade bude akékoľvek konkrétne riešenie obsahovať A na prvej pozícii.
Zriedka, ale existujú systémy, v ktorých počet rovníc je väčší ako počet premenných... Gaussova metóda však funguje za najtvrdších podmienok. Rozšírenú maticu systému je potrebné pokojne zredukovať na stupňovitú formu podľa štandardného algoritmu. Takýto systém môže byť nekonzistentný, môže mať nekonečne veľa riešení a napodiv môže mať jediné riešenie.
Zopakujme si v našich radách - aby ste sa pri riešení systému pomocou Gaussovej metódy cítili príjemne, mali by ste si vyplniť ruku a vyriešiť najmenej tucet systémov.
Riešenia a odpovede:
Príklad 2:
Riešenie:Zapíšeme si rozšírenú maticu systému a pomocou elementárnych transformácií ju uvedieme do postupnej podoby.
Vykonané elementárne transformácie:
(1) Prvý a tretí riadok sa prehodia.
(2) Do druhého riadku bol pridaný prvý riadok vynásobený (–6). Prvý riadok vynásobený (–7) bol pridaný do tretieho riadka.
(3) Druhý riadok vynásobený (–1) bol pridaný do tretieho riadka.
Výsledkom elementárnych transformácií je reťazec formulára, kde λ ≠ 0 .To znamená, že systém je nekompatibilný.Odpoveď: žiadne riešenia.
Príklad 4:
Riešenie:Zapíšeme si rozšírenú maticu systému a pomocou elementárnych transformácií ju uvedieme do postupnej podoby:
Vykonané konverzie:
(jeden). Do druhého riadku bol pridaný prvý riadok vynásobený číslom 2. Do tretieho riadku bol pridaný prvý riadok vynásobený číslom 3.
Na druhý krok nie je nikto a transformácia (2) je zameraná na jeho získanie.
(2). Tretí riadok bol pridaný k druhému riadku vynásobený –3.
(3). Druhý a tretí riadok boli vymenené (výsledné -1 preusporiadané do druhého kroku)
(4). Tretí riadok bol pridaný k druhému riadku vynásobený 3.
(päť). Znak prvých dvoch riadkov bol zmenený (vynásobený –1), tretí riadok bol vydelený 14.
Vzad:
(jeden). Tu - základné premenné (ktoré sú na krokoch) a - voľné premenné (kto nedostal ani krok).
(2). Vyjadrime základné premenné vo forme voľných premenných:
Z tretej rovnice: .
(3). Zoberme si druhú rovnicu:, konkrétne riešenia:
Odpoveď: Spoločné rozhodnutie: 
Komplexné čísla
V tejto časti sa zoznámime s konceptom komplexné číslo, zvážiť algebraické, trigonometrický a ukážková forma komplexné číslo. Naučíme sa tiež vykonávať akcie so zložitými číslami: sčítanie, odčítanie, násobenie, delenie, umocňovanie a extrakcia koreňov.
Na zvládnutie komplexných čísel nepotrebujete žiadne špeciálne znalosti z kurzu vyššej matematiky a materiál má k dispozícii dokonca aj študent. Stačí byť schopný vykonávať algebraické operácie s „obyčajnými“ číslami a pamätať si trigonometriu.
Pripomeňme si najskôr „obyčajné“ čísla. V matematike sa im hovorí množina reálnych čísel a označené písmenom R, alebo R (zahustené). Všetky skutočné čísla sú na známom číselnom rade:
Spoločnosť reálnych čísel je veľmi pestrá - tu existujú celé čísla, zlomky a iracionálne čísla. V tomto prípade každý bod numerickej osi nevyhnutne zodpovedá nejakému skutočnému číslu.
Hľadanie riešení pre lineárny systémPrenosné aplikácie pre Windows na Bodrenko.com
§2. Hľadanie riešení pre lineárny systém
Kroneckerova-Capelliho veta vytvára potrebnú a dostatočnú podmienku kompatibility lineárneho systému, ale neposkytuje spôsob, ako nájsť riešenia pre tento systém.
V tejto časti budeme hľadať riešenia lineárnej sústavy (3.1). Najprv zvážime najjednoduchší prípad kvadratickej sústavy lineárnych rovníc s nenulovým determinantom základnej matice a potom pristúpime k nájdeniu množiny všetkých riešení všeobecnej lineárnej sústavy formy (3.1).
1. Kvadratický systém lineárnych rovníc s nenulovým determinantom hlavnej matice. Nech je daný kvadratický systém lineárnych rovníc
s nenulovým determinantom Δ hlavnej matice
Dokážme, že takýto systém má, a navyše, jedinečné riešenie, a nájdeme toto riešenie. Najprv dokážeme, že systém (3.10) môže mať iba jedno riešenie (t. J. Dokážeme jedinečnosť riešenia systému (3.10) za predpokladu jeho existencie).
Predpokladajme, že existuje niekoľko n čísel x 1, x 2, ..., xn takých, že keď sú tieto čísla nahradené systémom (3.10), všetky rovnice tohto systému sa zmenia na identity (tj. Existuje riešenie systému (3,10) x 1, x 2, ..., x n). Potom vynásobením identít (3.10) algebraickými doplnkami A 1j, A 2j, ..., A nj prvkov j-ro stĺpca determinantu Δ matice (3.11) a následným sčítaním výsledných identít získať (pre akékoľvek číslo j, ktoré sa rovná 1, 2, ..., n)
Berúc do úvahy, že súčet súčinov prvkov i-tého stĺpca zodpovedajúcimi algebraickými doplnkami prvkov stĺpca j-ro sa rovná nule pre i ≠ j a rovná sa determinantu Δ matice (3,11 ) pre i = j (pozri vlastnosť 4 ° z pododdielu 4 § 2 Ch. 1) získame z poslednej rovnosti
x j Δ = b 1 A 1j + b 2 A 2j + ... + b n A nj. (3.12)
Označme symbolomΔ
j (b i ) (alebo stručnejšie symbolΔ
j ) determinant získaný z determinantuΔ
hlavnej matice (3.11) nahradením jej j -tého stĺpca stĺpcom voľných výrazov b 1
, b 2
, ..., b n (všetky ostatné stĺpce zostanú nezmenené
Δ
).
Všimnite si toho, že na pravej strane (3.12) je presne determinant Δ j (bi) (na to, aby ste sa presvedčili, stačí napísať rozšírenie determinantu Δ j (bi) z hľadiska prvkov v stĺpci) a táto rovnosť má formu
Δ x j = Δ j (3,13)
Pretože determinant Δ matice (3.11) je nenulový, rovnosti (3.13) sú ekvivalentné vzťahom
Takže sme to dokázali ak riešenie x 1
, X 2
, ..., NS n systém (3.10) s determinantomΔ
hlavnej matice (3.11) existuje nula, potom je toto riešenie jednoznačne určené vzorcami (3.14).
Vzorce (3.14) sa nazývajú Cramerove vzorce.
Ešte raz zdôrazňujeme, že Cramerove vzorce sme zatiaľ získali za predpokladu existencie riešenia a dokazujeme jeho jedinečnosť.
Zostáva dokázať existenciu riešenia systému (3.10). Na to stačí na základe Kroneckerovej-Capelliho vety dokázať, že hodnosť hlavnej matice (3,11) sa rovná hodnosti rozšírenej matice (existuje aj iný spôsob, ako dokázať existenciu riešenia systému (3.10), ktorá spočíva v kontrole, či čísla x 1, x 2, ..., х n, definované Cramerovými vzorcami (3.14), prevádzajú všetky rovnice systému (3.10) na identity)
ale je to zrejmé, pretože na základe vzťahu Δ ≠ 0 je hodnosť hlavnej matice rovná n a hodnosť rozšírenej matice (3.15) obsahujúcej n riadkov nemôže byť väčšia ako n, a preto je rovnaká do hodnosti hlavnej matice.
To dokazuje úplne to kvadratický systém lineárnych rovníc (3.10) s nenulovým determinantom základnej matice má, a navyše jedinečné riešenie určené Cramerovými vzorcami (3.14).
Tvrdenie, ktoré sme dokázali, je ešte jednoduchšie stanoviť maticovým spôsobom. Aby sme to urobili, nahradíme (ako v pododdiele 1 § 1) systém (3.10) ekvivalentnou maticovou rovnicou
AX = B, (3,16)
kde A je hlavná matica systému (3.11) a X a B sú stĺpce,
prvý z nich sa určí a druhý je daný.
Pretože determinant Δ matice A je nenulový, potom existuje inverzná matica A -1 (pozri časť 7, časť 2, kapitolu 1).
Predpokladajme, že existuje riešenie systému (3.10), t.j. existuje stĺpec X, ktorý robí maticovú rovnicu (3.16) identitou. Vynásobením uvedenej identity vľavo inverznou maticou А -1 budeme mať
A -1 (AX) = A -1 B. (3.17)
Teraz vezmime do úvahy, že na základe kombinačnej vlastnosti súčinu troch matíc (pozri pododdiel 2 § 1 Ch. 1) a na základe vzťahu A -1 A = E, kde E je matica identity (pozri § 7 § 2 Ch. 1), A -1 (AX) = (A -1 A) X = EX = X, takže dostaneme z (3.17)
X = A -1 B. (3,18)
Rozšírenie rovnosti (3.18) a zohľadnenie formy inverznej matice (pozri vzorec A.41) z oddielu 7, oddielu 2, kap. 1), získame Cramerove vzorce pre prvky stĺpca X.
Dokázali sme teda, že ak existuje riešenie maticovej rovnice (3.16), potom je jedinečne určené vzťahom (3.18), ktorý je ekvivalentný Cramerovým vzorcom.
Je ľahké skontrolovať, či stĺpec X definovaný vzťahom (3.18) je skutočne riešením maticovej rovnice (3.16),
to znamená, že keď je nahradený do tejto rovnice, zmení ju na identitu. Ak je stĺpec X definovaný rovnosťou (3,18), potom AX = A (A -1 B) = (AA -1) B = EB = B.
Ak je teda determinant Δ matice A nenulový (to znamená, že ak je táto matica nedegenerovaná), potom existuje a navyše existuje jedinečné riešenie maticovej rovnice (3.16), definované vzťahom (3.18), ekvivalent k Cramerovým vzorcom.
Príklad. Nájdeme riešenie kvadratickej sústavy lineárnych rovníc
s nenulovým determinantom hlavnej matice
Pretože
potom má podľa Cramerových vzorcov jediné riešenie uvažovaného systému tvar x 1 = 1, x 2 = 2, x 3 = 3, x 4 = 4.
Hlavný význam Cramerových vzorcov je, že poskytujú explicitný výraz na riešenie kvadratického systému lineárnych rovníc (s nenulovým determinantom) z hľadiska koeficientov rovníc a voľných výrazov. Praktické používanie Cramerových vzorcov je spojené s dosť ťažkopádnymi výpočtami (na vyriešenie sústavy n rovníc s n neznámym je potrebné vypočítať (n + 1) determinant n -tého rádu). K tomu treba dodať, že ak sú koeficienty rovníc a voľných výrazov len približné hodnoty akýchkoľvek nameraných fyzikálnych veličín alebo sú zaokrúhlené v procese výpočtov, potom použitie Cramerových vzorcov môže viesť k veľkým chybám a v niektoré prípady sú nevhodné.
V oddiele 4, kapitole 4, metóda legalizácie spôsobená A.N. Tichonov a umožňuje vám nájsť riešenie lineárneho systému s presnosťou zodpovedajúcou presnosti zadania matice koeficientov rovníc a stĺpca voľných výrazov a v Ch. 6 dáva predstavu o takzvaných iteračných metódach riešenia lineárnych systémov, ktoré umožňujú riešiť tieto systémy pomocou postupných aproximácií neznámych.
Na záver poznamenávame, že v tomto podsekcii sme z úvah vylúčili prípad miznutia determinantu Δ hlavnej matice systému (3.10). Tento prípad bude obsiahnutý vo všeobecnej teórii systémov m lineárnych rovníc s n neznámych, predstavenej v nasledujúcom pododdiele.
2. Nájdenie všetkých riešení všeobecného lineárneho systému. Uvažujme teraz o všeobecnom systéme m lineárnych rovníc s n neznámych (3.1). Predpokladajme, že tento systém je konzistentný a že poradie jeho hlavných a rozšírených matíc je rovné r. Bez straty všeobecnosti môžeme predpokladať, že základná menšina hlavnej matice (3.2) je v ľavom hornom rohu tejto matice (všeobecný prípad sa na tento prípad redukuje permutáciou rovníc a neznámych v systéme (3.1)).
Potom sú prvé r riadky hlavnej matice (3.2) a rozšírenej matice (3.8) základnými radmi týchto matíc (pretože rady hlavnej a rozšírenej matice sú obidve rovné r, bázová menšina hlavnej matice bude súčasne základom menšej rozšírenej matice) a podľa vety 1.6 o základnej menšej časti je každý z riadkov rozšírenej matice (1,8), počínajúc (r + 1), lineárnou kombináciou prvých r riadkov tejto matice.
Pokiaľ ide o systém (3.1), znamená to, že každá z rovníc tohto systému, počínajúc (r + 1) rovnicou, je lineárnou kombináciou (tj. Dôsledkom) prvých r rovníc tohto systému ( t.j. akékoľvek riešenie prvých r rovníc systému (3.1) sa zmení na identity a všetky nasledujúce rovnice tohto systému).
Stačí teda nájsť všetky riešenia iba pre prvé r rovnice systému (3.1). Zvážte prvé r rovnice systému (3.1) a napíšte ich do formulára
Ak dáme neznámym xr + 1, ..., xn úplne ľubovoľné hodnoty cr + 1, ..., cn, potom sa systém (1.19) zmení na kvadratický systém r lineárnych rovníc pre r neznámych x 1, x 2, ..., х r a determinantom základnej matice tohto systému je nenulová základná menšina matice (3.2). Na základe výsledkov predchádzajúcej časti má tento systém (3.19) jedinečné riešenie definované Cramerovými vzorcami, tj. Pre ľubovoľne zvolené cr + 1, ..., cn existuje jedinečná zbierka r čísel c 1, ..., cr, prevod všetkých rovníc systému (3.19) na identity a definované Cramerovými vzorcami.
Aby sme napísali toto jedinečné riešenie, súhlasíme s tým, že symbolom M j (di) označíme determinant získaný zo základnej molárnej M matice (3.2) nahradením jeho stĺpca j-ro stĺpcom s číslami d 1, d 2, ..., di, ..., dr (všetky ostatné stĺpce M zostanú nezmenené). Potom zapísaním riešenia systému (3.19) pomocou Cramerových vzorcov a použitím lineárnej vlastnosti determinantu získame
Vzorce (3.20) vyjadrujú hodnoty neznámych xj = cj (j = 1, 2, ......, r) prostredníctvom koeficientov neznámych, voľných výrazov a ľubovoľne daných parametrov s r + 1,. ..., s n.
Dokážme to vzorce (3.20) obsahujú akékoľvek riešenie systému (3.1)... Skutočne nech je c (0) 1, c (0) 2, ..., c (0) r, c (0) r + 1, ..., c (0) n ľubovoľné riešenie uvedeného systému . Potom je to aj riešenie systému (3.19). Ale zo systému (3.19) sú veličiny c (0) 1, c (0) 2, ..., c (0) r určené ako veličiny c (0) r + 1, ..., c (0) n jedinečne a presne podľa Cramerových vzorcov (3,20). Preto pre c r + 1 = c (0)
r + 1, ..., s n = c (0)
n
vzorce (3.20) nám poskytujú uvažované riešenie c (0)
1
, c (0)
2
, ..., c (0)
r , c (0)
r + 1, ..., c (0)
n .
Komentovať. Ak sa hodnosť r hlavných a rozšírených matíc systému (3.1) rovná počtu neznámych n, potom v tomto prípade vzťahy (3.20) prejdú na vzorce
určenie jedinečného riešenia systému (3.1). Systém (3.1) má teda jedinečné riešenie (tj. Je definitívne) za predpokladu, že hodnosť r jeho hlavných a rozšírených matíc je rovnaká ako počet neznámych n (a je menší alebo rovný počtu rovníc m).
Príklad. Nájdite všetky riešenia lineárneho systému
Je ľahké overiť, že hodnosť hlavnej aj rozšírenej matice tohto systému je rovná dvom (tj. Tento systém je konzistentný), a môžeme predpokladať, že základné molálne písmeno M je v ľavom hornom rohu hlavnej matice. , tj 
... Ale potom, keď vyradíme posledné dve rovnice a nastavíme ľubovoľne 3 a 4, dostaneme systém
x 1 - x 2 = 4 - c 3 + c 4,
x 1 + x 2 = 8 - 2c 3 - 3c 4,
z ktorého na základe Cramerových vzorcov získame hodnoty
x 1 = c 1 = 6 - 3/2 c 3 - c 4, x 2 = c 2 = 2 - 1/2 c 3 - 2c 4. (3,22)
Takže štyri čísla
(6 - 3/2 c 3 - c 4, 2 - 1/2 c 3 - 2c 4, c 3, c 4) (3,23)
náhodne nastavené hodnoty c 3 a c 4 tvoria riešenie systému (3.21) a riadok (3.23) obsahuje všetky riešenia tohto systému.
3. Vlastnosti súboru roztokov homogénneho systému. Uvažujme teraz o homogénnom systéme m lineárnych rovníc s n neznámych (3.7), za predpokladu, ako je uvedené vyššie, že matica (3.2) má hodnosť rovnajúcu sa r a že základná minoritná М sa nachádza v ľavom hornom rohu tejto matice. Pretože tentokrát sú všetky b i rovné nule, namiesto vzorcov (3.20) dostaneme nasledujúce vzorce:
vyjadrenie hodnôt neznámych x j = c j (j = 1, 2, ..., r) z hľadiska koeficientov neznámych a ľubovoľne daných hodnôt c r + 1, ..., c n. Na základe toho, čo bolo preukázané v predchádzajúcom odseku vzorce (3.24) obsahujú akékoľvek riešenie homogénneho systému (3.7).
Teraz overme, či je zbierka všetkých riešení homogénneho systému (3.7) tvorí lineárny priestor.
Nech X 1 = (x (1) 1, x (1) 2, ..., x (1) n) a X 2 = (x (2) 1, x (2) 2, ..., x ( 2) n) sú dve ľubovoľné riešenia homogénneho systému (3.7) a λ je akékoľvek skutočné číslo. Pretože každé riešenie homogénnej sústavy (3.7) je prvkom lineárneho priestoru А n všetkých usporiadaných zbierok n čísel, stačí dokázať, že každá z týchto dvoch zbierok
X 1 + X 2 = (x (1) 1 + x (2) 1, ..., x (1) n + x (2) n)
λ X 1 = (λ x (1) 1, ..., λ x (1) n)
je tiež riešením homogénneho systému (3.7).
Uvažujme napríklad o akejkoľvek rovnici systému (3.7) i-ta rovnica, a v tejto rovnici dosadiť namiesto neznámych prvkov uvedených množín. Ak vezmeme do úvahy, že X 1 a X 2 sú riešenia homogénneho systému, budeme mať
a to znamená, že zbierky X 1 + X 2 a λ X 1 sú roztokmi homogénneho systému (3.7).
Súbor všetkých riešení homogénneho systému (3.7) teda tvorí lineárny priestor, ktorý označujeme R.
Nájdeme rozmer tohto priestoru R a zostrojíme v ňom základ.
Dokážme, že za predpokladu, že hodnosť matice homogénneho systému (3.7) sa rovná r, lineárny priestor R všetkých riešení homogénnej sústavy (3.7) je izomorfný s lineárnym priestorom A n-r všetkých usporiadaných zbierok (n- r) čísel(n priestor A m bol zavedený v príklade 3, oddiele 1, oddiele 1, kapitole 2).
Každé riešenie (c 1, ..., c r, c r + 1, ..., c n) homogénneho systému (3.7) priradíme k prvku (c r + 1, ..., c n) priestoru ALE n-r Pretože čísla c r + 1, ..., c n je možné zvoliť ľubovoľne a pre každú voľbu pomocou vzorcov (3.24) jednoznačne určiť riešenie systému (3.7), korešpondencia, ktorú sme stanovili, je jeden na jedného... Ďalej si všimnite, že ak prvky c (1) r + 1, ..., c (1) n a c (2) r + 1, ..., c (2) n priestoru ALE n-r zodpovedajú prvkom (c (1) 1, ..., c (1) r, c (1) r + 1, ..., c (1) n) a (c (2) 1, ... , c (2) r, c (2) r + 1, ..., c (2) n) priestoru R, potom zo vzorcov (3.24) bezprostredne vyplýva, že prvok (c (1) r + 1 + c) (2) r + 1, ..., c (1) n + c (2) n) zodpovedá prvku (c (1) 1 + c (2) 1, ..., c (1) r + c (2) r, c (1) r + 1 + c (2) r + 1, ..., c (1) n + c (2) n) a prvok (λ c (1) r + 1, ..., λ c (1) n) pre akékoľvek reálne λ tam zodpovedá prvku (λ c (1) 1, ..., λ c (1) r, λ c (1) r + 1,. .., λ c (1) n). To dokazuje, že korešpondencia, ktorú sme vytvorili, je izomorfizmus.
Lineárny priestor R všetkých riešení homogénneho systému (3.7) s n neznámym a hodnosťou hlavnej matice rovnajúcou sa r je teda izomorfný s priestorom ALE n-r a preto má rozmer n - r.
Akákoľvek zbierka (n - r) lineárne nezávislých riešení homogénneho systému (3.7) tvorí (podľa vety 2.5) základ v priestore R všetkých riešení a nazýva sa základný súbor riešení homogénneho systému (3.7).
Ak chcete vybudovať základnú sadu riešení, môžete ísť z akéhokoľvek priestoru ALE n-r... Súbor riešení systému (3.7) zodpovedajúci tomuto základu bude v dôsledku izomorfizmu lineárne nezávislý, a preto bude zásadným súborom riešení.
Zvlášť sa rozlišuje základný súbor riešení systému (3.7), ktorý zodpovedá najjednoduchšiemu základu e 1 = (1, 0, 0, ..., 0), e 2 = (1, 1, 0, ..., 0), ..., е nr = (0, 0, 0, ..., 1) priestoru ALE n-r a nazval normálny základný súbor riešení homogénneho systému (3.7).
Podľa vyššie uvedených predpokladov o hodnosti a umiestnení základného molálu má podľa vzorcov (3.24) normálny základný súbor riešení homogénneho systému (3.7) tvar:
Podľa definície základu môže byť vo forme reprezentované akékoľvek riešenie X homogénneho systému (3.7)
X = C 1 X 1 + C 2 X 2 + ... + C n-r X n-r, (3,26)
kde C 1, C 2, ..., C n-r sú niektoré konštanty. Pretože vzorec (3.26) obsahuje akýkoľvek roztok homogénneho systému (3.7), poskytuje tento vzorec všeobecné riešenie uvažovaného homogénneho systému.
Príklad. Zvážte homogénny systém rovníc:
zodpovedajúce nehomogénnemu systému (3.21) analyzovanému v príklade na konci predchádzajúcej časti. Tam sme zistili, že hodnosť r matice tohto systému sa rovná dvom, a ako základ sme použili minor v ľavom hornom rohu indikovanej matice.
Opakovaním úvah na konci predchádzajúcej časti získame namiesto vzorcov (3.22) vzťahy
c 1 = - 3/2 c 3 - c 4, c 2 = - 1/2 c 3 - 2c 4,
platí pre ľubovoľne zvolené c 3 a c 4. Pomocou týchto vzťahov (za predpokladu, že najskôr c 3 = 1, c 4 = 0 a potom c 3 = 0, c 4 = 1) získame normálnu základnú množinu dvoch riešení systému (3.27):
X 1 = (-3 / 2, -1 / 2,1,0), X2 = (-1, -2, 0,1). (3,28)
kde C1 a C2 sú ľubovoľné konštanty.
Na záver tohto podsekcie nadväzujeme spojenie medzi riešeniami nehomogénneho lineárneho systému (3.1) a zodpovedajúceho homogénneho systému (3.7) (s rovnakými koeficientmi pre neznáme). Dokážme nasledujúce dve tvrdenia.
1 °. Súčet akéhokoľvek riešenia nehomogénneho systému (3.1) s akýmkoľvek riešením zodpovedajúceho homogénneho systému (3.7) je riešením systému (3.1).
Skutočne, ak c 1, ..., cn je riešenie systému (3.1), ad 1, ..., dn je riešením zodpovedajúceho homogénneho systému (3.7), potom nahradením v ľubovoľnom (napríklad v i) rovnicu systému (3.1) namiesto neznámych čísel c 1 + d 1, ..., cn + dn, získame
Q.E.D.
2 °. Rozdiel dvoch ľubovoľných riešení nehomogénneho systému (3.1) je riešením zodpovedajúceho homogénneho systému (3.7).
Skutočne, ak c "1, ..., c" n a c "1, ..., c" n sú dve ľubovoľné riešenia systému (3.1), potom nahradením v akejkoľvek (napríklad v i) rovnici sústavy (3.7) namiesto neznámych čísel c "1 - c" 1, ..., c "n - c" n, získame
Q.E.D.
Z preukázaných tvrdení vyplýva, že, nájdením jedného riešenia nehomogénneho systému (3.1) a jeho pridaním do každého riešenia zodpovedajúceho homogénneho systému (3.7) získame všetky riešenia nehomogénneho systému (3.1).
Inými slovami, súčet konkrétneho riešenia nehomogénneho systému (3.1) a všeobecného riešenia zodpovedajúceho homogénneho systému (3.7) dáva všeobecné riešenie nehomogénneho systému (3.1).
Ako konkrétne riešenie nehomogénneho systému (3.1) je prirodzené brať jeho riešenie (v tomto prípade sa predpokladá, ako je uvedené vyššie, že rady hlavných a rozšírených matíc systému (3.1) sa rovnajú r a že základná moll je v ľavom hornom rohu týchto matíc)
ktoré sa získa, ak sú všetky čísla c r + 1, ..., c n vo vzorcoch (3.20) nastavené na rovné nule. Sčítaním tohto konkrétneho riešenia so všeobecným riešením (3.26) zodpovedajúceho homogénneho systému získame nasledujúci výraz pre všeobecné riešenie nehomogénneho systému (3.1):
X = X 0 + C 1 X 1 + C 2 X 2 + ... + C n-r X n-r. (3,30)
V tomto vyjadrení X 0 označuje konkrétne riešenie (3,29), C1, C2, ..., Cnr sú ľubovoľné konštanty a X1, X2, ..., X nr sú prvky normálnej základnej množiny roztokov (3.25) zodpovedajúci homogénny systém.
Takže pre nehomogénny systém (3.21) uvažovaný na konci predchádzajúcej časti sa konkrétne riešenie formy (3.29) rovná X 0 = (6,2,0,0).
Sčítaním tohto konkrétneho roztoku so všeobecným riešením (3.28) zodpovedajúceho homogénneho systému (3.27) získame nasledujúce všeobecné riešenie nehomogénneho systému (3.21):
X = (6,2,0,0) + C1 (-3 / 2, -1 / 2,1,0) + C2 (-1, -2, 0,1). (3,31)
Tu sú C1 a C2 ľubovoľné konštanty.
4. Záverečné poznámky k riešeniu lineárnych systémov. Metódy riešenia lineárnych systémov vyvinuté v predchádzajúcich odsekoch
naraziť na potrebu vypočítať hodnosť matice a nájsť jej základnú menšiu hodnotu. Potom, čo sa nájde bázový mol, sa riešenie zredukuje na techniku výpočtu determinantov a na použitie Cramerových vzorcov.
Na výpočet poradia matice môžete použiť nasledujúce pravidlo: pri výpočte hodnosti matice by sme mali prejsť z mladistvých nižších rádov na mladistvých vyšších rádov; navyše, ak už bol nájdený nenulový mol M rádu k, potom hraničia iba s maloletými rádu (k + 1)(to znamená, že obsahuje menšie M) tento menší je M; ak sú všetky hraničné neplnoleté rády (k + 1) rovné nule, hodnosť matice sa rovná k(v skutočnosti v tomto prípade všetky riadky (stĺpce) matice patria k lineárnemu trupu jeho k radov (stĺpcov), v priesečníku ktorých je menšie M a rozmer uvedeného lineárneho trupu je rovnaký až k).
Uveďme ďalšie pravidlo pre výpočet hodnosti matice. Všimnite si toho, že s riadkami (stĺpcami) matice je možné vytvárať tri základné operácie ktoré nemenia poradie tejto matice: 1) permutácia dvoch riadkov (alebo dvoch stĺpcov), 2) násobenie riadka (alebo stĺpca) akýmkoľvek nenulovým faktorom, 3) pridanie ľubovoľnej lineárnej kombinácie do jedného riadka (stĺpca) ostatných riadkov (stĺpcov) (tieto tri operácie nemenia poradie matice, pretože operácie 1) a 2) nemenia maximálny počet lineárne nezávislých riadkov (stĺpcov) matice a operácie 3) má tú vlastnosť, že lineárny trup všetkých riadkov (stĺpcov) dostupných pred touto operáciou sa zhoduje s lineárnou obálkou všetkých riadkov (stĺpcov) získaných po tejto operácii).
Hovoríme, že matica || a ij || obsahujúca m riadkov a n stĺpcov má uhlopriečka formu, ak sú všetky jej prvky rovné nule, iné ako a 11, a 22, .., a rr, kde r = min (m, n). Poradie takejto matice je očividne r.
Postarajme sa o to pomocou troch elementárnych operácií akákoľvek matica
môže byť zmenšený na diagonálny tvar(čo nám umožňuje vypočítať jeho hodnosť).
Skutočne, ak sú všetky prvky matice (3.31) rovné nule, potom bola táto matica už redukovaná na diagonálny tvar. Ak mat-
Ak matica (3.31) obsahuje nenulové prvky, potom permutáciou dvoch riadkov a dvoch stĺpcov je možné dosiahnuť, aby prvok a 11 bol nenulový. Potom, vynásobením prvého riadka matice číslom 11 -1, zmeníme prvok a 11 na jeden. Ďalej odčítajte zo stĺpca j-ro matice (pre j = 2, 3, ..., n) prvý stĺpec vynásobený a i1 a potom odčítajte z i-tého riadka (pre i = 2, 3 , ..., n) prvý riadok vynásobený a i1 dostaneme namiesto (3.31) maticu nasledujúceho tvaru:
Vykonaním operácií, ktoré sme už popísali, s maticou, odobratou v rámci a pokračovaním v podobnom spôsobe, po konečnom počte krokov, získame maticu diagonálneho tvaru.
Metódy riešenia lineárnych systémov popísané v predchádzajúcich odsekoch, ktoré v konečnom dôsledku používajú aparát Cramerových vzorcov, môžu viesť k veľkým chybám v prípade, keď sú hodnoty koeficientov rovníc a voľných výrazov uvedené približne alebo keď sú tieto hodnoty Sa počas výpočtov zaokrúhľujú.
Toto sa primárne týka prípadu, keď je matica zodpovedajúca hlavnému determinantu (alebo zásadnej minorite) zle podmienené(tj. keď „malé“ zmeny v prvkoch tejto matice zodpovedajú „veľkým“ zmenám v prvkoch inverznej matice). Prirodzene, v tomto prípade bude riešenie lineárneho systému nestabilný(tj „veľké“ zmeny v riešení budú zodpovedať „malým“ zmenám v hodnotách koeficientov rovníc a voľných výrazov).
Tieto okolnosti vedú k potrebe vyvinúť ďalšie (odlišné od Cramerových vzorcov) teoretické algoritmy na nájdenie riešenia a numerické metódy na riešenie lineárnych systémov.
V časti 4 kapitole 4 sa zoznámime s metódou regularizácie A.N. Tichonov nájdenie tzv normálne(t.j. najbližšie k pôvodu) riešenie lineárnej sústavy.
Kapitola 6 poskytne základné informácie o tzv iteračné metódy riešenia lineárnych systémov, ktoré umožňujú riešenie týchto systémov pomocou postupných aproximácií neznámych.
Systém m lineárnych rovníc s n neznámym nazývaný systém formulára
kde a ij a b i (i=1,…,m; b=1,…,n) Sú niektoré známe čísla a x 1, ..., x n- neznámy. Pri označení koeficientov a ij prvý index i označuje číslo rovnice a druhé j- počet neznámych, na ktorých tento koeficient stojí.
Koeficienty pre neznáme napíšeme vo forme matice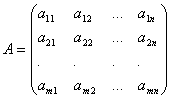 
, ktorý zavoláme systémová matica.
Čísla na pravých stranách rovníc b 1, ..., b m sa volajú voľní členovia.
Agregát nčísla c 1, ..., c n zavolal rozhodnutie daného systému, ak sa každá rovnica systému zmení na rovnosť po substitúcii čísel do nej c 1, ..., c n namiesto zodpovedajúcich neznámych x 1, ..., x n.
Našou úlohou bude nájsť riešenia systému. V takom prípade môžu nastať tri situácie:
Nazýva sa sústava lineárnych rovníc, ktorá má aspoň jedno riešenie kĺb... V opačnom prípade, t.j. ak systém nemá žiadne riešenia, potom sa nazýva nekonzistentné.
Zvážte spôsoby, ako nájsť riešenia systému.
METÓDA MATRIXU NA RIEŠENIE SYSTÉMOV LINEÁRNYCH ROVNOVÁH
Matice umožňujú stručne zapísať sústavu lineárnych rovníc. Nech je daný systém 3 rovníc s tromi neznámymi:
Zoberme si maticu systému 
a maticové stĺpce neznámych a voľných výrazov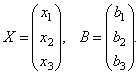 
Poďme si nájsť prácu
tí. ako výsledok súčinu dostaneme ľavé strany rovníc tohto systému. Potom pomocou definície rovnosti matíc možno tento systém napísať vo forme
alebo kratšie A∙X = B.
Tu matice A a B sú známe a matica X neznáme. Tiež ju treba nájsť, tk. jeho prvky sú riešením tohto systému. Táto rovnica sa nazýva maticová rovnica.
Nech je determinant matice nenulový | A| ≠ 0. Potom sa maticová rovnica vyrieši nasledovne. Obe strany rovnice vľavo vynásobíme maticou A -1, inverzná matica A:. Pretože A -1 A = E a E∙X = X, potom získame riešenie maticovej rovnice vo forme X = A -1 B .
Všimnite si toho, že pretože inverznú maticu možno nájsť iba pre štvorcové matice, maticová metóda môže vyriešiť iba tie systémy, v ktorých počet rovníc sa zhoduje s počtom neznámych... Maticová reprezentácia systému je však možná aj v prípade, keď sa počet rovníc nerovná počtu neznámych, potom matica A nebude hranatá, a preto nie je možné nájsť riešenie systému vo forme X = A -1 B.
Príklady Riešenie sústav rovníc.
PRAVIDLO KRAMERY
Uvažujme o systéme troch lineárnych rovníc s tromi neznámymi:
Determinant tretieho rádu zodpovedajúci matici systému, t.j. zložený z koeficientov s neznámymi,
zavolal determinant systému.
Zostavme ďalšie tri determinanty takto: nahraďte v determinante D postupne 1, 2 a 3 stĺpce stĺpcom voľných členov
Potom je možné dokázať nasledujúci výsledok.
Veta (Cramerovo pravidlo). Ak je determinantom systému Δ ≠ 0, potom uvažovaný systém má jedno a iba jedno riešenie a
Dôkaz... Uvažujme teda o systéme 3 rovníc s tromi neznámymi. Vynásobme 1. rovnicu systému algebraickým doplnkom A 11 element a 11, 2. rovnica - zapnuté A 21 a 3. - ďalej A 31:
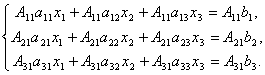
Pridajme tieto rovnice:
Pozrime sa na každú zátvorku a pravú stranu tejto rovnice. Podľa vety o rozšírení determinantu z hľadiska prvkov 1. stĺpca
Podobne sa dá ukázať, že a.
Nakoniec je to ľahké vidieť 
Získame tak rovnosť :.
V dôsledku toho.
Rovnosti a sú odvodené podobným spôsobom, odkiaľ nasleduje tvrdenie vety.
Poznamenávame teda, že ak je determinantom systému Δ ≠ 0, potom má systém jedinečné riešenie a naopak. Ak je determinant systému rovný nule, potom má systém buď nekonečnú množinu riešení, alebo nemá žiadne riešenia, t.j. nekonzistentné.
Príklady Riešiť sústavu rovníc
METÓDA GAUSOV
Predtým uvažované metódy je možné použiť iba na riešenie tých systémov, v ktorých sa počet rovníc zhoduje s počtom neznámych a determinant systému musí byť nenulový. Gaussova metóda je univerzálnejšia a vhodná pre systémy s ľubovoľným počtom rovníc. Spočíva v postupnom odstraňovaní neznámych z rovníc systému.
Uvažujme opäť o systéme troch rovníc s tromi neznámymi:
.
Prvú rovnicu ponecháme nezmenenú a z druhej a tretej vylúčime výrazy obsahujúce x 1... Na to rozdelíme druhú rovnicu ale 21 a vynásobte - ale 11 a potom ho pridajte do 1. rovnice. Podobne rozdelíme tretiu rovnicu na ale 31 a vynásobte - ale 11, a potom pridajte k prvému. V dôsledku toho bude mať pôvodný systém formu:
Teraz z poslednej rovnice vylúčime termín obsahujúci x 2... Za týmto účelom rozdeľte tretiu rovnicu o, vynásobte a pridajte k druhej. Potom budeme mať systém rovníc:
Preto je z poslednej rovnice ľahké nájsť x 3, potom z 2. rovnice x 2 a nakoniec od 1. - x 1.
Pri použití Gaussovej metódy je možné rovnice podľa potreby prehodiť.
Namiesto písania nového systému rovníc sa často obmedzujú na zápis rozšírenej matice systému:
a potom ho pomocou elementárnych transformácií priveďte do trojuholníkového alebo diagonálneho tvaru.
TO elementárne transformácie matice obsahujú nasledujúce transformácie:
- preskupenie riadkov alebo stĺpcov;
- vynásobenie reťazca nenulovým číslom;
- pridanie ďalších riadkov do jedného riadku.
Príklady: Riešenie sústav rovníc Gaussovou metódou.
Systém má teda nekonečné množstvo riešení.
Preskúmať kompatibilitu systému lineárnych agebraických rovníc (SLAE) znamená zistiť, či tento systém má riešenia alebo nie. Ak existujú riešenia, uveďte, koľko z nich.
Potrebujeme informácie z témy "Systém lineárnych algebraických rovníc. Základné pojmy. Maticový zápis". Potrebné sú najmä také pojmy, ako sú matica systému a rozšírená matica systému, pretože práve na nich je založená formulácia Kroneckerovej-Capelliho vety. Ako obvykle, matica systému bude označená písmenom $ A $ a rozšírená matica systému písmenom $ \ widetilde (A) $.
Kroneckerova-Capelliho veta
Systém lineárnych algebraických rovníc je konzistentný vtedy a len vtedy, ak sa hodnosť matice systému rovná hodnosti rozšírenej matice systému, t.j. $ \ rang A = \ rang \ widetilde (A) $.
Pripomeniem, že systém sa nazýva kĺbový, ak má aspoň jedno riešenie. Kroneckerova-Capelliho veta hovorí nasledovné: ak $ \ rang A = \ rang \ widetilde (A) $, potom existuje riešenie; ak $ \ rang A \ neq \ rang \ widetilde (A) $, potom tento SLAE nemá žiadne riešenia (nekonzistentné). Odpoveď na otázku o počte týchto riešení je daná dôsledkom Kroneckerovej-Capelliho vety. Pri formulácii dôsledku sa používa písmeno $ n $, ktoré sa rovná počtu premenných daného SLAE.
Dôsledok z Kroneckerovej-Capelliho vety
- Ak $ \ rang A \ neq \ rang \ widetilde (A) $, potom je SLAE nekonzistentný (nemá žiadne riešenia).
- Ak $ \ rang A = \ rang \ widetilde (A)< n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
- Ak $ \ rang A = \ rang \ widetilde (A) = n $, potom je SLAE definitívne (má presne jedno riešenie).
Všimnite si toho, že vyššie uvedená veta a jej dôsledky neindikujú, ako nájsť riešenie SLAE. S ich pomocou môžete zistiť iba to, či tieto riešenia existujú alebo nie, a ak existujú, potom koľko.
Príklad č. 1
Preskúmajte SLAE $ \ left \ (\ begin (zarovnané) & -3x_1 + 9x_2-7x_3 = 17; \\ & -x_1 + 2x_2-4x_3 = 9; \\ & 4x_1-2x_2 + 19x_3 = -42. \ End (zarovnané ) \ right. $ za kompatibilitu Ak je SLAE kompatibilný, uveďte počet riešení.
Na zistenie existencie riešení pre danú SLAE používame Kroneckerovu-Capelliho vetu. Potrebujeme maticu systému $ A $ a rozšírenú maticu systému $ \ widetilde (A) $, zapíšeme ich:
$$ A = \ left (\ begin (array) (ccc) -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \ end (array) \ right); \; \ widetilde (A) = \ left (\ begin (array) (ccc | c) -3 & 9 & -7 & 17 \\ -1 & 2 & -4 & 9 \\ 4 & -2 & 19 & -42 \ end (pole) \ vpravo). $$
Nájdite $ \ rang A $ a $ \ rang \ widetilde (A) $. Existuje mnoho spôsobov, ako to urobiť, niektoré z nich sú uvedené v sekcii Hodnotenie matice. Na štúdium takýchto systémov sa spravidla používajú dve metódy: „Výpočet poradia matice podľa definície“ alebo „Výpočet hodnosti matice metódou elementárnych transformácií“.
Metóda číslo 1. Výpočet hodností podľa definície.
Podľa definície je poradie najvyšším poradím neplnoletých matíc, medzi ktorými je najmenej jedno nenulové číslo. Štúdia zvyčajne začína s mladistvými prvého rádu, ale tu je pohodlnejšie začať okamžite počítať moll tretieho rádu matice $ A $. Prvky minor menšieho rádu sú na priesečníku troch riadkov a troch stĺpcov uvažovanej matice. Pretože matica $ A $ obsahuje iba 3 riadky a 3 stĺpce, molár tretieho rádu matice $ A $ je determinantom matice $ A $, t.j. $ \ Delta A $. Na výpočet determinantu použijeme vzorec č. 2 z témy „Vzorce na výpočet determinantov druhého a tretieho rádu“:
$$ \ Delta A = \ vľavo | \ begin (array) (ccc) -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \ end (array) \ right | = -21. $$
Existuje teda molár tretieho rádu matice $ A $, ktorý sa nerovná nule. Nie je možné zostaviť menšiu časť štvrtého rádu, pretože vyžaduje 4 riadky a 4 stĺpce a v matici $ A $ sú iba 3 riadky a 3 stĺpce. Takže najvyššie poradie neplnoletých matice $ A $, medzi ktorými je aspoň jedna nenulová, sa rovná 3. Preto $ \ rang A = 3 $.
Musíme tiež nájsť $ \ rang \ widetilde (A) $. Pozrime sa na štruktúru matice $ \ widetilde (A) $. Matica $ \ widetilde (A) $ obsahuje prvky matice $ A $ a zistili sme, že $ \ Delta A \ neq 0 $. Preto matica $ \ widetilde (A) $ má moll tretieho rádu, ktorý nie je nulový. Nemôžeme poskladať neplnoleté osoby štvrtého rádu z matice $ \ widetilde (A) $, preto usudzujeme: $ \ rang \ widetilde (A) = 3 $.
Keďže $ \ rang A = \ rang \ widetilde (A) $, podľa Kroneckerovej-Capelliho vety je systém konzistentný, t.j. má riešenie (aspoň jedno). Aby sme uviedli počet riešení, vezmime do úvahy, že náš SLAE obsahuje 3 neznáme: $ x_1 $, $ x_2 $ a $ x_3 $. Pretože počet neznámych je $ n = 3 $, usudzujeme: $ \ rang A = \ rang \ widetilde (A) = n $, preto podľa dôsledkov z Kroneckerovej-Capelliho vety je systém určitý, t.j. má len jedno riešenie.
Problém je vyriešený. Aké sú nevýhody a výhody tejto metódy? Najprv si povedzme niečo o profesionáloch. Najprv sme museli nájsť iba jeden determinant. Potom sme okamžite urobili záver o počte riešení. V štandardných štandardných výpočtoch sú zvyčajne uvedené systémy rovníc, ktoré obsahujú tri neznáme a majú jedinečné riešenie. Pre takéto systémy táto metóda je to veľmi výhodné, pretože vopred vieme, že existuje riešenie (inak by pri typickom výpočte nebol žiadny príklad). Títo. musíme len ukázať existenciu riešenia väčšiny rýchly spôsob... Za druhé, vypočítaná hodnota determinantu matice systému (t.j. $ \ Delta A $) bude užitočná po: keď začneme daný systém riešiť Cramerovou metódou alebo pomocou inverznej matice.
Metóda výpočtu poradia je však z definície nežiaduca, ak je matica systému $ A $ obdĺžniková. V tomto prípade je lepšie použiť druhú metódu, ktorá bude diskutovaná nižšie. Navyše, ak $ \ Delta A = 0 $, potom nemôžeme povedať nič o počte riešení danej nehomogénnej SLAE. Možno má SLAE nekonečný počet riešení, alebo možno žiadne. Ak je $ \ Delta A = 0 $, je potrebný ďalší výskum, ktorý je často ťažkopádny.
Zhrnutím toho, čo bolo povedané, poznamenávam, že prvá metóda je dobrá pre tie SLAE, v ktorých je matica systému štvorcová. V tomto prípade samotný SLAE obsahuje tri alebo štyri neznáme a je prevzatý zo štandardných typických výpočtov alebo kontrolných prác.
Metóda číslo 2. Výpočet poradia metódou elementárnych transformácií.
Táto metóda je podrobne popísaná v súvisiacej téme. Vypočítame hodnosť matice $ \ widetilde (A) $. Prečo práve matice $ \ widetilde (A) $ a nie $ A $? Faktom je, že matica $ A $ je súčasťou matice $ \ widetilde (A) $, a preto pri výpočte hodnosti matice $ \ widetilde (A) $ súčasne nájdeme hodnosť matice $ A $.
\ begin (zarovnané) & \ widetilde (A) = \ left (\ begin (pole) (ccc | c) -3 & 9 & -7 & 17 \\ -1 & 2 & -4 & 9 \\ 4 & - 2 & 19 & -42 \ end (pole) \ right) \ rightarrow \ left | \ text (swap first and second lines) \ right | \ rightarrow \\ & \ rightarrow \ left (\ begin (array) (ccc | c) -1 & 2 & -4 & 9 \\ -3 & 9 & -7 & 17 \\ 4 & -2 & 19 & - 42 \ end (pole) \ right) \ begin (pole) (l) \ phantom (0) \\ r_2-3r_1 \\ r_3 + 4r_1 \ end (array) \ rightarrow \ left (\ begin (array) (ccc | c) -1 & 2 & -4 & 9 \\ 0 & 3 & 5 & -10 \\ 0 & 6 & 3 & -6 \ end (array) \ right) \ begin (array) (l) \ phantom ( 0) \\ \ phantom (0) \\ r_3-2r_2 \ end (array) \ rightarrow \\ & \ rightarrow \ left (\ begin (array) (ccc | c) -1 & 2 & -4 & 9 \\ 0 & 3 & 5 & -10 \\ 0 & 0 & -7 & 14 \ end (pole) \ right) \ end (zarovnané)
Maticu $ \ widetilde (A) $ sme transformovali do stupňovitej podoby. Výsledná kroková matica má tri nenulové riadky, takže jej poradie je 3. V dôsledku toho je hodnosť matice $ \ widetilde (A) $ 3, to znamená, $ \ rang \ widetilde (A) = 3 $. Pri transformácii s prvkami matice $ \ widetilde (A) $ sme súčasne transformovali prvky matice $ A $, umiestnené až po čiaru. Matica $ A $ je tiež odstupňovaná: $ \ left (\ begin (array) (ccc) -1 & 2 & -4 \\ 0 & 3 & 5 \\ 0 & 0 & -7 \ end (array) \ right) $. Záver: hodnosť matice $ A $ sa tiež rovná 3, t.j. $ \ zazvonilo A = 3 $.
Keďže $ \ rang A = \ rang \ widetilde (A) $, podľa Kroneckerovej-Capelliho vety je systém konzistentný, t.j. má riešenie. Aby sme uviedli počet riešení, vezmime do úvahy, že náš SLAE obsahuje 3 neznáme: $ x_1 $, $ x_2 $ a $ x_3 $. Pretože počet neznámych je $ n = 3 $, usudzujeme: $ \ rang A = \ rang \ widetilde (A) = n $, preto podľa dôsledkov z Kroneckerovej-Capelliho vety je systém definovaný, t.j. má len jedno riešenie.
Aké sú výhody druhej metódy? Hlavnou výhodou je jeho univerzálnosť. Vôbec nám nezáleží na tom, či je matica systému štvorcová alebo nie. Okrem toho sme skutočne vykonali transformácie dopredného priebehu Gaussovej metódy. Zostáva iba niekoľko akcií a mohli by sme nájsť riešenie tohto SLAE. Ak mám byť úprimný, druhá metóda sa mi páči viac ako prvá, ale výber je vecou vkusu.
Odpoveď: Daný SLAE je konzistentný a definovaný.
Príklad č. 2
Preskúmajte SLAE $ \ left \ (\ begin (zarovnané) & x_1-x_2 + 2x_3 = -1; \\ & -x_1 + 2x_2-3x_3 = 3; \\ & 2x_1-x_2 + 3x_3 = 2; \\ & 3x_1- 2x_2 + 5x_3 = 1; \\ & 2x_1-3x_2 + 5x_3 = -4. \ Koniec (zarovnaný) \ vpravo. $ Z dôvodu kompatibility.
Nájdeme rady matice systému a rozšírenej matice systému metódou elementárnych transformácií. Rozšírená systémová matica: $ \ widetilde (A) = \ left (\ begin (array) (ccc | c) 1 & -1 & 2 & -1 \\ -1 & 2 & -3 & 3 \\ 2 & -1 & 3 & 2 \\ 3 & -2 & 5 & 1 \\ 2 & -3 & 5 & -4 \ end (array) \ right) $. Nájdite požadované poradie transformáciou rozšírenej matice systému:
$$ \ left (\ begin (pole) (ccc | c) 1 & -1 & 2 & -1 \\ -1 & 2 & -3 & 3 \\ 2 & -3 & 5 & -4 \\ 3 & -2 & 5 & 1 \\ 2 & -1 & 3 & 2 \ end (array) \ right) \ begin (array) (l) \ phantom (0) \\ r_2 + r_1 \\ r_3-2r_1 \\ r_4 -3r_1 \\ r_5-2r_1 \ end (pole) \ rightarrow \ left (\ begin (array) (ccc | c) 1 & -1 & 2 & -1 \\ 0 & 1 & -1 & 2 \\ 0 & -1 & 1 & -2 \\ 0 & 1 & -1 & 4 \\ 0 & 1 & -1 & 4 \ end (array) \ right) \ begin (array) (l) \ phantom (0) \\ \ phantom (0) \\ r_3-r_2 \\ r_4-r_2 \\ r_5 + r_2 \ end (array) \ rightarrow \\ $$ $$ \ rightarrow \ left (\ begin (array) (ccc | c) 1 & -1 & 2 & -1 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \ end (pole) \ vpravo) \ begin (pole) (l) \ phantom (0) \\\ phantom (0) \\\ phantom (0) \\ r_4-r_3 \\\ phantom (0) \ end (array) \ rightarrow \ left (\ begin (pole) (ccc | c) 1 & -1 & 2 & -1 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \ end (pole) \ right) $$
Matica rozšíreného systému je stupňovitá. Poradie stupňovitej matice sa rovná počtu jej nenulových riadkov, preto $ \ rang \ widetilde (A) = 3 $. Matica $ A $ (do bodu) sa tiež zredukuje na stupňovitú formu a jej poradie je 2, $ \ rang (A) = 2 $.
Pretože $ \ rang A \ neq \ rang \ widetilde (A) $, podľa Kroneckerovej-Capelliho vety je systém nekonzistentný (t.j. nemá žiadne riešenia).
Odpoveď: Systém je nekonzistentný.
Príklad č. 3
Preskúmajte SLAE $ \ left \ (\ begin (zarovnané) & 2x_1 + 7x_3-5x_4 + 11x_5 = 42; \\ & x_1-2x_2 + 3x_3 + 2x_5 = 17; \\ & -3x_1 + 9x_2-11x_3-7x_5 = -64 ; \\ & -5x_1 + 17x_2-16x_3-5x_4-4x_5 = -90; \\ & 7x_1-17x_2 + 23x_3 + 15x_5 = 132. \ Koniec (zarovnaný) \ vpravo. $ Z dôvodu kompatibility.
Rozšírenú maticu systému uvedieme do postupnej podoby:
$$ \ left (\ begin (array) (ccccc | c) 2 & 0 & 7 & -5 & 11 & 42 \\ 1 & -2 & 3 & 0 & 2 & 17 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \ end (array) \ right) \ overset (r_1 \ leftrightarrow (r_3)) (\ rightarrow) $$ $$ \ rightarrow \ left (\ begin (array) (ccccc | c) 1 & -2 & 3 & 0 & 2 & 17 \\ 2 & 0 & 7 & -5 & 11 & 42 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \ end (pole) \ right) \ begin (pole) (l) \ phantom (0) \\ r_2-2r_1 \\ r_3 + 3r_1 \\ r_4 + 5r_1 \\ r_5-7r_1 \ end ( pole) \ rightarrow \ left (\ begin (array) (ccccc | c) 1 & -2 & 3 & 0 & 2 & 17 \\ 0 & 4 & 1 & -5 & 7 & 8 \\ 0 & 3 & - 2 & 0 & -1 & -13 \\ 0 & 7 & -1 & -5 & 6 & -5 \\ 0 & -3 & 2 & 0 & 1 & 13 \ end (array) \ right) \ begin ( pole) (l) \ phantom (0) \\ \ phantom (0) \\ 4r_3 + 3r_2 \\ 4r_4-7r_2 \\ 4r_5 + 3r_2 \ end (array) \ rightarrow $$ \ rightarrow \ left (\ begin (array ) (ccccc | c) 1 & -2 & 3 & 0 & 2 & 17 \\ 0 & 4 & 1 & -5 & 7 & 8 \\ 0 & 0 & -11 & 15 & -25 & -76 \\ 0 & 0 & -11 & 15 & -25 & -76 \\ 0 & 0 & 11 & -15 & 25 & 76 \ end (array) \ right) \ begin (array) (l) \ phantom (0) \\ \ phantom (0) \\\ phantom (0) \\ r_4 -r_3 \\ r_5 + r_2 \ end (pole) \ rightarrow \ left (\ begin (array) (ccccc | c) 1 & -2 & 3 & 0 & 2 & 17 \\ 0 & 4 & 1 & -5 & 7 & 8 \\ 0 & 0 & -11 & 15 & -25 & -76 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \ end (pole) \ vpravo) $$
Rozšírenú systémovú maticu a samotnú systémovú maticu sme priviedli do stupňovitej podoby. Poradie rozšírenej matice systému je tri, hodnosť matice systému je tiež tri. Keďže systém obsahuje $ n = 5 $ neznámych, t.j. $ \ rang \ widetilde (A) = \ rang (A) \ lt (n) $, potom podľa dôsledkov na Kroneckerovu-Capelliho vetu tento systém nie je definovaný, t.j. má nekonečné množstvo riešení.
Odpoveď: systém je nedefinovaný.
V druhej časti analyzujeme príklady, ktoré sú často zahrnuté v typických výpočtoch alebo testoch z vyššej matematiky: štúdiu kompatibility a riešenie SLAE v závislosti od hodnôt v nej zahrnutých parametrov.
Príklad 1... Nájdite všeobecné riešenie a konkrétne riešenie systémuRiešenie vykonávame pomocou kalkulačky. Vypíšeme rozšírené a základné matice: 
Prerušovaná čiara oddeľuje hlavnú maticu A. Hore píšeme neznáme systémy, majúc na pamäti možné preskupenie výrazov v rovniciach systému. Pri určovaní poradia rozšírenej matice súčasne nájdeme poradie a hlavnú. V matici B sú prvý a druhý stĺpec proporcionálne. Z dvoch proporcionálnych stĺpcov môže do základného molálu spadnúť iba jeden, preto prenesieme napríklad prvý stĺpček za prerušovanú čiaru s opačným znamienkom. Pre systém to znamená presunutie výrazov z x 1 na pravú stranu rovníc. 
Prenesme maticu do trojuholníkového tvaru. Budeme pracovať iba s riadkami, pretože vynásobenie riadka matice číslom iným ako nula a pridanie do ďalšieho riadka pre systém znamená vynásobenie rovnice rovnakým číslom a jej sčítanie s ďalšou rovnicou, čo nemení riešenie systém. Pracujeme s prvým riadkom: vynásobte prvý riadok matice (-3) a postupne pridajte do druhého a tretieho radu. Potom vynásobíme prvý riadok (-2) a pridáme do štvrtého. 
Druhý a tretí riadok sú proporcionálne, preto jeden z nich, napríklad druhý, môže byť prečiarknutý. To sa rovná vymazaniu druhej rovnice systému, pretože je to dôsledok tretej. 
Teraz pracujeme s druhým riadkom: vynásobte ho (-1) a pridajte do tretieho. 
Prerušovaná menšina má najvyššie poradie (z možných neplnoletých) a je nenulová (rovná sa súčinu prvkov na hlavnej uhlopriečke) a táto menšina patrí do hlavnej aj rozšírenej matice, preto rangA = rangB = 3.
Menšia 
je základný. Obsahuje koeficienty pre neznáme x 2, x 3, x 4, čo znamená, že neznáme x 2, x 3, x 4 sú závislé a x 1, x 5 sú voľné.
Transformujeme maticu, pričom vľavo zostane iba báza minor (čo zodpovedá bodu 4 vyššie uvedeného algoritmu riešenia). 
Systém s koeficientmi tejto matice je ekvivalentný pôvodnému systému a má formu
x 4 = 3-4x 5, x 3 = 3-4x 5 -2x 4 = 3-4x 5 -6 + 8x 5 = -3 + 4x 5
x 2 = x 3 + 2x 4 -2 + 2x 1 + 3x 5 = -3 + 4x 5 + 6-8x 5 -2 + 2x 1 + 3x 5 = 1 + 2x 1 -x 5
Dostali sme pomery vyjadrujúce závislé premenné x 2, x 3, x 4 cez voľné x 1 a x 5, to znamená, že sme našli všeobecné riešenie:
Priradením akýchkoľvek hodnôt voľným neznámym získame toľko konkrétnych riešení, koľko sa nám páči. Nájdeme dve konkrétne riešenia:
1) nech x 1 = x 5 = 0, potom x 2 = 1, x 3 = -3, x 4 = 3;
2) zadajte x 1 = 1, x 5 = -1, potom x 2 = 4, x 3 = -7, x 4 = 7.
Našli sme teda dve riešenia: (0,1, -3,3,0) -jedno riešenie, (1,4, -7,7, -1) -ďalšie riešenie.
Príklad 2... Preskúmajte kompatibilitu, nájdite všeobecné a jedno konkrétne riešenie systému 
Riešenie... Prvú a druhú rovnicu preusporiadame tak, aby boli v prvej rovnici jednotné, a napíšeme maticu B. 
V štvrtom stĺpci, ktorý pracuje v prvom riadku, dostaneme nuly: 
Teraz dostaneme nuly v treťom stĺpci pomocou druhého riadka: 
Tretí a štvrtý riadok sú proporcionálne, takže jeden z nich môže byť prečiarknutý bez zmeny poradia:
Tretí riadok vynásobíme (–2) a do štvrtého pridáme: 
Vidíme, že rady hlavných a rozšírených matíc sú rovné 4 a poradie sa zhoduje s počtom neznámych, preto má systém jedinečné riešenie:
-x 1 = -3 → x 1 = 3; x 2 = 3-x 1 → x 2 = 0; x 3 = 1-2x 1 → x 3 = 5.
x 4 = 10 - 3x 1 - 3x 2 - 2x 3 = 11.
Príklad 3... Skontrolujte kompatibilitu systému a nájdite riešenie, ak existuje. 
Riešenie... Zostavujeme rozšírenú maticu systému. 
Prvé dve rovnice preusporiadame tak, aby v ľavom hornom rohu bola 1:
Vynásobením prvého riadka (-1) ho pridajte do tretieho: 
Vynásobte druhý riadok (-2) a pridajte do tretieho: 
Systém je nekonzistentný, pretože v hlavnej matici sme dostali riadok pozostávajúci z núl, ktorý sa pri nájdení poradia prečiarkne, a v rozšírenej matici zostane posledný riadok, to znamená r B> r A.
Úloha... Preskúmajte kompatibilitu tohto systému rovníc a vyriešte ho pomocou maticového počtu.
Riešenie
Príklad... Dokážte kompatibilitu systému lineárnych rovníc a vyriešte ho dvoma spôsobmi: 1) Gaussova metóda; 2) Cramerova metóda. (odpoveď zadajte v tvare: x1, x2, x3)
Riešenie: doc: doc: xls
Odpoveď: 2,-1,3.
Príklad... Je uvedený systém lineárnych rovníc. Dokážte jeho kompatibilitu. Nájdite všeobecné riešenie systému a jedno konkrétne riešenie.
Riešenie
Odpoveď: x 3 = - 1 + x 4 + x 5; x 2 = 1 - x 4; x 1 = 2 + x 4 - 3x 5
Úloha... Nájdite všeobecné a špecifické riešenia pre každý systém.
Riešenie. Preskúmajme tento systém pomocou Kroneckerovej-Capelliho vety.
Vypíšeme rozšírené a základné matice:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Tu je matica A tučne.
Prenesme maticu do trojuholníkového tvaru. Budeme pracovať iba s riadkami, pretože vynásobenie riadka matice číslom iným ako nula a pridanie do ďalšieho riadka pre systém znamená vynásobenie rovnice rovnakým číslom a jej sčítanie s ďalšou rovnicou, čo nemení riešenie systém.
1. riadok vynásobte (3). 2. riadok vynásobte (-1). Pripojme druhý riadok k prvému:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
2. riadok vynásobte (2). Vynásobte 3. riadok (-3). Pridajte tretí riadok do druhého:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
2. riadok vynásobte (-1). Pripojme druhý riadok k prvému:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Zvýraznená minorita má najvyššie poradie (z možných mladistvých) a je nenulová (rovná sa súčinu prvkov na obrátenej uhlopriečke) a táto menšina patrí do hlavnej matice aj do rozšírenej, preto zazvonilo ( A) = zazvonilo (B) = 3. Pretože hodnosť hlavnej matice sa rovná hodnosti rozšírenej, potom systém je kĺbový.
Táto drobnosť je základná. Obsahuje koeficienty pre neznáme x 1, x 2, x 3, čo znamená, že neznáme x 1, x 2, x 3 sú závislé (základné) a x 4, x 5 sú voľné.
Transformujeme maticu, pričom vľavo zostane iba základňa ako menšia.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
27x 3 =
- x 2 + 13x 3 = - 1 + 3x 4 - 6x 5
2x 1 + 3x 2 - 3x 3 = 1 - 3x 4 + 2x 5
Metódou eliminácie neznámych nájdeme:
Získali sme vzťahy vyjadrujúce závislé premenné x 1, x 2, x 3 cez voľné x 4, x 5, to znamená, že sme zistili spoločné rozhodnutie:
x 3 = 0
x 2 = 1 - 3x 4 + 6x 5
x 1 = - 1 + 3x 4 - 8x 5
nedefinované od má viac ako jedno riešenie.
Úloha... Vyriešte sústavu rovníc.
Odpoveď: x 2 = 2 - 1,67 x 3 + 0,67 x 4
x 1 = 5 - 3,67 x 3 + 0,67 x 4
Priradením akýchkoľvek hodnôt voľným neznámym získame toľko konkrétnych riešení, koľko sa nám páči. Systém je nedefinované
