This video tutorial will help users get an idea of the Pyramid theme. Correct pyramid. In this lesson we will get acquainted with the concept of a pyramid, we will give it a definition. Let's consider what a regular pyramid is and what properties it has. Then we prove the theorem on the lateral surface of a regular pyramid.
In this lesson we will get acquainted with the concept of a pyramid, we will give it a definition.
Consider a polygon A 1 A 2...A n, which lies in the plane α, and the point P, which does not lie in the plane α (Fig. 1). Let's connect the point P with peaks A 1, A 2, A 3, … A n... We get n triangles: A 1 A 2 R, A 2 A 3 R etc.
Definition... Polyhedron RA 1 A 2 ... A n composed of n-gonal A 1 A 2...A n and n triangles RA 1 A 2, RA 2 A 3 …PA n А n-1 is called n-gonal pyramid. Rice. 1.
Rice. 1
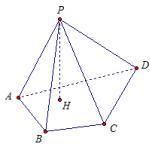
Consider a quadrangular pyramid PABCD(fig. 2).
R- the top of the pyramid.
ABCD- the base of the pyramid.
RA- lateral rib.
AB- the edge of the base.
From point R omit the perpendicular NS on the plane of the base ABCD... The drawn perpendicular is the height of the pyramid.
Rice. 2
The full surface of the pyramid consists of the lateral surface, that is, the area of all lateral faces, and the base area:
S full = S side + S main
A pyramid is called correct if:
- its base is a regular polygon;
- the line segment connecting the top of the pyramid with the center of the base is its height.
Explanation on the example of a regular quadrangular pyramid
Consider a regular quadrangular pyramid PABCD(fig. 3).
R- the top of the pyramid. Base of the pyramid ABCD- a regular quadrangle, that is, a square. Point O, the intersection point of the diagonals, is the center of the square. Means, RO is the height of the pyramid.
Rice. 3
Explanation: in the correct n-gon, the center of the inscribed circle and the center of the circumcircle coincide. This center is called the center of the polygon. It is sometimes said that the top is projected to the center.
The height of the side face of a regular pyramid drawn from its top is called apothem and denoted h a.
1. all lateral edges of a regular pyramid are equal;
2. the side faces are equal isosceles triangles.
The proof of these properties is given by the example of a regular quadrangular pyramid.
Given: PABCD- regular quadrangular pyramid,
ABCD- square,
RO- the height of the pyramid.
Prove:
1. PA = PB = PC = PD
2.∆АВР = ∆ВCP = ∆СDP = ∆DAP See Fig. 4.
Rice. 4
Proof.
RO- the height of the pyramid. That is, straight RO perpendicular to the plane ABC and hence direct AO, VO, SO and DO lying in it. So the triangles ROA, ROV, ROS, POD- rectangular.
Consider a square ABCD... It follows from the properties of the square that AO = BO = CO = DO.
Then right triangles have ROA, ROV, ROS, POD leg RO- general and legs AO, VO, SO and DO are equal, which means that these triangles are equal in two legs. The equality of the triangles implies the equality of the segments, PA = PB = PC = PD. Item 1 is proved.
Segments AB and Sun are equal, since they are sides of one square, PA = PB = RS... So the triangles ABP and HRV - isosceles and equal on three sides.
Similarly, we find that the triangles ATS, BCP, CDP, DAP are isosceles and equal, as required to prove in paragraph 2.
The lateral surface area of a regular pyramid is equal to half the product of the base perimeter times the apothem:
For the proof, we choose a regular triangular pyramid.
Given: RAVS- regular triangular pyramid.
AB = BC = AC.
RO- height.
Prove: 
... See Fig. 5.
Rice. 5
Proof.
RAVS- regular triangular pyramid. That is AB= AC = BC... Let be O- the center of the triangle ABC, then RO is the height of the pyramid. At the base of the pyramid lies an equilateral triangle ABC... notice, that 
.
Triangles RAV, RVS, RSA- equal isosceles triangles (by property). The triangular pyramid has three side faces: RAV, RVS, RSA... This means that the area of the side surface of the pyramid is equal to:
S side = 3S RAV
The theorem is proved.
The radius of a circle inscribed at the base of a regular quadrangular pyramid is 3 m, the height of the pyramid is 4 m. Find the area of the side surface of the pyramid.
Given: regular quadrangular pyramid ABCD,
ABCD- square,
r= 3 m,
RO- the height of the pyramid,
RO= 4 m.
Find: S side. See Fig. 6.
Rice. 6
Solution.
By the proved theorem,.
Let's find the side of the base first AB... We know that the radius of a circle inscribed at the base of a regular quadrangular pyramid is 3 m.
Then, m.
Find the perimeter of the square ABCD with a side of 6 m:
Consider a triangle BCD... Let be M- middle of the side DC... Because O- middle BD, then 
(m).
Triangle DPC- isosceles. M- middle DC... That is, RM- the median, and hence the height in the triangle DPC... Then RM- the apothem of the pyramid.
RO- the height of the pyramid. Then, straight RO perpendicular to the plane ABC, and hence the straight line OM lying in it. Find apothem RM from a right triangle ROM.
Now we can find the side surface of the pyramid:
Answer: 60 m 2.
The radius of a circle circumscribed about the base of a regular triangular pyramid is m. The lateral surface area is 18 m 2. Find the length of the apothem.
Given: ABCP- regular triangular pyramid,
AB = BC = CA,
R= m,
S side = 18 m 2.
Find:. See Fig. 7.
Rice. 7
Solution.
In a regular triangle ABC the radius of the circumscribed circle is given. Let's find a side AB this triangle using the sine theorem.
Knowing the side of a regular triangle (m), we find its perimeter.
By the theorem on the lateral surface area of a regular pyramid, where h a- the apothem of the pyramid. Then:
Answer: 4 m.
So, we examined what a pyramid is, what a regular pyramid is, and proved the theorem on the lateral surface of a regular pyramid. In the next lesson, we will get acquainted with the truncated pyramid.
Bibliography
- Geometry. Grades 10-11: a textbook for students of educational institutions (basic and profile levels) / I. M. Smirnova, V. A. Smirnov. - 5th ed., Rev. and add. - M .: Mnemosina, 2008 .-- 288 p .: ill.
- Geometry. Grade 10-11: Textbook for general educational institutions / Sharygin I.F. - M .: Bustard, 1999. - 208 p.: Ill.
- Geometry. Grade 10: Textbook for educational institutions with in-depth and specialized study of mathematics / E. V. Potoskuev, L. I. Zvalich. - 6th ed., Stereotype. - M .: Bustard, 008 .-- 233 p .: ill.
- Internet portal "Yaklass" ()
- Internet portal "Festival of pedagogical ideas" September 1st "()
- Internet portal "Slideshare.net" ()
Homework
- Can a regular polygon be the base of an irregular pyramid?
- Prove that disjoint edges of a regular pyramid are perpendicular.
- Find the value of the dihedral angle at the side of the base of a regular quadrangular pyramid, if the apothem of the pyramid is equal to the side of its base.
- RAVS- regular triangular pyramid. Construct the linear angle of the dihedral at the base of the pyramid.
Here you can find basic information about the pyramids and related formulas and concepts. All of them are studied with a mathematics tutor in preparation for the exam.
Consider a plane, a polygon 
lying in it and a point S not lying in it. Connect S to all the vertices of the polygon. The resulting polyhedron is called a pyramid. The line segments are called side ribs. The polygon is called the base, and the point S is called the top of the pyramid. Depending on the number n, the pyramid is called triangular (n = 3), quadrangular (n = 4), ptyagonal (n = 5), and so on. An alternative name for the triangular pyramid is tetrahedron... The height of the pyramid is called the perpendicular, lowered from its top to the plane of the base. 
A pyramid is called correct if a regular polygon, and the base of the height of the pyramid (base of the perpendicular) is its center.
Tutor comment:
Do not confuse the concept of "regular pyramid" and "correct tetrahedron". In a regular pyramid, the side edges are not necessarily equal to the edges of the base, but in a regular tetrahedron, all 6 edges of the edges are equal. This is his definition. It is easy to prove that the equality implies the coincidence of the center P of the polygon with the base of the height, so a regular tetrahedron is a regular pyramid.
What is Apothema?
The apothem of a pyramid is the height of its lateral face. If the pyramid is correct, then all its apothems are equal. The converse is not true. 
Tutor in mathematics about his terminology: work with pyramids is 80% built through two types of triangles:
1) Containing apothem SK and height SP
2) Containing a lateral edge SA and its projection PA 
To simplify references to these triangles, it is more convenient for a math tutor to call the first of them apothemic, and second costal... Unfortunately, you will not find this terminology in any of the textbooks, and the teacher has to enter it unilaterally.
The formula for the volume of a pyramid:
1) 
, where is the area of the base of the pyramid, and is the height of the pyramid
2), where is the radius of the inscribed sphere, and is the area of the full surface of the pyramid.
3) 
, where MN is the distance of any two crossing edges, and is the area of the parallelogram formed by the midpoints of the four remaining edges.
Pyramid height base property:
Point P (see figure) coincides with the center of the inscribed circle at the base of the pyramid if one of the following conditions is met:
1) All apothems are equal
2) All side faces are equally inclined towards the base
3) All apothems are equally inclined to the height of the pyramid
4) The height of the pyramid is equally inclined to all side faces
Math Tutor Commentary: Note that all points have one common property: one way or another, side faces are involved everywhere (apothems are their elements). Therefore, the tutor may offer a less accurate, but more convenient for memorization formulation: the point P coincides with the center of the inscribed circle at the base of the pyramid, if there is any equal information about its lateral faces. To prove it, it suffices to show that all apothemic triangles are equal.
Point P coincides with the center of a circle described near the base of the pyramid, if one of three conditions is true:
1) All side edges are equal
2) All side ribs are equally inclined towards the base
3) All side ribs are equally inclined to height
Pyramid Is a polyhedron with one face - the base of the pyramid - an arbitrary polygon, and the rest - side faces - triangles with a common vertex, called the apex of the pyramid. The perpendicular dropped from the top of the pyramid to its base is called pyramid height... A pyramid is called triangular, quadrangular, etc., if the base of the pyramid is a triangle, quadrilateral, etc. A triangular pyramid is a tetrahedron - a tetrahedron. Quadrangular - pentahedron, etc.
Pyramid, Truncated pyramid
Correct pyramid
If the base of the pyramid is a regular polygon, and the height falls to the center of the base, then the pyramid is correct. In a regular pyramid, all side edges are equal, all side edges are equal isosceles triangles. The height of the triangle of the side face of a regular pyramid is called - apothem of the right pyramid.
Truncated pyramid
A section parallel to the base of the pyramid divides the pyramid into two parts. The part of the pyramid between its base and this section is truncated pyramid ... This section for the truncated pyramid is one of its bases. The distance between the bases of the truncated pyramid is called the truncated pyramid height. A truncated pyramid is called correct if the pyramid from which it was obtained was correct. All side faces of a regular truncated pyramid are equal isosceles trapezoids. The height of the trapezoid of the side face of a regular truncated pyramid is called - apothem of the regular truncated pyramid.
Definition. Side edge is a triangle, one corner of which lies at the top of the pyramid, and the opposite side coincides with the side of the base (polygon).
Definition. Side ribs are the common sides of the side faces. The pyramid has as many edges as the corners of the polygon.
Definition. Pyramid height- this is a perpendicular, lowered from the top to the base of the pyramid.
Definition. Apothem is the perpendicular to the side face of the pyramid, lowered from the top of the pyramid to the side of the base.
Definition. Diagonal section is a section of the pyramid by a plane passing through the top of the pyramid and the diagonal of the base.
Definition. Correct pyramid is a pyramid in which the base is a regular polygon, and the height drops to the center of the base.
Volume and surface area of the pyramid
Formula. The volume of the pyramid through the base area and height:
Pyramid properties
If all side edges are equal, then a circle can be described around the base of the pyramid, and the center of the base coincides with the center of the circle. Also, the perpendicular dropped from the top passes through the center of the base (circle).
If all side edges are equal, then they are inclined to the plane of the base at the same angles.
The side edges are equal when they form equal angles with the base plane or if a circle can be described around the base of the pyramid.
If the side faces are inclined to the base plane at one angle, then a circle can be inscribed into the base of the pyramid, and the top of the pyramid is projected into its center.
If the side faces are inclined to the base plane at the same angle, then the apothems of the side faces are equal.
Properties of a regular pyramid
1. The top of the pyramid is equidistant from all corners of the base.
2. All side edges are equal.
3. All side ribs slope at the same angle to the base.
4. The apothems of all lateral faces are equal.
5. The areas of all side faces are equal.
6. All faces have the same dihedral (flat) angles.
7. A sphere can be described around the pyramid. The center of the circumscribed sphere will be the point of intersection of the perpendiculars that pass through the middle of the edges.
8. A sphere can be inscribed in the pyramid. The center of the inscribed sphere will be the intersection point of the bisectors emanating from the angle between the edge and the base.
9. If the center of the inscribed sphere coincides with the center of the circumscribed sphere, then the sum of the plane angles at the vertex is equal to π or vice versa, one angle is equal to π / n, where n is the number of angles at the base of the pyramid.
The connection of the pyramid with the sphere
A sphere can be described around a pyramid when a polyhedron lies at the base of the pyramid around which a circle can be described (a necessary and sufficient condition). The center of the sphere will be the point of intersection of the planes passing perpendicularly through the midpoints of the side edges of the pyramid.
A sphere can always be described around any triangular or regular pyramid.
A sphere can be inscribed into the pyramid if the bisector planes of the inner dihedral corners of the pyramid intersect at one point (a necessary and sufficient condition). This point will be the center of the sphere.
Connection of a pyramid with a cone
A cone is called inscribed in a pyramid if their tops coincide and the base of the cone is inscribed in the base of the pyramid.
A cone can be inscribed into a pyramid if the apothems of the pyramid are equal to each other.
A cone is called circumscribed around a pyramid if their tops coincide, and the base of the cone is circumscribed around the base of the pyramid.
A cone can be described around the pyramid if all the side edges of the pyramid are equal to each other.
Connection of a pyramid with a cylinder
A pyramid is called inscribed in a cylinder if the top of the pyramid lies on one base of the cylinder, and the base of the pyramid is inscribed in another base of the cylinder.
A cylinder can be described around a pyramid if a circle can be described around the base of the pyramid.
A tetrahedron has four faces and four vertices and six edges, where any two edges do not have common vertices but do not touch.
Each vertex consists of three faces and edges that form triangular corner.
The segment connecting the vertex of the tetrahedron with the center of the opposite face is called median tetrahedron(GM).
Bimedian is the segment connecting the midpoints of opposite edges that are not in contact (KL).
All bimedians and medians of the tetrahedron meet at one point (S). In this case, the bimedians are divided in half, and the medians are in a ratio of 3: 1, starting from the top.
Definition. Acute-angled pyramid- this is a pyramid in which the apothem is more than half the length of the side of the base.
Definition. Obtuse pyramid- this is a pyramid in which the apothem is less than half the length of the side of the base.
Definition. Regular tetrahedron- a tetrahedron in which all four faces are equilateral triangles. It is one of the five regular polygons. In a regular tetrahedron, all dihedral angles (between faces) and trihedral angles (at the vertex) are equal.
Definition. Rectangular tetrahedron is called a tetrahedron with a right angle between three edges at the vertex (the edges are perpendicular). Three faces form rectangular triangular corner and the faces are right-angled triangles, and the base is an arbitrary triangle. The apothem of any facet is equal to half of the side of the base on which the apothem falls.
Definition. Equhedral tetrahedron called a tetrahedron in which the side faces are equal to each other, and the base is a regular triangle. For such a tetrahedron, the faces are isosceles triangles.
Definition. Orthocentric tetrahedron is called a tetrahedron in which all the heights (perpendiculars) that are lowered from the top to the opposite face intersect at one point.
Definition. Star pyramid is called a polyhedron whose base is a star.
Pyramid. Truncated pyramid
Pyramid is called a polyhedron, one of whose faces is a polygon ( base ), and all other faces are triangles with a common vertex ( side faces ) (fig. 15). The pyramid is called correct if its base is a regular polygon and the top of the pyramid is projected to the center of the base (Fig. 16). A triangular pyramid in which all edges are equal is called tetrahedron .
Side rib pyramid is the side of the side face that does not belong to the base Height pyramid is called the distance from its top to the plane of the base. All lateral edges of a regular pyramid are equal to each other, all lateral edges are equal isosceles triangles. The height of the side face of a regular pyramid drawn from the top is called apothem . Diagonal section the section of the pyramid is called a plane passing through two lateral edges that do not belong to one face.
Side surface area pyramid is called the sum of the areas of all side faces. Full surface area called the sum of the areas of all side faces and the base.
Theorems
1. If in a pyramid all side edges are equally inclined to the plane of the base, then the top of the pyramid is projected into the center of the circle circumscribed about the base.
2. If in the pyramid all side edges have equal lengths, then the top of the pyramid is projected into the center of the circle circumscribed about the base.
3. If in the pyramid all the faces are equally inclined to the plane of the base, then the top of the pyramid is projected into the center of the circle inscribed in the base.
To calculate the volume of an arbitrary pyramid, the following formula is correct:
where V- volume;
S main- base area;
H- the height of the pyramid.
For the correct pyramid, the formulas are correct:
where p- base perimeter;
h a- apothem;
H- height;
S full
S side
S main- base area;
V- the volume of the correct pyramid.
Truncated pyramid called the part of the pyramid, enclosed between the base and the secant plane parallel to the base of the pyramid (Fig. 17). Regular truncated pyramid is called the part of a regular pyramid, enclosed between the base and the secant plane parallel to the base of the pyramid.
Foundations truncated pyramids - similar polygons. Side faces - trapezoid. Height a truncated pyramid is the distance between its bases. Diagonal a truncated pyramid is called a segment connecting its vertices that do not lie on the same face. Diagonal section the section of a truncated pyramid is called a plane passing through two lateral edges that do not belong to one face.
For a truncated pyramid, the following formulas are valid:
(4)
where S 1 , S 2 - areas of the upper and lower bases;
S full- total surface area;
S side- lateral surface area;
H- height;
V- the volume of the truncated pyramid.
For a correct truncated pyramid, the formula is correct:
where p 1 , p 2 - perimeters of the bases;
h a- the apothem of the regular truncated pyramid.
Example 1. In a regular triangular pyramid, the dihedral angle at the base is 60º. Find the tangent of the angle of inclination of the side edge to the plane of the base.
Solution. Let's make a drawing (fig. 18).
 |
The pyramid is regular, so at the base there is an equilateral triangle and all side faces are equal isosceles triangles. The dihedral angle at the base is the angle of inclination of the side face of the pyramid to the plane of the base. The linear angle is the angle a between two perpendiculars: and i.e. The top of the pyramid is projected in the center of the triangle (the center of the circumcircle and the inscribed circle in the triangle ABC). The angle of inclination of the lateral rib (for example SB) Is the angle between the edge itself and its projection onto the plane of the base. For rib SB this angle will be the angle SBD... To find the tangent, you need to know the legs SO and OB... Let the length of the segment BD is equal to 3 a... Dot O section BD is divided into parts: and From we find SO: 
From we find: 
Answer:
Example 2. Find the volume of a regular truncated quadrangular pyramid if the diagonals of its bases are cm and cm, and the height is 4 cm.
Solution. To find the volume of the truncated pyramid, we use formula (4). To find the area of the bases, you need to find the sides of the base squares, knowing their diagonals. The sides of the bases are 2 cm and 8 cm, respectively. So the area of the bases and Having substituted all the data in the formula, we calculate the volume of the truncated pyramid:
Answer: 112 cm 3.
Example 3. Find the area of the side face of a regular triangular truncated pyramid, the sides of the bases of which are 10 cm and 4 cm, and the height of the pyramid is 2 cm.
Solution. Let's make a drawing (fig. 19).
The side face of this pyramid is an isosceles trapezoid. To calculate the area of a trapezoid, you need to know the base and height. The bases are given by condition, only the height remains unknown. We will find it from where A 1 E perpendicular from point A 1 on the plane of the lower base, A 1 D- perpendicular from A 1 on AS. A 1 E= 2 cm, since this is the height of the pyramid. To find DE we will make an additional drawing, in which we will depict a top view (fig. 20). Point O- projection of the centers of the upper and lower bases. since (see fig. 20) and On the other hand OK Is the radius of the inscribed circle and 
OM- radius of the inscribed circle:
MK = DE.
By the Pythagorean theorem from
Side face area: 
Answer:
Example 4. At the base of the pyramid lies an isosceles trapezoid, the bases of which a and b (a> b). Each side face forms an angle with the base plane of the pyramid equal to j... Find the total surface area of the pyramid.
Solution. Let's make a drawing (fig. 21). Total surface area of the pyramid SABCD equal to the sum of the areas and the area of the trapezoid ABCD.
Let us use the statement that if all the faces of the pyramid are equally inclined to the plane of the base, then the apex is projected to the center of the circle inscribed in the base. Point O- vertex projection S at the base of the pyramid. Triangle SOD is the orthogonal projection of the triangle CSD on the plane of the base. By the theorem on the area of the orthogonal projection of a plane figure, we get:
Similarly, it means 
Thus, the task was reduced to finding the area of the trapezoid ABCD... Draw a trapezoid ABCD separately (fig. 22). Point O- the center of the circle inscribed in the trapezoid.
Since a circle can be inscribed into a trapezoid, either From, by the Pythagorean theorem, we have
