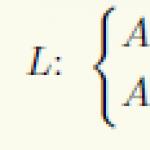Three cases of a straight line and a plane. Mutual arrangement of straight lines and planes

The relative position of a straight line and a plane is determined by the number of common points :

1) if a straight line has two common points with a plane, then it belongs to this plane,

2) if the straight line has one common point with the plane, then the straight line intersects the plane,

3) if the point of intersection of a straight line with a plane is removed to infinity, then the straight line and the plane are parallel.

Problems in which the relative position of various geometric shapes relative to each other is determined are called positional problems.

The straight line belonging to the plane was considered earlier.

Line parallel to plane, if it is parallel to some straight line lying in this plane. To build such a straight line, it is necessary to specify any straight line in the plane and draw the required one parallel to it.

Rice. 1.53 Fig. 1.54 Figure 1.55

Let through the point A(Fig. 1.53) it is necessary to draw a straight line AB parallel to the plane Q given by a triangle CDF. For this, through the frontal projection of the point a / points A let's do a frontal projection a / b / the desired straight line parallel to the frontal projection of any straight line lying in the plane R, eg direct CD (a / b /!!s / d /). Through horizontal projection a points A parallel sd we carry out a horizontal projection aw the required straight line AB (av11 sd). Straight AB parallel to plane R, given a triangle CDF.

Of all the possible positions of a straight line intersecting the plane, we note the case when the straight line is perpendicular to the plane. Consider the properties of the projections of such a straight line.

Rice. 1.56 Fig. 1.57

Straight line perpendicular to plane(a special case of intersection of a straight line with a plane) if it is perpendicular to any straight line in the plane. To construct projections of the perpendicular to a plane in general position, this is not enough without transforming the projections. Therefore, an additional condition is introduced: a straight line is perpendicular to a plane if it is perpendicular to two intersecting main lines(for constructing projections, the condition of projection of a right angle is used). In this case: the horizontal and frontal projections of the perpendicular are perpendicular to the horizontal projection of the horizontal and the frontal projection of the front of the given plane in general position, respectively (Fig. 1.54). When specifying a plane by traces, the projections of the perpendicular are perpendicular, respectively, to the frontal trace, horizontal to the horizontal trace of the plane (Fig. 1.55).

Intersection of a straight line with a projection plane. Consider straight line intersecting plane when the plane is in a private position.

A plane perpendicular to the projection plane (projecting plane) is projected onto it in the form of a straight line. On this straight line (projection of the plane) there must be a corresponding projection of the point at which some straight line intersects this plane (Figure 1.56).

In Figure 1.56, the frontal projection of the point TO intersection of a straight line AB with triangle CDE is defined at the intersection of their frontal projections, since triangle CDE is projected onto the frontal plane in the form of a straight line. Find the horizontal projection of the point of intersection of the straight line with the plane (it lies on the horizontal projection of the straight line). Using the method of competing points, we determine the visibility of the line AB relative to the plane of the triangle CDE on the horizontal projection plane.

Figure 1.59 shows a horizontal projection plane P and the general line AB... Because plane R is perpendicular to the horizontal plane of the projections, then everything that is in it is projected onto the horizontal plane of the projections onto its trace, including the point of its intersection with the straight line AB... Therefore, in the complex drawing we have a horizontal projection of the point of intersection of a straight line with a plane R... By belonging to a point on a straight line, we find the frontal projection of the point of intersection of a straight line AB with plane R... Determine the visibility of the straight line on the frontal plane of the projections.

Rice. 1.58 Fig. 1.59

Figure 1.58 gives a comprehensive drawing for constructing projections of the point of intersection of a straight line AB with a horizontal level G. Frontal plane trace G is its frontal projection. Frontal projection of the point of intersection of the plane G with a straight line AB are defined at the intersection of the frontal projection of the straight line and the frontal trace of the plane. Having a frontal projection of the intersection point, we find the horizontal projection of the intersection point of the straight line AB with plane G.

Figure 1.57 shows a general position plane defined by a triangle CDE and front-projecting straight line AB? intersecting plane at point K. Frontal projection of a point - k / matches dots a / and b/. To construct a horizontal projection of the intersection point, draw through the point K in plane CDE straight line (for example, 1-2 ). Let's build its frontal projection, and then the horizontal one. Point K is the point of intersection of lines AB and 1-2. That is the point K at the same time belongs to the straight line AB and the plane of the triangle and, therefore, is the point of their intersection.

The intersection of two planes. A straight line of intersection of two planes is defined by two points, each of which belongs to both planes, or one point belonging to two planes, and the known direction of the line. In both cases, the task is to find a point common to two planes.

Intersection of projection planes. Two planes can be parallel to each other or intersect. Consider the cases of mutual intersection of planes.

A straight line obtained at the mutual intersection of two planes is completely determined by two points, each of which belongs to both planes, therefore, it is necessary and sufficient to find these two points belonging to the line of intersection of two given planes.

Therefore, in the general case, to construct a line of intersection of two planes, it is necessary to find any two points, each of which belongs to both planes. These points define the line of intersection of the planes. To find each of these two points, you usually have to perform special constructions. But if at least one of the intersecting planes is perpendicular (or parallel) to any projection plane, then the construction of the projection of the line of their intersection is simplified.

Rice. 1.60 Fig. 1.61

If the planes are given by the traces, then it is natural to look for points that define the line of intersection of the planes at the points of intersection of the traces of the same planes in pairs: the line passing through these points is common for both planes, i.e. their line of intersection.

Consider special cases of the location of one (or both) of the intersecting planes.

The complex drawing (Fig. 1.60) shows horizontally projecting planes P and Q. Then the horizontal projection of their intersection line degenerates into a point, and the frontal projection into a straight line perpendicular to the axis ox.

The complex drawing (Fig. 1.61) shows the planes of a particular position: the plane R perpendicular to the horizontal projection plane (horizontal projection plane) and the plane Q- the plane of the horizontal level. In this case, the horizontal projection of their line of intersection will coincide with the horizontal trace of the plane. R, and the frontal - with the frontal trace of the plane Q.

In the case of specifying planes by traces, it is easy to establish that these planes intersect: if at least one pair of traces of the same name intersect, then the planes intersect.

The foregoing refers to the planes defined by intersecting traces. If both planes have traces parallel to each other on the horizontal and frontal planes, then these planes can be parallel or intersect. The relative position of such planes can be judged by constructing a third projection (third trace). If the traces of both planes on the third projection are also parallel, then the planes are parallel to each other. If the traces on the third plane intersect, then the planes specified in space intersect.

The complex drawing (Fig. 1.62) shows the front-projection planes defined by a triangle ABC and DEF... The projection of the intersection line on the frontal projection plane is a point, i.e. since the triangles are perpendicular to the frontal plane of the projections, then their line of intersection is also perpendicular to the frontal plane of the projections. Therefore, the horizontal projection of the line of intersection of triangles ( 12 ) is perpendicular to the axis ox. The visibility of triangle elements on the horizontal projection plane is determined using competing points (3,4).

In the complex drawing (Fig. 1.63) two planes are given: one of which is a triangle ABC general position, the other - a triangle DEF perpendicular to the frontal plane of the projections, i.e. in a private position (front-projection). Frontal projection of the line of intersection of triangles ( 1 / 2 / ) is found on the basis of common points that simultaneously belong to both triangles (everything that is in the front-projecting triangle DEF on the frontal projection will result in a line - its projection onto the frontal plane, including the line of its intersection with the triangle ABC. By belonging of points of intersection to the sides of the triangle ABC, we find the horizontal projection of the line of intersection of the triangles. Using the method of competing points, we determine the visibility of the elements of the triangles on the horizontal projection plane.

Rice. 1.63 Fig. 1.64

Figure 1.64 gives a complex drawing of two planes defined by a triangle in general position. ABC and horizontally projecting plane R given by traces. Since the plane R- horizontally projecting, then everything that is in it, including the line of its intersection with the plane of the triangle ABC, on the horizontal projection will coincide with its

horizontal track. The frontal projection of the line of intersection of these planes is found from the condition that the points of the element (sides) belong to the plane in general position.

In the case of specifying planes in general position not by traces, then to obtain the line of intersection of the planes, the meeting point of the side of one triangle with the plane of the other triangle is sequentially found. If the planes in general position are not specified by triangles, then the intersection line of such planes can be found by introducing alternately two auxiliary secant planes - projecting (for specifying planes with triangles) or level for all other cases.

Intersection of a straight line in general position with a plane in general position. Previously, cases of intersection of planes were considered, when one of them was projecting. Based on this, we can find the point of intersection of a straight line in general position with a plane in general position, by introducing an additional projection plane-mediator.

Before considering the intersection of planes in general position, consider the intersection of a straight line in general position with a plane in general position.

To find the meeting point of a straight line in general position with a plane in general position, it is necessary:

1) enclose a straight line in an auxiliary projection plane,

2) find the line of intersection of the given and auxiliary planes,

define a common point belonging simultaneously to two planes (this is their line of intersection) and a straight line.

Rice. 1.65 Fig. 1.66

Rice. 1.67 Fig. 1.68

The complex drawing (Fig. 1.65) shows a triangle CDE general position and direct AB general position. To find the point of intersection of a straight line with a plane, we conclude a straight line AB Q... Find the intersection line ( 12 ) of the mediator plane Q and a given plane CDE... When constructing a horizontal projection of the intersection line, there is a common point TO, simultaneously belonging to two planes and a given straight line AB... From the belonging of a point to a straight line, we find the frontal projection of the point of intersection of a straight line with a given plane. The visibility of the line elements on the projection planes is determined using competing points.

Figure 1.66 shows an example of finding the meeting point of a straight line AB, which is a horizontal line (a straight line is parallel to the horizontal plane of projections) and a plane R, in general position, given by traces. To find the point of their intersection, the straight line AB lies in the horizontally projecting plane Q. Then proceed as in the above example.

To find the meeting point of a horizontally projecting line AB with a plane in general position (Fig. 1.67), through the meeting point of a straight line with a plane (its horizontal projection coincides with the horizontal projection of the straight line itself) we draw a horizontal line (that is, we tie the point of intersection of a straight line with a plane into a plane R). Having found the frontal projection of the drawn horizontal line in the plane R, mark the frontal projection of the meeting point of the straight line AB with plane R.

To find the line of intersection of planes in general position, defined by traces, it is enough to mark two common points that simultaneously belong to both planes. Such points are the points of intersection of their tracks (Fig. 1.68).

To find the line of intersection of the planes in general position, defined by two triangles (Fig. 1.69), we successively find the point

the side of one triangle meets the plane of another triangle. Taking any two sides from any triangle, enclosing them in the projection planes of the mediators, there are two points that simultaneously belong to both triangles - the line of their intersection.

Figure 1.69 gives a complex drawing of triangles. ABC and DEF general position. To find the line of intersection of these planes:

1. We conclude a side Sun triangle ABC to the front-projection plane S(the choice of planes is completely arbitrary).

2. Find the line of intersection of the plane S and plane DEF – 12 .

3. Mark the horizontal projection of the meeting point (common point of two triangles) TO from intersection 12 and Sun and find its frontal projection on the frontal projection of the straight line Sun.

4. Draw the second auxiliary projection plane Q across the side DF triangle DEF.

5. Find the line of intersection of the plane Q and triangle ABC - 3 4.

6. Mark the horizontal projection of the point L, which is the meeting point of the party DF with the plane of the triangle ABC and find its frontal projection.

7. We connect the projections of the points of the same name TO and L. К L- line of intersection of planes in general position, defined by triangles ABC and DEF.

8. Using the method of competing points, we determine the visibility of the elements of the triangles on the projection planes.

Since the above is valid for the main lines of parallel planes, we can say that planes are parallel if their traces of the same name are parallel(Fig. 1.71).
Figure 1.72 shows the construction of a plane parallel to a given one and passing through a point A. In the first case, through the point A a straight line (frontal) is drawn parallel to a given plane G... Thus, the plane R containing a straight line parallel to a given plane G and parallel to it. In the second case, through the point A a plane is drawn, specified by the main lines from the condition that these lines are parallel to a given plane G.

Mutually perpendicular planes.If one plane contains

at least one straight line perpendicular to another plane, then such

planes are perpendicular. Figure 1.73 shown are mutually perpendicular planes. Figure 1.74 shows the construction of a plane perpendicular to the specified through the point A, using the condition of perpendicularity of a straight line (in this case, the main lines) of the plane.

In the first case, through the point A a frontal is drawn, perpendicular to the plane R, its horizontal trace is built and a horizontal trace of the plane is drawn through it Q, perpendicular to the horizontal plane trace R... Through the resulting vanishing point of the tracks Q X the frontal trace of the plane is drawn Q perpendicular to the frontal plane trace R.

In the second case, a horizontal line is drawn in the plane of the triangle BE and frontal Bf and through a given point A set the plane with intersecting straight lines (main lines), perpendicular to the plane of the triangle. To do this, draw through the point A horizontal and frontal. The horizontal projection of the horizontal line of the desired plane ( N) we draw perpendicular to the horizontal projection of the horizontal of the triangle, the frontal projection of the front of the new plane ( M) - perpendicular to the frontal projection of the frontal triangle.

The relative position of a straight line and a plane in space allows three cases. A straight line and a plane can intersect at one point. They can be parallel. Finally, a straight line can lie in a plane. Clarification of a specific situation for a straight line and a plane depends on the way they are described.

Suppose that the plane π is given by the general equation π: Ax + By + Cz + D = 0, and the line L is given by the canonical equations (x - x 0) / l = (y - y 0) / m = (z - z 0) / n. The equations of the straight line give the coordinates of the point M 0 (x 0; y 0; z 0) on the straight line and the coordinates of the direction vector s = (l; m; n) of this straight line, and the equation of the plane gives the coordinates of its normal vector n = (A; B; C).

If the straight line L and the plane π intersect, then the direction vector s of the straight line is not parallel to the plane π. Hence, the normal vector n of the plane is not orthogonal to the vector s, i.e. their dot product is not zero. Through the coefficients of the equations of the line and the plane, this condition is written in the form of the inequality A1 + Bm + Cn ≠ 0.

If the line and the plane are parallel or the line lies in the plane, then the condition s ⊥ n is satisfied, which in coordinates reduces to the equality Al + Bm + Cn = 0. To separate the cases of "parallel" and "the line belongs to the plane", it is necessary to check whether point of a straight line of a given plane.

Thus, all three cases of relative position of a straight line and a plane are separated by checking the corresponding conditions:

If the line L is given by its general equations:

then the relative position of the straight line and the plane π can be analyzed as follows. From the general equations of the straight line and the general equation of the plane, we compose system of three linear equations with three unknowns

If this system has no solutions, then the line is parallel to the plane. If it has a unique solution, then the line and the plane intersect at a single point. The latter is equivalent to the fact that system identifier (6.6)

nonzero. Finally, if system (6.6) has infinitely many solutions, then the line belongs to the plane.

The angle between a straight line and a plane. The angle φ between the straight line L: (x - x 0) / l = (y - y 0) / m = (z - z 0) / n and the plane π: Ax + By + Cz + D = 0 is in the range from 0 ° (in case of parallelism) to 90 ° (in case of perpendicularity of a straight line and a plane). The sine of this angle is equal to | cosψ |, where ψ is the angle between the direction vector of the straight line s and the normal vector n of the plane (Fig. 6.4). Calculating the cosine of the angle between two vectors in terms of their coordinates (see (2.16)), we obtain

The condition of perpendicularity of the line and the plane is equivalent to the fact that the normal vector of the plane and the direction vector of the line are collinear. Through the coordinates of the vectors, this condition is written in the form of a double equality

Straight can belong to plane, be her parallel or cross plane. A straight line belongs to a plane if two points belonging to a straight line and a plane have the same elevations... Consequence that follows from the above: a point belongs to a plane if it belongs to a straight line lying in this plane.

A straight line is parallel to a plane if it is parallel to a straight line lying in this plane.

Straight line intersecting the plane. To find the point of intersection of a straight line with a plane, it is necessary (Fig. 3.28):

1) draw an auxiliary plane through the given line m T;

2) build a line n intersection of the given plane Σ with the auxiliary plane T;

3) mark the intersection point R, a given straight line m with the line of intersection n.

Consider the problem (Fig. 3.29). The straight line m is given on the plan by the point A 6 and an angle of inclination of 35 °. An auxiliary vertical plane is drawn through this line T, which intersects the plane Σ along the line n (B 2 C 3). Thus, one moves from the relative position of a straight line and a plane to the relative position of two straight lines lying in the same vertical plane. This problem is solved by constructing the profiles of these straight lines. Intersection of straight lines m and n on the profile defines the desired point R... Point elevation R determined by the scale of vertical scales.

A straight line perpendicular to the plane. A straight line is perpendicular to a plane if it is perpendicular to any two intersecting straight lines of this plane. Figure 3.30 shows a straight line m perpendicular to the plane Σ and intersecting it at point A. On the plan, the projection of the straight line m and the horizontals of the plane are mutually perpendicular (a right angle, one side of which is parallel to the plane of the projections, is projected without distortion. Both straight lines lie in the same vertical plane, therefore, the positions of such straight lines are reciprocal in magnitude to each other: l m = l / l u. But l uΣ = lΣ, then l m = l / lΣ, that is, the location of the straight line m is inversely proportional to the location of the plane. Falls near a straight line and a plane are directed in different directions.

3.4. Numerical elevation projections. Surfaces

3.4.1 Polyhedra and curved surfaces. Topographic surface

In nature, many substances have a crystalline structure in the form of polyhedrons. A polyhedron is a collection of flat polygons that do not lie in the same plane, where each side of one of them is simultaneously a side of the other. When depicting a polyhedron, it is enough to indicate the projections of its vertices, connecting them in a certain order with straight lines - the projections of the edges. In this case, visible and invisible edges must be indicated in the drawing. In fig. 3.31 depicts a prism and a pyramid, as well as finding the elevations of points belonging to these surfaces.

A special group of convex polygons is a group of regular polygons in which all faces are equal regular polygons and all polygonal angles are equal. There are five types of regular polygons.

Tetrahedron- a regular quadrangle, bounded by equilateral triangles, has 4 vertices and 6 edges (Fig. 3.32 a).

Hexahedron- regular hexagon (cube) - 8 vertices, 12 edges (Figure 3.32b).

Octahedron- a regular octahedron, bounded by eight equilateral triangles - 6 vertices, 12 edges (Fig. 3.32c).

Dodecahedron- a regular dodecahedron, bounded by twelve regular pentagons, connected by three near each vertex.

It has 20 vertices and 30 edges (Figure 3.32 d).

Icosahedron- a regular twenty-sided triangle, bounded by twenty equilateral triangles, connected by five near each vertex. 12 vertices and 30 edges (Fig. 3.32 e).

When constructing a point lying on a face of a polyhedron, it is necessary to draw a line belonging to this face and mark the projection of the point on its projection.

Conical surfaces are formed by moving a rectilinear generatrix along a curved guide so that in all positions the generatrix passes through a fixed point - the top of the surface. Conical surfaces of a general view on the plan are depicted by a horizontal guide and a vertex. In fig. 3.33 shows the location of the elevation of a point on the surface of a conical surface.

A straight circular cone is depicted by a series of concentric circles drawn at regular intervals (Figure 3.34a). An elliptical cone with a circular base - a series of eccentric circles (Figure 3.34 b)

Spherical surfaces. A spherical surface is referred to as surfaces of revolution. It is formed by rotating a circle around its diameter. On the plan, the spherical surface is defined by the center TO and the projection of one of its contours (the equator of the sphere) (Fig. 3.35).

Topographic surface. The topographic surface is referred to as geometrically irregular surfaces, since it does not have a geometric law of formation. To characterize the surface, the position of its characteristic points relative to the projection plane is determined. In fig. 3.3 b and an example of a section of a topographic surface is given, on which the projections of its individual points are shown. Such a plan, although it makes it possible to get an idea of ​​the shape of the depicted surface, is, however, not very clear. To give the drawing greater clarity and thereby facilitate its reading, the projections of points with the same elevations are connected by smooth curved lines, which are called contours (isolines) (Fig. 3.36 b).

The horizontals of a topographic surface are sometimes also defined as the lines of intersection of this surface with horizontal planes spaced from each other at the same distance (Figure 3.37). The difference in elevation between two adjacent contours is called the section height.

The more accurate the image of the topographic surface is, the smaller the difference in elevation between two adjacent contours. On plans, contours are closed within the drawing or outside it. On steeper slopes of the surface, the projections of the contour lines converge, on gentle ones, their projections diverge.

The shortest distance between the projections of two adjacent contours on the plan is called the inception. In fig. 3.38 through point A several straight line segments are drawn on the topographic surface AND YOU and AD... They all have different angles of incidence. The largest angle of incidence has a segment AS, the laying of which has a minimum value. Therefore, it will be the projection of the line of incidence of the surface in this place.

In fig. 3.39 is an example of constructing a projection of a line of incidence through a given point A... From point A 100, as from the center, draw an arc of a circle tangent to the nearest horizontal line at the point T 90... Point At 90, horizontal h 90, will belong to the fall line. From point T 90 draw an arc touching the next horizontal at the point C 80, etc. The drawing shows that the line of incidence of the topographic surface is a broken line, each link of which is perpendicular to the horizontal, passing through the lower end of the link, which has a lower mark.

3.4.2 Intersection of a conical surface by a plane

If the cutting plane passes through the vertex of the conical surface, then it intersects it along the straight lines that form the surface. In all other cases, the section line will be a flat curve: a circle, an ellipse, etc. Consider the case of intersection of a conical surface by a plane.

Example 1. Construct a projection of the line of intersection of a circular cone Φ ( h about , S 5) with the plane Ω parallel to the generatrix of the conical surface.

A conical surface for a given location of the plane intersects in a parabola. Interpolating the generatrix t we build horizontals of a circular cone - concentric circles with a center S 5 . Then we define the points of intersection of the contour lines of the same name of the plane and the cone (Fig. 3.40).

3.4.3. Intersection of a topographic surface with a plane and a straight line

The case of intersection of a topographic surface with a plane is most often encountered in solving geological problems. In fig. 3.41 an example of constructing the intersection of a topographic surface with the plane Σ is given. Looking for a curve m are determined by the intersection points of the contours of the same name of the plane and the topographic surface.

In fig. 3.42 an example of constructing a true view of a topographic surface with a vertical plane Σ is given. The sought line m is determined by the points A, B, C… The intersection of the contour lines of the topographic surface with the cutting plane Σ. On the plan, the projection of the curve degenerates into a straight line that coincides with the projection of the plane: m≡ Σ. The profile of the curve m is built taking into account the location of the projections of its points on the plan, as well as their elevations.

3.4.4. Equal slope surface

A surface of equal slope is a ruled surface, all rectilinear generators of which make a constant angle with the horizontal plane. Such a surface can be obtained by moving a straight circular cone with an axis perpendicular to the plane of the plan, so that its vertex would slide along a certain guide, and the axis would remain vertical in any position.

In fig. 3.43 shows a surface of equal slope (i = 1/2), which is guided by a spatial curve A, B, C, D.

Graduation plane. As examples, consider the plane of the slopes of the roadway.

Example 1. The longitudinal slope of the roadway i = 0, the slope of the embankment slope i n = 1: 1.5, (Fig. 3.44a). It is required to draw horizontals through 1m. The solution boils down to the following. We draw the scale of the slope of the plane perpendicular to the edge of the roadway, mark the points at a distance equal to an interval of 1.5 m, taken from a linear scale, and determine the marks 49, 48 and 47. Through the obtained points we draw the contours of the slope parallel to the edge of the road.

Example 2. The longitudinal slope of the road i ≠ 0, the slope of the embankment slope i n = 1: 1.5, (Figure 3.44b). The plane of the road surface is graduated. The slope of the roadbed is graded as follows. At a point with a top 50.00 (or another point), place the apex of the cone, describe a circle with a radius equal to the interval of the embankment slope (in our example l= 1.5m). The elevation of this contour of the cone will be one less than the elevation of the vertex, i.e. 49m. We draw a number of circles, we get the marks of the contour lines 48, 47, in relation to which from the points of the edge with marks 49, 48, 47 we draw the horizontal lines of the embankment slope.

Graduation of surfaces.

Example 3. If the longitudinal slope of the road i = 0 and the slope of the embankment slope i n = 1: 1.5, then the horizontal slopes are drawn through the points of the slope scale, the interval of which is equal to the interval of the embankment slopes (Figure 3.45a). The distance between two projections of adjacent contour lines in the direction of the common norm (slope scale) is the same everywhere.

Example 4. If the longitudinal slope of the road is i ≠ 0, and the slope of the embankment slope is i n = 1: 1.5, (Figure 3.45b), then the horizontal lines are constructed in the same way, except that the horizontal slopes are drawn not in straight lines, but in curves.

3.4.5. Determination of the earthwork limit line

Since most soils are unable to maintain vertical walls, slopes (artificial structures) have to be built. The slope imparted by the slope depends on the soil.

In order to give a plot of the earth's surface the appearance of a plane with a certain slope, you need to know the line of limits for earthwork and zero works. This line that delimits the planned area is represented by the intersection of embankment slopes and cut slopes with the specified topographic surface.

Since each surface (including a flat one) is depicted using contour lines, the intersection line of surfaces is constructed as a set of intersection points of contour lines with the same elevations. Let's look at some examples.

Example 1. In fig. 3.46 is given an earthen structure in the form of a truncated quadrangular pyramid, standing on a plane N... Upper base ABCD the pyramid has a mark 4m and the sizes of the sides 2 × 2.5 m... The side faces (embankment slopes) have a slope of 2: 1 and 1: 1, the direction of which is shown by arrows.

It is necessary to build a line of intersection of the slopes of the structure with the plane N and between themselves, as well as build a longitudinal profile along the axis of symmetry.

First, a diagram of slopes, intervals and scales of laying, given slopes, is built. Perpendicular to each side of the site, the scales of the slopes of the slopes are drawn at specified intervals, after which the projections of the contour lines with the same elevations of the adjacent faces are the intersection lines of the slopes, which are the projections of the side edges of this pyramid.

The lower base of the pyramid coincides with the zero contours of the slopes. If this earthen structure is crossed by a vertical plane Q, in the section you get a broken line - the longitudinal profile of the structure.

Example 2... Construct a line of intersection of the pit slopes with a flat slope and with each other. Bottom ( ABCD) of the pit is a rectangular area with an elevation of 10 m and dimensions of 3 × 4 m. The axis of the site makes an angle of 5 ° with the south-north line. The slopes of the excavations have the same slopes of 2: 1 (Figure 3.47).

The zero works line is established according to the terrain plan. It is built according to the intersection points of the same projections of the contours of the surfaces under consideration. At the points of intersection of the contour lines of the slopes and the topographic surface with the same elevations, the line of intersection of the slopes is found, which are the projections of the side edges of this pit.

In this case, the side slopes of the excavations are adjacent to the bottom of the excavation. Line abcd- the sought line of intersection. Aa, Bb, Сс, Dd- the edges of the pit, the line of intersection of the slopes with each other.

4. Questions for self-control and tasks for independent work on the topic "Rectangular projections"

Point

4.1.1. The essence of the projection method.

4.1.2. What is Point Projection?

4.1.3. How are the projection planes called and designated?

4.1.4. What are the lines of the projection connection in the drawing and how are they located in the drawing in relation to the projection axes?

4.1.5. How to create a third (profile) projection of a point?

4.1.6. Construct three projections of points A, B, C on a three-picture drawing, write down their coordinates and fill in the table.

4.1.7. Construct the missing projection axes, x A = 25, y A = 20. Construct a profile projection of point A.

4.1.8. Construct three projections of points along their coordinates: A (25,20,15), B (20,25,0) and C (35,0,10). Specify the position of points in relation to planes and projection axes. Which of the points is closer to the plane P 3?

4.1.9. Material points A and B begin to fall at the same time. Where will point B be when point A touches the ground? Determine the visibility of the points. Construct points at a new position.

4.1.10. Construct three projections of point A, if the point lies in the plane P 3, and the distance from it to the plane P 1 is 20 mm, to the plane P 2 - 30 mm. Write down the coordinates of the point.

Straight

4.2.1. How can a straight line be specified in a drawing?

4.2.2. What line is called a straight line in general position?

4.2.3. What position can a straight line occupy with respect to the projection planes?

4.2.4. When does the projection of a straight line turn into a point?

4.2.5. What is characteristic of a complex drawing of a straight level?

4.2.6. Determine the relative position of these straight lines.

a… b a… b a… b

4.2.7. Construct a projection of a straight line segment AB 20 mm long, parallel to the planes: a) P 2; b) P 1; c) the Ox axis. Designate the angles of inclination of the segment to the projection planes.

4.2.8. Construct a projection of the segment AB according to the coordinates of its ends: A (30,10,10), B (10,15,30). Construct projections of point C dividing the segment in relation to AC: CB = 1: 2.

4.2.9. Determine and record the number of edges of a given polyhedron and their position relative to the projection planes.

4.2.10. Draw a horizontal line and a frontal line through point A, intersecting line m.

4.2.11. Determine the distance between line b and point A

4.2.12. Construct a projection of a segment AB 20 mm long passing through point A and perpendicular to the plane a) P 2; b) P 1; c) P 3.

Stereometry

Mutual arrangement of straight lines and planes

In space

Parallelism of lines and planes

Two lines in space are called parallel if they lie in the same plane and do not intersect.

The line and the plane are called parallel if they do not overlap.

The two planes are called parallel if they do not overlap.

Lines that do not intersect and do not lie in the same plane are called interbreeding .

Parallelism of a straight line and a plane... If a straight line that does not belong to a plane is parallel to some straight line in this plane, then it is parallel to the plane itself.

Parallelism of planes... If two intersecting straight lines of one plane are respectively parallel to two straight lines of another plane, then these planes are parallel.

Crossing straight lines... If one of the two lines lies in a plane, and the other intersects this plane at a point that does not belong to the first line, then these lines are crossed.

Theorem on parallel straight lines and parallel planes.

1. Two lines parallel to the third line are parallel.

2. If one of two parallel lines intersects a plane, then the other line also intersects this plane.

3. Through a point outside the given straight line, you can draw a straight line parallel to the given one, and only one.

4. If a line is parallel to each of two intersecting planes, then it is parallel to their line of intersection.

5. If two parallel planes intersect with a third plane, then the intersection lines are parallel.

6. Through a point that does not lie in the given plane, you can draw a plane parallel to the given one, and only one.

7. Two planes parallel to the third are parallel to each other.

8. Sections of parallel straight lines, enclosed between parallel planes, are equal.

Angles between lines and planes

The angle between a straight line and a plane called the angle between a straight line and its projection onto a plane (angle in Fig. 1).

The angle between crossing lines is called the angle between intersecting straight lines parallel to the given intersecting straight lines.

Dihedral angle is called a figure formed by two half-planes with a common straight line. The half-planes are called facets , straight line - edge dihedral angle.

Linear angle dihedral angle is called the angle between the half-lines belonging to the faces of the dihedral angle, originating from one point on the edge and perpendicular to the edge (angle in Fig. 2).

The degree (radian) measure of the dihedral angle is equal to the degree (radian) measure of its linear angle.

Perpendicularity of lines and planes

Two lines are called perpendicular if they intersect at right angles.

A straight line intersecting a plane is called perpendicular this plane, if it is perpendicular to any straight line in the plane passing through the point of intersection of this straight line and the plane.

The two planes are called perpendicular if intersecting, they form right dihedral angles.

The sign of perpendicularity of a line and a plane... If a straight line intersecting a plane is perpendicular to two intersecting straight lines in this plane, then it is perpendicular to the plane.

The sign of perpendicularity of two planes... If a plane passes through a straight line perpendicular to another plane, then these planes are perpendicular.

Theorems on perpendicular lines and planes.

1. If the plane is perpendicular to one of two parallel straight lines, then it is perpendicular to the other.

2. If two straight lines are perpendicular to the same plane, then they are parallel.

3. If a straight line is perpendicular to one of two parallel planes, then it is perpendicular to the other.

4. If two planes are perpendicular to the same straight line, then they are parallel.

Perpendicular and oblique

Theorem... If a perpendicular and oblique lines are drawn from one point outside the plane, then:

1) inclined, having equal projections, are equal;

2) of the two inclined ones, the one with the larger projection is larger;

3) equal oblique have equal projections;

4) of the two projections, the larger is the one that corresponds to the larger oblique.

Three perpendicular theorem... In order for a straight line lying in a plane to be perpendicular to an inclined one, it is necessary and sufficient that this straight line be perpendicular to the inclined projection (Fig. 3).

The theorem on the area of ​​the orthogonal projection of a polygon onto a plane. The area of ​​the orthogonal projection of the polygon onto the plane is equal to the product of the area of ​​the polygon by the cosine of the angle between the plane of the polygon and the plane of the projection.

Construction.

1. On a plane a we draw a straight line a.

3. In the plane b through the point A let's draw a straight line b parallel to the straight line a.

4. Constructed a straight line b parallel to plane a.

Proof. On the basis of parallelism of a straight line and a plane, a straight line b parallel to plane a since it is parallel to the straight line a belonging to the plane a.

Study. The problem has an infinite number of solutions, since the straight line a in plane a is selected arbitrarily.

Example 2. Determine how far from the plane the point is A if straight AB crosses the plane at an angle of 45º, the distance from the point A to the point V belonging to the plane is equal to cm?

Solution. Let's make a picture (fig. 5):

AS- perpendicular to the plane a, AB- inclined, angle ABC- the angle between the straight line AB and plane a... Triangle ABC- rectangular since AS- perpendicular. Desired distance from point A to the plane - this is the leg AS right triangle. Knowing the angle and the hypotenuse cm, we will find the leg AS:

Answer: 3 cm.

Example 3. Determine at what distance from the plane of an isosceles triangle is a point 13 cm distant from each of the vertices of the triangle, if the base and height of the triangle are 8 cm each?

Solution. Let's make a drawing (fig. 6). Point S removed from points A, V and WITH the same distance. Means oblique SA, SB and SC equal, SO- the common perpendicular of these oblique. By the oblique and projection theorem AO = BO = CO.

Point O- the center of a circle circumscribed about a triangle ABC... Let's find its radius:

where Sun- base;

AD Is the height of this isosceles triangle.

Finding the sides of a triangle ABC from a right triangle ABD by the Pythagorean theorem:

Now we find OV:

Consider a triangle SOB: SB= 13 cm, OV= = 5 cm. Find the length of the perpendicular SO by the Pythagorean theorem:

Answer: 12 cm.

Example 4. Parallel planes are given a and b... Through point M that does not belong to any of them, direct a and b that cross a in points A 1 and V 1, and the plane b- in points A 2 and V 2. Find A 1 V 1 if it is known that MA 1 = 8 cm, A 1 A 2 = 12 cm, A 2 V 2 = 25 cm.

Solution. Since the condition does not say how the point is located relative to both planes M, then two options are possible: (Fig. 7, a) and (Fig. 7, b). Let's consider each of them. Two intersecting lines a and b set the plane. This plane intersects two parallel planes a and b on parallel lines A 1 V 1 and A 2 V 2 according to Theorem 5 on parallel straight lines and parallel planes.

Triangles MA 1 V 1 and MA 2 V 2 are similar (angles A 2 MV 2 and A 1 MV 1 - vertical, corners MA 1 V 1 and MA 2 V 2 - internal criss-crossing at parallel lines A 1 V 1 and A 2 V 2 and secant A 1 A 2). The proportionality of the sides follows from the similarity of triangles:

Option a):

Option b):

Answer: 10 cm and 50 cm.

Example 5. Through point A plane g a direct AB forming an angle with the plane a... Through a straight line AB drawn plane r forming with the plane g injection b... Find the angle between the projection of a straight line AB on the plane g and plane r.

Solution. Let's make a drawing (fig. 8). From point V drop the perpendicular to the plane g... Linear angle of dihedral angle between planes g and r Is the angle Straight AD DBC, on the basis of the perpendicularity of the straight line and the plane, since and On the basis of the perpendicularity of the planes, the plane r perpendicular to the plane of the triangle DBC since it goes through a straight line AD... We construct the desired angle by dropping the perpendicular from the point WITH on the plane r, denote it Find the sine of this corner of a right triangle MYSELF... Introduce an auxiliary segment a = BC... Out of the triangle ABC: Out of a triangle Navy find

Then the required angle

Answer:

Self-help assignments

Level I

1.1. Draw a straight line through a point perpendicular to two given intersecting straight lines.

1.2. Determine how many different planes you can draw:

1) through three different points;

2) through four different points, none of which lie on the same plane?

1.3. Through the vertices of the triangle ABC lying in one of two parallel planes, parallel straight lines are drawn that intersect the second plane at points A 1 , V 1 , WITH 1 . Prove the equality of triangles ABC and A 1 V 1 WITH 1 .

1.4. From the top A rectangle ABCD restored perpendicular AM to its plane.

1) prove that the triangles MBC and MDC- rectangular;

2) indicate among the segments MB, MC, MD and MA the segment of the largest and smallest length.

1.5. The faces of one dihedral angle are respectively parallel to the faces of the other. Determine what is the relationship between the values ​​of these dihedral angles.

1.6. Find the value of the dihedral angle if the distance from the point taken on one face to the edge is 2 times the distance from the point to the plane of the second face.

1.7. From a point at a distance from the plane, two equal inclined ones are drawn, forming an angle of 60º. Oblique projections are mutually perpendicular. Find the lengths of the slopes.

1.8. From the top V square ABCD restored perpendicular BE to the plane of the square. The angle of inclination of the plane of the triangle ACE to the plane of the square is j, the side of the square is a ACE.

II level

2.1. Through a point that does not belong to any of the two intersecting lines, draw a line intersecting both given lines.

2.2. Parallel lines a, b and with do not lie in the same plane. Through point A on a straight line a drawn perpendiculars to straight lines b and with intersecting them, respectively, at points V and WITH... Prove that the straight line Sun perpendicular to straight lines b and with.

2.3. Across the top A right triangle ABC drawn plane parallel Sun... Triangle legs AS= 20 cm, Sun= 15 cm. The projection of one of the legs onto the plane is 12 cm. Find the projection of the hypotenuse.

2.4. In one of the faces of the dihedral angle equal to 30º, there is a point M... The distance from it to the edge of the corner is 18 cm. Find the distance from the projection of the point M on the second face to the first face.

2.5. Segment ends AB belong to the faces of a dihedral angle equal to 90º. Distance from points A and V to the edge are equal respectively AA 1 = 3 cm, BB 1 = 6 cm, the distance between points on the edge Find the length of the line AB.

2.6. From a point at a distance from the plane a, two oblique ones are drawn, forming angles of 45º and 30º with the plane, and the angle between them is 90º. Find the distance between the sloped bases.

2.7. The sides of the triangle are 15 cm, 21 cm and 24 cm. Point M removed from the plane of the triangle by 73 cm and is at the same distance from its vertices. Find this distance.

2.8. From the center O a circle inscribed in a triangle ABC, the perpendicular is restored to the plane of the triangle OM... Find the distance from the point M to the sides of the triangle if AB = BC = 10 cm, AS= 12 cm, OM= 4 cm.

2.9. Distances from point M to the sides and tops of the right angle are respectively 4 cm, 7 cm and 8 cm.Find the distance from the point M to the plane of the right angle.

2.10. Through the base AB isosceles triangle ABC the plane is drawn at an angle b to the plane of the triangle. Vertex WITH removed from the plane at a distance a... Find the area of ​​a triangle ABC if the base AB an isosceles triangle is equal to its height.

III level

3.1. Rectangle layout ABCD with the parties a and b bent diagonally BD so that the planes of the triangles BAD and BCD become mutually perpendicular. Find the length of the segment AS.

3.2. Two rectangular trapezoids with angles of 60º lie in perpendicular planes and have a greater common base. The large sides are 4 cm and 8 cm. Find the distance between the vertices of the straight lines and the vertices of the obtuse corners of the trapezoids if the vertices of their acute corners coincide.

3.3. A given cube ABCDA 1 B 1 C 1 D 1 . Find the angle between the straight line CD 1 and plane BDC 1 .

3.4. On the edge AB Cuba ABCDA 1 B 1 C 1 D 1 point taken R Is the middle of this rib. Construct a section of a cube with a plane passing through the points C 1 PD and find the area of ​​this section if the edge of the cube is a.

3.5. Across the side AD rectangle ABCD drawn plane a so that the diagonal BD makes an angle of 30º with this plane. Find the angle between the plane of the rectangle and the plane a, if AB = a, AD = b... Determine at what ratio a and b the problem has a solution.

3.6. Find the locus of points equidistant from the straight lines defined by the sides of the triangle.

Prism. Parallelepiped

Prism is called a polyhedron whose two faces are equal n-gons (grounds) lying in parallel planes, and the remaining n faces are parallelograms (side faces) . Side rib a prism is the side of the side face that does not belong to the base.

A prism whose side edges are perpendicular to the planes of the bases is called straight prism (Fig. 1). If the side edges are not perpendicular to the planes of the bases, then the prism is called oblique . Correct A prism is a straight prism, the bases of which are regular polygons.

Height prism is called the distance between the planes of the bases. Diagonal prism is called a segment that connects two vertices that do not belong to the same face. Diagonal section the section of a prism is called a plane passing through two lateral edges that do not belong to one face. Perpendicular section the section of a prism is called a plane perpendicular to the lateral edge of the prism.

Lateral surface area prism is called the sum of the areas of all side faces. Full surface area called the sum of the areas of all faces of the prism (i.e. the sum of the areas of the side faces and the areas of the bases).

For an arbitrary prism, the following formulas are valid:

where l- the length of the side rib;

H- height;

P

Q

S side

S full

S main- the area of ​​the bases;

V Is the volume of the prism.

For a straight prism, the following formulas are correct:

where p- base perimeter;

l- the length of the side rib;

H- height.

Parallelepiped called a prism, the base of which is a parallelogram. A parallelepiped with side edges perpendicular to the bases is called direct (fig. 2). If the side edges are not perpendicular to the bases, then the parallelepiped is called oblique ... A straight parallelepiped, the base of which is a rectangle, is called rectangular. A rectangular parallelepiped with all edges equal is called cube.

The faces of a parallelepiped that do not have common vertices are called opposing ... The lengths of the edges outgoing from one vertex are called measurements parallelepiped. Since a parallelepiped is a prism, its main elements are defined in the same way as they are defined for prisms.

Theorems.

1. The diagonals of the parallelepiped intersect at one point and are halved by it.

2. In a rectangular parallelepiped, the square of the diagonal length is equal to the sum of the squares of its three dimensions:

3. All four diagonals of a rectangular parallelepiped are equal to each other.

For an arbitrary parallelepiped, the following formulas are true:

where l- the length of the side rib;

H- height;

P- the perimeter of the perpendicular section;

Q- The area of ​​the perpendicular section;

S side- lateral surface area;

S full- total surface area;

S main- the area of ​​the bases;

V Is the volume of the prism.

For a straight parallelepiped, the following formulas are true:

where p- base perimeter;

l- the length of the side rib;

H- the height of the straight parallelepiped.

For a rectangular parallelepiped, the following formulas are true:

where p- base perimeter;

H- height;

d- diagonal;

a, b, c- measurements of the parallelepiped.

For a cube, the following formulas are correct:

where a- rib length;

d Is the diagonal of the cube.

Example 1. The diagonal of a rectangular parallelepiped is 33 dm, and its dimensions are related as 2: 6: 9. Find the dimensions of the parallelepiped.

Solution. To find the dimensions of the parallelepiped, we use formula (3), i.e. by the fact that the square of the hypotenuse of a rectangular parallelepiped is equal to the sum of the squares of its measurements. Let us denote by k proportionality coefficient. Then the dimensions of the parallelepiped will be 2 k, 6k and 9 k... Let's write the formula (3) for the problem data:

Solving this equation for k, we get:

This means that the dimensions of the parallelepiped are 6 dm, 18 dm and 27 dm.

Answer: 6 dm, 18 dm, 27 dm.

Example 2. Find the volume of an inclined triangular prism, the base of which is an equilateral triangle with a side of 8 cm, if the lateral edge is equal to the side of the base and is inclined at an angle of 60º to the base.

Solution . Let's make a drawing (fig. 3).

In order to find the volume of an inclined prism, it is necessary to know its base area and height. The area of ​​the base of this prism is the area of ​​an equilateral triangle with a side of 8 cm. Let's calculate it:

The height of a prism is the distance between its bases. From the top A 1 of the upper base, we lower the perpendicular to the plane of the lower base A 1 D... Its length will be the height of the prism. Consider D A 1 AD: since this is the angle of inclination of the side rib A 1 A to the plane of the base, A 1 A= 8 cm.From this triangle we find A 1 D:

Now we calculate the volume by the formula (1):

Answer: 192 cm 3.

Example 3. The lateral edge of a regular hexagonal prism is 14 cm. The area of ​​the largest diagonal section is 168 cm 2. Find the total surface area of ​​the prism.

Solution. Let's make a drawing (fig. 4)

Largest Diagonal Section - Rectangle AA 1 DD 1, since the diagonal AD regular hexagon ABCDEF is the greatest. In order to calculate the area of ​​the lateral surface of the prism, it is necessary to know the side of the base and the length of the lateral rib.

Knowing the area of ​​the diagonal section (rectangle), we find the diagonal of the base.

Since, then

Since then AB= 6 cm.

Then the perimeter of the base is:

Let us find the area of ​​the lateral surface of the prism:

The area of ​​a regular hexagon with a side of 6 cm is:

Find the total surface area of ​​the prism:

Answer:

Example 4. The base of the rectangular parallelepiped is a rhombus. The areas of the diagonal sections are 300 cm 2 and 875 cm 2. Find the area of ​​the side surface of a parallelepiped.

Solution. Let's make a drawing (fig. 5).

Let us denote the side of the rhombus through a, the diagonals of the rhombus d 1 and d 2, the height of the parallelepiped h... To find the area of ​​the lateral surface of a straight parallelepiped, multiply the perimeter of the base by the height: (formula (2)). Base perimeter p = AB + BC + CD + DA = 4AB = 4a, because ABCD- rhombus. H = AA 1 = h... That. Need to find a and h.

Consider diagonal sections. AA 1 SS 1 - rectangle, one side of which is the diagonal of the rhombus AS = d 1, the second is a lateral rib AA 1 = h, then

Similarly for the section BB 1 DD 1 we get:

Using the property of a parallelogram such that the sum of the squares of the diagonals is equal to the sum of the squares of all its sides, we obtain the equality We obtain the following:

Let us express and substitute in the third from the first two equalities. We get: then

1.3. In an inclined triangular prism, a cross-section is drawn perpendicular to the side edge equal to 12 cm. In the resulting triangle, two sides with lengths of cm and 8 cm form an angle of 45 °. Find the area of ​​the lateral surface of the prism.

1.4. The base of a straight parallelepiped is a rhombus with a side of 4 cm and an acute angle of 60 °. Find the diagonals of the parallelepiped if the side edge is 10 cm long.

1.5. The base of a straight parallelepiped is a square with a diagonal equal to cm. The side edge of the parallelepiped is 5 cm. Find the total surface area of ​​the parallelepiped.

1.6. The base of the inclined parallelepiped is a rectangle with sides of 3 cm and 4 cm. The side edge equal to cm is inclined to the base plane at an angle of 60 °. Find the volume of the parallelepiped.

1.7. Calculate the surface area of ​​a rectangular parallelepiped if two edges and a diagonal emanating from one vertex are 11 cm, 13 cm and 13 cm, respectively.

1.8. Determine the weight of a stone column in the shape of a rectangular parallelepiped with dimensions of 0.3 m, 0.3 m and 2.5 m, if the specific gravity of the material is 2.2 g / cm 3.

1.9. Find the area of ​​the diagonal section of a cube if the diagonal of its face is dm.

1.10. Find the volume of a cube if the distance between its two vertices that do not lie on the same face is cm.

II level

2.1. The base of the inclined prism is an equilateral triangle with a side of cm. The lateral rib is inclined to the base plane at an angle of 30 °. Find the cross-sectional area of ​​the prism passing through the side edge and the height of the prism if it is known that one of the vertices of the upper base is projected to the middle of the side of the lower base.

2.2. The base of the inclined prism is an equilateral triangle ABC with a side equal to 3 cm. The vertex A 1 is projected into the center of triangle ABC. Rib AA 1 makes an angle of 45 ° with the base plane. Find the area of ​​the lateral surface of the prism.

2.3. Calculate the volume of an oblique triangular prism if the sides of the base are 7 cm, 5 cm and 8 cm, and the height of the prism is equal to the lower height of the triangle base.

2.4. The diagonal of a regular quadrangular prism is inclined to the side face at an angle of 30 °. Find the angle of inclination to the plane of the base.

2.5. The base of the straight prism is an isosceles trapezoid, the bases of which are 4 cm and 14 cm, and the diagonal is 15 cm. The two side faces of the prism are squares. Find the total surface area of ​​the prism.

2.6. The diagonals of a regular hexagonal prism are 19 cm and 21 cm. Find its volume.

2.7. Find the dimensions of a rectangular parallelepiped with a diagonal of 8 inches and forming angles of 30 ° and 40 ° with the side faces.

2.8. The diagonals of the base of the rectangular parallelepiped are 34 cm and 38 cm, and the areas of the side faces are 800 cm 2 and 1200 cm 2. Find the volume of the parallelepiped.

2.9. Determine the volume of a rectangular parallelepiped in which the diagonals of the side faces extending from one vertex are 4 cm and 5 cm and form an angle of 60 °.

2.10. Find the volume of a cube if the distance from its diagonal to the edge that does not intersect with it is mm.

III level

3.1. In a regular triangular prism, a section is drawn through the side of the base and the middle of the opposite side edge. The area of ​​the base is 18 cm 2, and the diagonal of the side face is inclined to the base at an angle of 60 °. Find the cross-sectional area.

3.2. At the base of the prism lies the square ABCD, all vertices of which are equidistant from the top A 1 of the upper base. The angle between the lateral rib and the plane of the base is 60 °. The side of the base is 12 cm. Construct a section of the prism by a plane, passing through the vertex C, perpendicular to the edge AA 1 and find its area.

3.3. The base of the straight prism is an isosceles trapezoid. The area of ​​the diagonal section and the areas of the parallel side faces are respectively 320 cm 2, 176 cm 2 and 336 cm 2. Find the area of ​​the lateral surface of the prism.

3.4. The area of ​​the base of a straight triangular prism is 9 cm 2, the area of ​​the side faces is 18 cm 2, 20 cm 2 and 34 cm 2. Find the volume of the prism.

3.5. Find the diagonals of a rectangular parallelepiped, knowing that the diagonals of its edges are 11 cm, 19 cm and 20 cm.

3.6. The angles formed by the diagonal of the base of the rectangular parallelepiped with the side of the base and the diagonal of the parallelepiped are equal to a and b, respectively. Find the area of ​​the side surface of a parallelepiped if its diagonal is d.

3.7. The area of ​​that section of the cube, which is a regular hexagon, is equal to cm 2. Find the surface area of ​​a cube.

Remote element.

a remote element.

• a) have no common points;

Theorem.

Section designation

GOST 2.305-2008 provides for the following requirements for the designation of the section:

1. The position of the cutting plane is indicated in the drawing by a section line.

2. An open line must be used for the section line (thickness from S to 1.5S, line length 8-20 mm).

3. In the case of a complex section, the strokes are also drawn at the intersection of the secant planes with each other.

4. Arrows should be placed on the initial and final strokes, indicating the direction of view, arrows should be drawn at a distance of 2-3 mm from the outer end of the stroke.

5. The dimensions of the arrows should correspond to those shown in Figure 14.

6. The starting and ending strokes must not intersect the outline of the corresponding image.

7. At the beginning and end of the section line, and, if necessary, at the intersection of the secant planes, put the same capital letter of the Russian alphabet. The letters are applied near the arrows indicating the direction of sight and at the intersections from the side of the outer corner (Figure 24).

Figure 24 - Examples of section designation

8. The incision should be marked with an inscription of the "А-А" type (always with two letters separated by a dash).

9. When the secant plane coincides with the plane of symmetry of the object as a whole, and the corresponding images are located on the same sheet in direct projection connection and are not separated by any other images, the position of the secant plane is not marked for horizontal, frontal and profile cuts, and the incision is not accompanied by an inscription.

10. Frontal and profile cuts, as a rule, are given the position corresponding to the one adopted for the given object in the main image of the drawing.

11. Horizontal, frontal and profile cuts can be located in place of the corresponding main views.

12. It is allowed to place a section at any place in the drawing field, as well as with a rotation with the addition of a conventional graphic designation - the Rotated icon (Figure 25).

Figure 25 - Conventional graphic designation - "Rotated" icon

Cross-section designation is similar to the designation of the sections and consists of traces of the cutting plane and an arrow indicating the direction of view, as well as a letter affixed to the outside of the arrow (Figure 1c, Figure 3). The extended section is not labeled and the section plane is not shown if the section line coincides with the section symmetry axis, and the section itself is located on the continuation of the section plane trace or in the gap between the parts of the view. For a symmetrical superimposed section, the cut plane is also not shown. If the section is asymmetric and is located in a gap or is superimposed (Figure 2 b), the section line is drawn with arrows, but they are not indicated by letters.

The section is allowed to be positioned with a turn, supplying the inscription above the section with the word "turned". For several identical sections related to one object, the section lines are designated by the same letter and one section is drawn. In cases where the section is obtained consisting of separate parts, cuts should be used.

General line

A straight line in general position (Figure 2.2) is called a straight line that is not parallel to any of the given projection planes. Any segment of such a straight line is distortedly projected in the given system of projection planes. The angles of inclination of this straight line to the projection planes are also distorted.

Rice. 2.2.

Direct private clauses
The straight lines of a particular position include straight lines parallel to one or two projection planes.
Any line (straight or curve) parallel to the projection plane is called a level line. In engineering graphics, there are three main level lines: horizontal, frontal and profile lines.

Rice. 2.3-a

A horizontal line is any line parallel to the horizontal plane of the projections (Fig. 2, 3-a). The front projection of the horizontal is always perpendicular to the communication lines. Any horizontal segment on the horizontal projection plane is projected in true value. The true value is projected onto this plane and the angle of inclination of the horizontal (straight line) to the frontal plane of the projections. As an example, Fig. 2, 3-a shows a visual image and a complex drawing of the horizontal h inclined to the plane NS 2 at an angle b .
Rice. 2.3-b

Frontal is called a line parallel to the frontal plane of the projections (Figure 2.3-b). The horizontal projection of the front is always perpendicular to the communication lines. Any segment of the frontal line on the frontal plane of projections is projected into the true value. In true magnitude, it is projected onto this plane and the angle of inclination of the front (straight line) to the horizontal plane of projections (angle a).
Rice. 2.3-in

The profile line is a line parallel to the profile plane of the projections (Fig. 2, 3-c). The horizontal and frontal projections of the profile line are parallel to the communication lines of these projections. Any segment of the profile line (straight line) is projected onto the profile plane in true size. On the same plane, the angles of inclination of the profile line to the projection planes are projected in the true value NS 1 and NS 2. When defining a profile line in a complex drawing, it is necessary to indicate two points of this line.

Level lines parallel to two projection planes will be perpendicular to the third projection plane. Such straight lines are called projecting. There are three main projecting lines: horizontally, frontally and profile projecting lines.
Rice. 2.3-g Rice. 2.3-d Rice. 2.3th

A horizontally projecting straight line (Fig. 2, 3-d) is called a straight line perpendicular to the plane NS 1 . Any segment of this straight line is projected onto the plane NS NS 1 - to the point.

A frontally projecting straight line (Fig. 2 Z-e) is called a straight line perpendicular to the plane NS 2. Any segment of this straight line is projected onto the plane NS 1 without distortion, but on a plane NS 2 - to the point.

A profile projecting straight line (Fig. 2, 3-e) is called a straight line perpendicular to the plane NS 3, i.e. straight line parallel to the projection planes NS 1 and NS 2. Any segment of this straight line is projected on the plane NS 1 and NS 2 without distortion, but on a plane NS 3 - to the point.

Principal lines in a plane

Among the straight lines belonging to the plane, a special place is occupied by straight lines that occupy a particular position in space:

1. Horizontals h - straight lines lying in a given plane and parallel to the horizontal projection plane (h // P1) (Fig.6.4).

Figure 6.4 Horizontal

2. Frontals f - straight lines located in the plane and parallel to the frontal plane of the projections (f // P2) (Figure 6.5).

Figure 6.5 Front

3. Profile straight lines p - straight lines that are in this plane and are parallel to the profile plane of the projections (p // P3) (Figure 6.6). It should be noted that the traces of the plane can also be attributed to the main lines. The horizontal trace is the horizontal of the plane, the frontal is the frontal and the profile is the profile line of the plane.

Figure 6.6 Profile line

4. The line of the greatest slope and its horizontal projection form a linear angle j, which measures the dihedral angle made up by this plane and the horizontal projection plane (Figure 6.7). Obviously, if a straight line does not have two points in common with a plane, then it is either parallel to the plane or intersects it.

Figure 6.7 Line of greatest slope

Kinematic way of forming surfaces. Sets the surface in the drawing.

In engineering graphics, a surface is considered as a set of successive positions of a line moving in space according to a certain law. In the process of surface formation, line 1 can remain unchanged or change its shape.
For clarity of the surface image in a complex drawing, it is advisable to set the law of displacement graphically in the form of a family of lines (a, b, c). The law of displacement of line 1 can be specified by two (a and b) or one (a) lines and additional conditions that clarify the law of displacement 1.
Moving line 1 is called generatrix, fixed lines a, b, c - guides.
Let us consider the process of surface formation using the example shown in Figure 3.1.
Here, straight line 1 is taken as the generator. The law of displacement of the generator is given by the direction a and the straight line b. In this case, it is meant that the generator 1 slides along the guide a, all the time remaining parallel to the straight line b.
This method of surface formation is called kinematic. With its help, you can form and define various surfaces in the drawing. In particular, Figure 3.1 shows the most general case of a cylindrical surface.

Rice. 3.1.

Another way to form a surface and display it in a drawing is to define the surface by a set of points or lines belonging to it. In this case, the points and lines are chosen so that they make it possible to determine the shape of the surface with a sufficient degree of accuracy and solve various problems on it.
The set of points or lines that define a surface are called wireframes.
Depending on how the surface frame is defined, points or lines, wireframes are divided into point and linear.
Figure 3.2 shows a surface frame consisting of two orthogonally located families of lines a1, a2, a3, ..., an and b1, b2, b3, ..., bn.

Rice. 3.2.

Conical sections.

TAPERED SECTIONS, plane curves, which are obtained by the intersection of a straight circular cone with a plane that does not pass through its vertex (Fig. 1). From the point of view of analytical geometry, a conical section is a locus of points that satisfy a second-order equation. Except for the degenerate cases discussed in the last section, conic sections are ellipses, hyperbolas, or parabolas.

Conical sections are often found in nature and technology. For example, the orbits of planets orbiting the Sun are elliptical. A circle is a special case of an ellipse in which the major axis is equal to the minor axis. A parabolic mirror has the property that all incident rays parallel to its axis converge at one point (focus). This is used in most reflector telescopes using parabolic mirrors, as well as in radar antennas and special microphones with parabolic reflectors. A beam of parallel rays emanates from a light source placed at the focus of a parabolic reflector. Therefore, parabolic mirrors are used in high-power floodlights and car headlights. Hyperbola is a graph of many important physical relationships, for example, Boyle's law (linking the pressure and volume of an ideal gas) and Ohm's law, which specifies electric current as a function of resistance at constant voltage.

EARLY HISTORY

The discoverer of conical sections is supposedly Menechm (4th century BC), a student of Plato and teacher of Alexander the Great. Menechm used a parabola and an isosceles hyperbola to solve the problem of doubling a cube.

Treatises on conical sections written by Aristeas and Euclid at the end of the 4th century. BC, were lost, but materials from them entered the famous Conical sections of Apollonius of Perga (c. 260–170 BC), which have survived to our time. Apollonius abandoned the requirement for the perpendicularity of the secant plane of the generatrix of the cone and, by varying the angle of its inclination, obtained all conical sections from one circular cone, straight or inclined. We also owe Apollonius the modern names of curves - ellipse, parabola and hyperbola.

In his constructions, Apollonius used a two-cavity circular cone (as in Fig. 1), so for the first time it became clear that a hyperbola is a curve with two branches. Since the time of Apollonius, conic sections have been divided into three types, depending on the inclination of the secant plane to the generatrix of the cone. An ellipse (Fig. 1, a) is formed when the cutting plane intersects all generatrices of the cone at the points of one of its cavities; parabola (Fig. 1, b) - when the cutting plane is parallel to one of the tangent planes of the cone; hyperbola (Fig. 1, c) - when the cutting plane intersects both cavities of the cone.

CONSTRUCTION OF TAPERED SECTIONS

Studying conic sections as intersections of planes and cones, ancient Greek mathematicians considered them as trajectories of points on a plane. It was found that an ellipse can be defined as a locus of points, the sum of the distances from which to two given points is constant; parabola - as a locus of points equidistant from a given point and a given straight line; hyperbola - as a locus of points, the difference in distances from which to two given points is constant.

These definitions of conic sections as plane curves suggest a way to construct them using a stretched thread.

Ellipse.

If the ends of a thread of a given length are fixed at points F1 and F2 (Fig. 2), then the curve described by the tip of a pencil sliding along the tightly stretched thread has the shape of an ellipse. Points F1 and F2 are called the focal points of the ellipse, and the segments V1V2 and v1v2 between the points of intersection of the ellipse with the coordinate axes - the major and minor axes. If points F1 and F2 coincide, then the ellipse turns into a circle.

rice. 2 Ellipsis

Hyperbola.

When constructing a hyperbola, point P, the tip of the pencil, is fixed on a thread that freely slides along the pins set at points F1 and F2, as shown in Fig. 3, a. The distances are chosen so that the PF2 segment is longer than the PF1 segment by a fixed amount less than the F1F2 distance. In this case, one end of the thread passes under the peg F1 and both ends of the thread pass over the peg F2. (The tip of the pencil should not slide along the thread, so it must be secured by making a small loop on the thread and threading the point into it.) We draw one branch of the hyperbola (PV1Q), making sure that the thread remains taut all the time, and pulling both ends down beyond the point F2, and when point P is below the segment F1F2, hold the thread at both ends and carefully etch (i.e. release) it. We draw the second branch of the hyperbola (PўV2Qў), having previously changed the roles of the pins F1 and F2.

rice. 3 hyperbole

The branches of the hyperbola approach two straight lines that intersect between the branches. These straight lines, called the asymptotes of the hyperbola, are constructed as shown in Fig. 3, b. The slopes of these lines are equal to ± (v1v2) / (V1V2), where v1v2 is the segment of the bisector of the angle between the asymptotes, perpendicular to the segment F1F2; the segment v1v2 is called the conjugate axis of the hyperbola, and the segment V1V2 is called its transverse axis. Thus, the asymptotes are the diagonals of a rectangle with sides passing through the four points v1, v2, V1, V2 parallel to the axes. To draw this rectangle, you need to specify the location of points v1 and v2. They are at the same distance equal to

from the point of intersection of the axes O. This formula assumes the construction of a right-angled triangle with legs Ov1 and V2O and hypotenuse F2O.

If the asymptotes of the hyperbola are mutually perpendicular, then the hyperbola is called isosceles. Two hyperbolas that have common asymptotes, but with rearranged transverse and conjugate axes, are called mutually conjugate.

Parabola.

Focuses of the ellipse and hyperbola were already known to Apollonius, but the focus of a parabola was apparently first established by Papp (2nd half of the 3rd century), who defined this curve as the locus of points equidistant from a given point (focus) and a given straight line, which is called the headmistress. The construction of a parabola using a stretched thread, based on Papp's definition, was proposed by Isidor Miletsky (6th century). Place the ruler so that its edge coincides with the directrix LLў (Fig. 4), and attach to this edge leg AC of the drawing triangle ABC. Fix one end of the thread of length AB at the vertex B of the triangle, and the other at the focus of the parabola F. Pulling the thread with the tip of the pencil, press the tip at the variable point P to the free leg AB of the drawing triangle. As the triangle moves along the ruler, point P will describe an arc of a parabola with focus F and directrix LLў, since the total length of the thread is AB, the thread segment is adjacent to the free leg of the triangle, and therefore the remaining segment of the thread PF should be equal to the remaining parts of leg AB, i.e. PA. The point of intersection of the V parabola with the axis is called the apex of the parabola, the line passing through F and V is the axis of the parabola. If you draw a straight line perpendicular to the axis through the focus, then the segment of this straight line cut off by the parabola is called the focal parameter. For an ellipse and a hyperbola, the focal parameter is determined in the same way.

ANSWERS TO TICKETS: № 1 (not completely), 2 (not completely), 3 (not completely), 4, 5, 6, 7, 12, 13, 14 (not completely), 16, 17, 18, 20, 21 , 22, 23, 26,

Remote element.

When making drawings, in some cases, it becomes necessary to construct an additional separate image of any part of an object that requires explanations in terms of shape, size or other data. This image is called a remote element. It is usually performed enlarged. The detail can be laid out as a view or as a cut.

When building a detail, the corresponding place of the main image is marked with a closed solid thin line, usually an oval or circle, and denoted with a capital letter of the Russian alphabet on the leader line shelf. For the extension element, a record is made as type A (5: 1). In fig. 191 shows an example of the execution of a remote element. It is placed as close as possible to the corresponding place on the image of the object.

1. Method of rectangular (orthogonal) projection. Basic invariant properties of rectangular projection. Epure Monge.

Orthogonal (rectangular) projection is a special case of parallel projection, when all projection rays are perpendicular to the projection plane. Orthogonal projections have all the properties of parallel projections, but with rectangular projection, the projection of a segment, if it is not parallel to the plane of projections, is always less than the segment itself (Fig. 58). This is due to the fact that the segment itself in space is the hypotenuse of a right-angled triangle, and its projection is a leg: A "B" = ABcos a.

In rectangular projection, a right angle is projected in full size when both sides of it are parallel to the projection plane, and when only one of its sides is parallel to the projection plane, and the other side is not perpendicular to this projection plane.

Mutual arrangement of a straight line and a plane.

A straight line and a plane in space can:

• a) have no common points;
• b) have exactly one common point;
• c) have at least two common points.

In fig. 30 shows all of these possibilities.

In case a) straight line b is parallel to the plane: b || ...

In case b) the straight line l intersects the plane at one point O; l = O.

In case c) the straight line a belongs to the plane: a or a.

Theorem. If the line b is parallel to at least one line a belonging to the plane, then the line is parallel to the plane.

Suppose that line m intersects the plane at point Q. If m is perpendicular to every straight line in the plane passing through point Q, then line m is called perpendicular to the plane.

Tram rails illustrate the belonging of straight lines to the plane of the earth. Power lines are parallel to the plane of the earth, and tree trunks are examples of straight lines crossing the surface of the earth, some perpendicular to the plane of the earth, others not perpendicular (oblique).