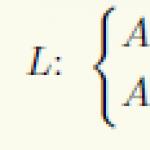A method for solving linear inhomogeneous differential equations of higher orders with constant coefficients by the method of variation of the Lagrange constants is considered. The Lagrange method is also applicable to solving any linear inhomogeneous equations if the fundamental system of solutions of the homogeneous equation is known.
ContentSee also:
Lagrange method (variation of constants)
Consider a linear inhomogeneous differential equation with constant coefficients of an arbitrary n-th order:
(1)
.
The method of variation of the constant, which we considered for a first-order equation, is also applicable to equations of higher orders.
The solution is carried out in two stages. In the first step, we discard the right-hand side and solve the homogeneous equation. As a result, we get a solution containing n arbitrary constants. At the second stage, we vary the constants. That is, we consider that these constants are functions of the independent variable x and find the form of these functions.
Although we consider equations with constant coefficients here, but Lagrange's method is also applicable to solving any linear inhomogeneous equations... For this, however, the fundamental system of solutions of the homogeneous equation must be known.
Step 1. Solving the homogeneous equation
As in the case of first-order equations, we first look for a general solution to the homogeneous equation, equating the inhomogeneous right-hand side to zero:
(2)
.
The general solution to such an equation has the form:
(3)
.
Here are arbitrary constants; - n linearly independent solutions to homogeneous equation (2), which form a fundamental system of solutions to this equation.
Step 2. Variation of constants - replacement of constants with functions
In the second step, we will tackle the variation of constants. In other words, we will replace constants with functions of the independent variable x:
.
That is, we are looking for a solution to the original equation (1) in the following form:
(4)
.
If we substitute (4) into (1), then we get one differential equation for n functions. Moreover, we can relate these functions by additional equations. Then you get n equations, from which you can determine n functions. Additional equations can be constructed in various ways. But we will do it so that the solution has the most simple form. For this, during differentiation, it is necessary to equate to zero the terms containing derivatives of functions. Let's demonstrate this.
To substitute the proposed solution (4) into the original equation (1), we need to find the derivatives of the first n orders of the function written in the form (4). We differentiate (4), applying the rules for differentiating the sum and the product:
.
Let's group the members. First, we write out terms with derivatives from, and then - terms with derivatives from:
.
Let us impose the first condition on the functions:
(5.1)
.
Then the expression for the first derivative with respect to will have a simpler form:
(6.1)
.
We find the second derivative in the same way:
.
Let us impose the second condition on the functions:
(5.2)
.
Then
(6.2)
.
Etc. In additional conditions, we set the terms containing the derivatives of the functions to zero.
Thus, if you choose the following additional equations for the functions:
(5.k) ,
then the first derivatives with respect to will have the simplest form:
(6.k) .
Here .
Find the n -th derivative:
(6.n)
.
Substitute into the original equation (1):
(1)
;
.
Let us take into account that all functions satisfy equation (2):
.
Then the sum of the terms containing give zero. As a result, we get:
(7)
.
As a result, we got a system of linear equations for the derivatives:
(5.1)
;
(5.2)
;
(5.3)
;
. . . . . . .
(5.n-1) ;
(7 ′) .
Solving this system, we find expressions for the derivatives as a function of x. Integrating, we get:
.
Here are constants that are no longer dependent on x. Substituting into (4), we obtain the general solution of the original equation.
Note that we have nowhere used the fact that the coefficients a i are constant to determine the values of the derivatives. That's why Lagrange's method is applicable to solving any linear inhomogeneous equations if the fundamental system of solutions of the homogeneous equation (2) is known.
Examples of
Solve the equations by the method of variation of constants (Lagrange).
Solution examples>>>
Solving higher-order equations by the Bernoulli method
Solution of higher order linear inhomogeneous differential equations with constant coefficients by linear substitution
Lecture 44. Linear inhomogeneous equations of the second order. Method of variation of arbitrary constants. Linear inhomogeneous equations of the second order with constant coefficients. (special right side).
Social transformations. State and Church.
The social policy of the Bolsheviks was largely dictated by their class approach. By a decree of November 10, 1917, the estate system was destroyed, pre-revolutionary ranks, titles and awards were abolished. The electivity of judges has been established; secularization of civil states was carried out. Free education and medical care were established (decree of October 31, 1918). Women were given equal rights with men (decrees of December 16 and 18, 1917). The marriage decree introduced the institution of civil marriage.
By a decree of the Council of People's Commissars of January 20, 1918, the church was separated from the state and from the education system. Most of the church property has been confiscated. Patriarch Tikhon of Moscow and All Russia (elected on November 5, 1917) on January 19, 1918 anathematized Soviet power and called for a fight against the Bolsheviks.
Consider the second-order linear inhomogeneous equation
The structure of the general solution to such an equation is determined by the following theorem:
Theorem 1. The general solution of the inhomogeneous equation (1) is represented as the sum of some particular solution of this equation and the general solution of the corresponding homogeneous equation
Proof... It is necessary to prove that the sum
is the general solution of equation (1). Let us first prove that function (3) is a solution to equation (1).
Substituting the sum into equation (1) instead of at, will have
Since there is a solution to equation (2), the expression in the first brackets is identically equal to zero. Since there is a solution to equation (1), the expression in the second brackets is equal to f (x)... Therefore, equality (4) is an identity. Thus, the first part of the theorem is proved.
Let us prove the second statement: expression (3) is general solution of equation (1). We must prove that the arbitrary constants included in this expression can be chosen so that the initial conditions are satisfied:
whatever the numbers x 0, y 0 and (if only x 0 was taken from the area where functions a 1, a 2 and f (x) continuous).
Noticing what can be represented in the form. Then, based on conditions (5), we will have
Let's solve this system and define C 1 and C 2... Let's rewrite the system as:
Note that the determinant of this system is the Wronski determinant for the functions at 1 and at 2 at the point x = x 0... Since these functions are linearly independent by hypothesis, the Vronsky determinant is not equal to zero; therefore, system (6) has a definite solution C 1 and C 2, i.e. there are such values C 1 and C 2, for which formula (3) defines a solution to equation (1) that satisfies the given initial conditions. Q.E.D.
Let us turn to the general method for finding particular solutions of an inhomogeneous equation.
Let us write the general solution of the homogeneous equation (2)
We will seek a particular solution to the inhomogeneous equation (1) in the form (7), considering C 1 and C 2 as some as yet unknown functions from NS.
Let us differentiate equality (7):
Let us choose the required functions C 1 and C 2 so that the equality
If this additional condition is taken into account, then the first derivative takes the form
Differentiating this expression now, we find:
Substituting into equation (1), we obtain
The expressions in the first two parentheses vanish because y 1 and y 2- solutions to a homogeneous equation. Consequently, the last equality takes the form
Thus, function (7) will be a solution to the inhomogeneous equation (1) if the functions C 1 and C 2 satisfy equations (8) and (9). Let us compose a system of equations from equations (8) and (9).
Since the determinant of this system is the Wronski determinant for linearly independent solutions y 1 and y 2 equation (2), then it is not equal to zero. Therefore, solving the system, we find as definite functions of NS:
Solving this system, we find where, as a result of integration, we obtain. Next, we substitute the found functions into the formula, we obtain the general solution of the inhomogeneous equation, where are arbitrary constants.
The method of variation of arbitrary constants is used to solve inhomogeneous differential equations. This lesson is intended for those students who are already more or less well versed in the topic. If you are just starting to get acquainted with DU, i.e. If you are a teapot, I recommend starting with the first lesson: Differential equations of the first order. Examples of solutions... And if you are already finishing, please discard the possible preconceived notion that the method is difficult. Because it's simple.
In what cases is the method of variation of arbitrary constants applied?
1) The method of variation of an arbitrary constant can be used to solve linear non-uniform DE of the 1st order... Since the equation is of the first order, then the constant (constant) is also one.
2) The method of variation of arbitrary constants is used to solve some linear inhomogeneous equations of the second order... Two constants vary here.
It is logical to assume that the lesson will consist of two paragraphs…. I wrote this proposal, and for 10 minutes I was painfully thinking what other smart crap I could add for a smooth transition to practical examples. But for some reason, there are no thoughts after the holidays, although he did not seem to abuse anything. Therefore, let's go straight to the first paragraph.
Variation method of an arbitrary constant
for a linear inhomogeneous first-order equation
Before considering the method of variation of an arbitrary constant, it is advisable to be familiar with the article Linear differential equations of the first order... In that lesson, we practiced first solution non-uniform DE of the 1st order. Let me remind you that this first solution is called replacement method or Bernoulli method(not to be confused with Bernoulli equation!!!)
We will now consider second solution- method of variation of an arbitrary constant. I will give just three examples, and I will take them from the above lesson. Why so little? Because in fact the solution in the second way will be very similar to the solution in the first way. In addition, according to my observations, the method of variation of arbitrary constants is used less often than the method of replacement.
Example 1
![]()
(Diffur from Example # 2 of the lesson Linear inhomogeneous DE of the 1st order)
Solution: This equation is linear inhomogeneous and has a familiar form: ![]()
The first step is to solve a simpler equation: ![]()
That is, we stupidly zero out the right side - instead of writing zero.
The equation ![]() I'll call auxiliary equation.
I'll call auxiliary equation.
In this example, you need to solve the following auxiliary equation:
Before us separable equation, the solution of which (hopefully) is no longer difficult for you: 
Thus: ![]() - general solution of the auxiliary equation.
- general solution of the auxiliary equation.
In the second step replace constant of some yet unknown function that depends on "x":
Hence the name of the method - we vary the constant. Alternatively, the constant may be some function that we have to find now.
V original inhomogeneous equation ![]() we will replace:
we will replace:
Substitute and ![]() into the equation
into the equation ![]() :
:
Control moment - the two terms on the left cancel out... If this does not happen, you should look for the error above.
As a result of the replacement, an equation with separable variables is obtained. Separate variables and integrate.
What a blessing, exhibitors are also declining:
Add the "normal" constant to the found function:
At the final stage, we recall our replacement:
Function just found!
So the general solution is: 
Answer: common decision: ![]()
If you print out two solutions, you will easily notice that in both cases we found the same integrals. The only difference is in the solution algorithm.
Now for something more complicated, I'll comment on the second example:
Example 2
Find the general solution to the differential equation ![]()
(Diffur from Example # 8 of the lesson Linear inhomogeneous DE of the 1st order)
Solution: Let us bring the equation to the form ![]() :
:
Let us zero the right-hand side and solve the auxiliary equation:
General solution of the auxiliary equation:
In the inhomogeneous equation, we make the replacement:
According to the rule of product differentiation: ![]()
Substitute and ![]() into the original inhomogeneous equation:
into the original inhomogeneous equation:
The two terms on the left side are canceling out, which means we are on the right track: 
We integrate by parts. A tasty letter from the formula for integration by parts has already been used in the solution, so we use, for example, the letters "a" and "be":
![]()
Now we recall the replacement carried out:
Answer: common decision:
And one example for a do-it-yourself solution:
Example 3
Find a particular solution to the differential equation corresponding to a given initial condition.
,
(Diffur from Example # 4 of the lesson Linear inhomogeneous DE of the 1st order)
Solution:
This DE is linear inhomogeneous. We use the method of variation of arbitrary constants. Let's solve the auxiliary equation:
Separate variables and integrate: 
Common decision: ![]()
In the inhomogeneous equation, we will replace: ![]()
Let's perform the substitution: 
So the general solution is: ![]()
Let us find a particular solution corresponding to the given initial condition: ![]()
Answer: private solution:
The solution at the end of the lesson can serve as a rough example for finishing the assignment.
Variation method of arbitrary constants
for a linear inhomogeneous second-order equation
with constant coefficients
We often heard the opinion that the method of variation of arbitrary constants for a second-order equation is not an easy thing. But my guess is the following: most likely, the method seems difficult to many, since it is not so common. But in reality there are no special difficulties - the course of the decision is clear, transparent, understandable. And beautiful.
To master the method, it is desirable to be able to solve inhomogeneous second-order equations by selecting a particular solution in the form of the right-hand side. This method is discussed in detail in the article. Inhomogeneous DE of the 2nd order... Recall that a second-order linear inhomogeneous equation with constant coefficients has the form:
The selection method, which was considered in the above lesson, works only in a limited number of cases when polynomials, exponents, sines, cosines are on the right side. But what to do when on the right, for example, fraction, logarithm, tangent? In such a situation, the method of variation of constants comes to the rescue.
Example 4
Find the general solution of the second order differential equation ![]()
Solution: There is a fraction on the right side of this equation, so we can immediately say that the method of selecting a particular solution does not work. We use the method of variation of arbitrary constants.
Nothing foreshadows a thunderstorm, the beginning of the solution is completely ordinary:
Find common decision corresponding homogeneous equations: ![]()
Let's compose and solve the characteristic equation: ![]()
![]() - the conjugate complex roots are obtained, so the general solution is:
- the conjugate complex roots are obtained, so the general solution is:
Pay attention to the record of the general solution - if there are brackets, then we expand them.
Now we do practically the same trick as for the first-order equation: we vary the constants, replacing them with unknown functions. That is, general solution to heterogeneous we will seek equations in the form:
Where - yet unknown functions.

It looks like a landfill for household waste, but now we will sort everything.
Derivatives of functions act as unknowns. Our goal is to find derivatives, and the found derivatives must satisfy both the first and second equations of the system.
Where do the "games" come from? The stork brings them. We look at the general solution obtained earlier and write down:
Let's find the derivatives:
With the left parts sorted out. What's on the right?
Is the right side of the original equation, in this case:
The coefficient is the coefficient at the second derivative:
In practice, almost always, and our example is no exception.
Everything has cleared up, now you can create a system: 
The system is usually decided by Cramer's formulas using a standard algorithm. The only difference is that instead of numbers, we have functions.
Let us find the main determinant of the system: 
If you have forgotten how the determinant "two by two" is revealed, refer to the lesson How to calculate the determinant? The link leads to the board of shame =)
So: it means that the system has a unique solution.
Find the derivative: 
But that's not all, so far we have found only the derivative.
The function itself is restored by integration:
Let's deal with the second function: 
![]()
![]()
Here we add a "normal" constant
At the final stage of the solution, we recall in what form we were looking for the general solution of the inhomogeneous equation? In such:
The functions you are looking for have just been found! ![]()
It remains to perform the substitution and write down the answer:
Answer: common decision:
In principle, the brackets could be expanded in the answer.
Full verification of the answer is performed according to the standard scheme, which was discussed in the lesson Inhomogeneous DE of the 2nd order... But the verification will not be easy, since it is necessary to find rather heavy derivatives and carry out a cumbersome substitution. This is an unpleasant feature when you are dealing with diffusion like this.
Example 5
Solve a differential equation by varying arbitrary constants
![]()
This is an example for a do-it-yourself solution. In fact, the right side is also a fraction. We recall the trigonometric formula, by the way, it will need to be applied in the course of the solution.
The method of variation of arbitrary constants is the most versatile method. They can solve any equation that is solved by the method of selecting a particular solution by the view of the right side... The question arises, why not use the method of variation of arbitrary constants there too? The answer is obvious: the selection of a private solution, which was considered in the lesson Inhomogeneous second order equations, significantly speeds up the solution and shortens the writing - no fucking with determinants and integrals.
Consider two examples with the Cauchy problem.
Example 6
Find a particular solution of the differential equation corresponding to the given initial conditions
![]() ,
, ![]()
Solution: Again fraction and exponent in an interesting place.
We use the method of variation of arbitrary constants.
Find common decision corresponding homogeneous equations: ![]()
![]() - different real roots are obtained, so the general solution is:
- different real roots are obtained, so the general solution is:
General solution to heterogeneous we seek equations in the form:, where - yet unknown functions.
Let's compose the system: 
In this case:
,
Find derivatives: ![]() ,
, ![]()
![]()
Thus: 
We solve the system using Cramer's formulas:
, which means that the system has a unique solution.


We restore the function by integrating:
Used here method of bringing a function under the differential sign.


We restore the second function by integrating: ![]()
Such an integral is solved variable replacement method:
From the replacement itself, we express:
Thus: ![]()
![]()
This integral can be found by the method of selection of a full square, but in the examples with differs, I prefer to expand the fraction method of undefined coefficients:
Both functions are found:
As a result, the general solution to the inhomogeneous equation is:
Let us find a particular solution satisfying the initial conditions ![]() .
.
Technically, the search for a solution is carried out in the standard way, which was discussed in the article Inhomogeneous differential equations of the second order.
Hold on, now we will find the derivative of the found common solution:
Here is such a disgrace. It is not necessary to simplify it; it is easier to immediately compose a system of equations. According to the initial conditions ![]() :
:

Substitute the found values of the constants ![]() into a general solution:
into a general solution:
In the response, the logarithms can be packed a little.
Answer: private solution: ![]()
As you can see, difficulties can arise in integrals and derivatives, but not in the algorithm of the method of variation of arbitrary constants itself. It was not I who intimidated you, this is all Kuznetsov's collection!
For relaxation, a final, simpler example for a do-it-yourself solution:
Example 7
Solve the Cauchy problem
![]() ,
, ![]()
An example is simple, but creative, when you make a system, take a close look at it before deciding ;-),
![]()


![]()
As a result, the general solution is:
Let us find a particular solution corresponding to the initial conditions ![]() .
.
![]()

Let's substitute the found values of the constants into the general solution:
Answer: private solution:
Consider now the linear inhomogeneous equation
. (2)
Let y 1, y 2, .., y n be the fundamental system of solutions, and be the general solution of the corresponding homogeneous equation L (y) = 0. Similarly to the case of first-order equations, we will seek a solution to Eq. (2) in the form
. (3)
Let us make sure that a solution in this form exists. To do this, we substitute the function into the equation. To substitute this function into the equation, we find its derivatives. The first derivative is  . (4)
. (4)
When calculating the second derivative, four terms will appear on the right-hand side of (4), when calculating the third derivative, eight terms will appear, and so on. Therefore, for the convenience of further calculations, the first term in (4) is assumed to be zero. With this in mind, the second derivative is  . (5)
. (5)
For the same reasons as before, in (5) we also set the first term equal to zero. Finally, the nth derivative is  . (6)
. (6)
Substituting the obtained values of the derivatives into the original equation, we have  . (7)
. (7)
The second term in (7) is equal to zero, since the functions y j, j = 1,2, .., n, are solutions of the corresponding homogeneous equation L (y) = 0. Combining with the previous one, we obtain a system of algebraic equations for finding the functions C "j (x)  (8)
(8)
The determinant of this system is the Wronski determinant of the fundamental system of solutions y 1, y 2, .., y n of the corresponding homogeneous equation L (y) = 0 and therefore is not equal to zero. Therefore, there is a unique solution to system (8). Having found it, we obtain the functions C "j (x), j = 1,2, ..., n, and, consequently, C j (x), j = 1,2, ..., n Substituting these values in (3), we obtain a solution to a linear inhomogeneous equation.
The described method is called the method of variation of an arbitrary constant or the Lagrange method.
Example # 1. Find the general solution of the equation y "" + 4y "+ 3y = 9e -3 x. Consider the corresponding homogeneous equation y" "+ 4y" + 3y = 0. The roots of its characteristic equation r 2 + 4r + 3 = 0 are equal to -1 and - 3. Therefore, the fundamental system of solutions to the homogeneous equation consists of the functions y 1 = e - x and y 2 = e -3 x. We seek the solution of the inhomogeneous equation in the form y = C 1 (x) e - x + C 2 (x) e -3 x. To find the derivatives C "1, C" 2, we compose the system of equations (8)
C ′ 1 e -x + C ′ 2 e -3x = 0
-C ′ 1 e -x -3C ′ 2 e -3x = 9e -3x
solving which, we find, Integrating the obtained functions, we have ![]()
We finally get
Example No. 2. Solve linear differential equations of the second order with constant coefficients by the method of variation of arbitrary constants: ![]()
y (0) = 1 + 3ln3
y ’(0) = 10ln3
Solution:
This differential equation refers to linear differential equations with constant coefficients.
We will seek a solution to the equation in the form y = e rx. To do this, we compose the characteristic equation of a linear homogeneous differential equation with constant coefficients:
r 2 -6 r + 8 = 0
D = (-6) 2 - 4 1 8 = 4
Roots of the characteristic equation: r 1 = 4, r 2 = 2
Consequently, the fundamental system of solutions is made up of the functions: y 1 = e 4x, y 2 = e 2x
The general solution to the homogeneous equation is: y = C 1 e 4x + C 2 e 2x
Search for a particular solution by the method of variation of an arbitrary constant.
To find the derivatives C "i, we compose a system of equations:
C ′ 1 e 4x + C ′ 2 e 2x = 0
C ′ 1 (4e 4x) + C ′ 2 (2e 2x) = 4 / (2 + e -2x)
Let us express C "1 from the first equation:
C "1 = -c 2 e -2x
and substitute in the second. As a result, we get:
C "1 = 2 / (e 2x + 2e 4x)
C "2 = -2e 2x / (e 2x + 2e 4x)
We integrate the obtained functions C "i:
C 1 = 2ln (e -2x +2) - e -2x + C * 1
C 2 = ln (2e 2x +1) - 2x + C * 2
Since y = C 1 e 4x + C 2 e 2x, then we write the obtained expressions in the form:
C 1 = (2ln (e -2x +2) - e -2x + C * 1) e 4x = 2 e 4x ln (e -2x +2) - e 2x + C * 1 e 4x
C 2 = (ln (2e 2x +1) - 2x + C * 2) e 2x = e 2x ln (2e 2x +1) - 2x e 2x + C * 2 e 2x
Thus, the general solution of the differential equation has the form:
y = 2 e 4x ln (e -2x +2) - e 2x + C * 1 e 4x + e 2x ln (2e 2x +1) - 2x e 2x + C * 2 e 2x
or
y = 2 e 4x ln (e -2x +2) - e 2x + e 2x ln (2e 2x +1) - 2x e 2x + C * 1 e 4x + C * 2 e 2x
Let's find a particular solution provided:
y (0) = 1 + 3ln3
y ’(0) = 10ln3
Substituting x = 0 into the found equation, we get:
y (0) = 2 ln (3) - 1 + ln (3) + C * 1 + C * 2 = 3 ln (3) - 1 + C * 1 + C * 2 = 1 + 3ln3
Find the first derivative of the resulting general solution:
y ’= 2e 2x (2C 1 e 2x + C 2 -2x +4 e 2x ln (e -2x +2) + ln (2e 2x +1) -2)
Substituting x = 0, we get:
y ’(0) = 2 (2C 1 + C 2 +4 ln (3) + ln (3) -2) = 4C 1 + 2C 2 +10 ln (3) -4 = 10ln3
We get a system of two equations:
3 ln (3) - 1 + C * 1 + C * 2 = 1 + 3ln3
4C 1 + 2C 2 +10 ln (3) -4 = 10ln3
or
C * 1 + C * 2 = 2
4C 1 + 2C 2 = 4
or
C * 1 + C * 2 = 2
2C 1 + C 2 = 2
From where: C 1 = 0, C * 2 = 2
A private solution will be written as:
y = 2e 4x ln (e -2x +2) - e 2x + e 2x ln (2e 2x +1) - 2x e 2x + 2 e 2x
Variation method of arbitrary constants
The method of variation of arbitrary constants for constructing a solution to a linear inhomogeneous differential equation
a n (t)z (n) (t) + a n − 1 (t)z (n − 1) (t) + ... + a 1 (t)z"(t) + a 0 (t)z(t) = f(t)
consists in replacing arbitrary constants c k in general solution
z(t) = c 1 z 1 (t) + c 2 z 2 (t) + ... + c n z n (t)
corresponding homogeneous equation
a n (t)z (n) (t) + a n − 1 (t)z (n − 1) (t) + ... + a 1 (t)z"(t) + a 0 (t)z(t) = 0
to auxiliary functions c k (t) whose derivatives satisfy the linear algebraic system
The determinant of system (1) is the Wronskian of the functions z 1 ,z 2 ,...,z n , which ensures its unique decidability with respect to.
If are antiderivatives for, taken at fixed values of the integration constants, then the function
is a solution to the original linear inhomogeneous differential equation. Integration of an inhomogeneous equation in the presence of a general solution to the corresponding homogeneous equation is thus reduced to quadratures.
Variation method for arbitrary constants for constructing solutions of a system of linear differential equations in vector normal form
consists in constructing a particular solution (1) in the form
where Z(t) is the basis of solutions of the corresponding homogeneous equation, written in the form of a matrix, and the vector function that replaced the vector of arbitrary constants is defined by the relation. The desired particular solution (with zero initial values at t = t 0 has the form

For a system with constant coefficients, the last expression is simplified:

Matrix Z(t)Z- 1 (τ) called the Cauchy matrix operator L = A(t) .