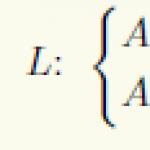It has many applications, since it allows an approximate representation of a given function by other simpler ones. OLS can be extremely useful in processing observations, and it is actively used to estimate some quantities from the results of measurements of others that contain random errors. This article will show you how to implement least squares calculations in Excel.

Statement of the problem using a specific example

Suppose there are two indicators X and Y. And Y depends on X. Since OLS is of interest to us from the point of view of regression analysis (in Excel, its methods are implemented using built-in functions), then you should immediately go on to consider a specific problem.

So, let X be the retail space of a grocery store, measured in square meters, and Y - the annual turnover, measured in millions of rubles.

It is required to make a forecast of what turnover (Y) the store will have if it has a particular retail space. Obviously, the function Y = f (X) is increasing, since the hypermarket sells more goods than the stall.

A few words about the correctness of the initial data used for prediction

Let's say we have a table built from data for n stores.

According to mathematical statistics, the results will be more or less correct if data on at least 5-6 objects are examined. In addition, you cannot use "abnormal" results. In particular, an elite small boutique can have a turnover many times greater than the turnover of large retail outlets of the "masmarket" class.

Method essence

The table data can be displayed on the Cartesian plane as points M 1 (x 1, y 1),… M n (x n, y n). Now the solution of the problem will be reduced to the selection of an approximating function y = f (x) with a graph passing as close as possible to the points M 1, M 2, .. M n.

Of course, you can use a high degree polynomial, but this option is not only difficult to implement, but also simply incorrect, since it will not reflect the main trend that needs to be detected. The most reasonable solution is to find the straight line y = ax + b, which best approximates the experimental data, or rather, the coefficients - a and b.

Accuracy assessment

For any approximation, an assessment of its accuracy is of particular importance. Let us denote by e i the difference (deviation) between the functional and experimental values for the point x i, that is, e i = y i - f (x i).

Obviously, to estimate the accuracy of the approximation, the sum of deviations can be used, i.e., when choosing a straight line for an approximate representation of the dependence of X on Y, one should give preference to the one with the smallest value of the sum e i at all points under consideration. However, not everything is so simple, since along with positive deviations, negative deviations will practically be present.

The problem can be solved using the modules of deviations or their squares. The last method is the most widely used. It is used in many areas, including regression analysis (Excel implements two built-in functions), and has long proven its worth.

Least square method

In Excel, as you know, there is a built-in autosum function that allows you to calculate the values of all values located in the selected range. Thus, nothing prevents us from calculating the value of the expression (e 1 2 + e 2 2 + e 3 2 + ... e n 2).

In mathematical notation, it looks like:

Since the decision was initially made to approximate using a straight line, we have:

Thus, the problem of finding the straight line that best describes the specific dependence of the quantities X and Y is reduced to calculating the minimum of a function of two variables:

This requires equating to zero the partial derivatives with respect to the new variables a and b, and solving a primitive system consisting of two equations with 2 unknowns of the form:

After some simple transformations, including dividing by 2 and manipulating the sums, we get:

Solving it, for example, by Cramer's method, we obtain a stationary point with some coefficients a * and b *. This is the minimum, that is, to predict what turnover the store will have for a certain area, the straight line y = a * x + b * is suitable, which is a regression model for the example in question. Of course, it will not allow you to find the exact result, but it will help you get an idea of whether the purchase on credit for a store of a particular area will pay off.

How to implement least squares method in Excel

Excel has a function for calculating the OLS value. It has the following form: "TREND" (known Y values; known X values; new X values; const.). Let's apply the formula for calculating the OLS in Excel to our table.

To do this, in the cell in which the result of the calculation by the least squares method in Excel should be displayed, enter the "=" sign and select the "TREND" function. In the window that opens, fill in the appropriate fields, highlighting:

the range of known values for Y (in this case, data for turnover);
range x 1,… x n, ie the size of the retail space;
both known and unknown values of x, for which you need to find out the size of the turnover (see below for information on their location on the worksheet).

In addition, the formula contains the Boolean variable "Const". If you enter 1 in the corresponding field, this will mean that calculations should be performed, assuming that b = 0.

If you need to know the forecast for more than one value of x, then after entering the formula, you should not press "Enter", but you need to type on the keyboard the combination "Shift" + "Control" + "Enter" ("Enter").

Some features

Regression analysis may even be available to dummies. The Excel formula for predicting the value of an array of unknown variables - "TREND" - can be used even by those who have never heard of the method of least squares. It is enough just to know some of the features of her work. In particular:

If you arrange the range of known values of the y variable in one row or column, then each row (column) with known x values will be perceived by the program as a separate variable.
If the "TREND" window does not contain a range with known x, then if the function is used in Excel, the program will consider it as an array consisting of integers, the number of which corresponds to the range with the given values of the y variable.
To get an array of “predicted” values as an output, the trend expression must be entered as an array formula.
If new x values are not specified, then the TREND function considers them to be equal to known. If they are not specified, then array 1 is taken as an argument; 2; 3; 4;…, which is commensurate with the range with the already given parameters y.
The range containing the new x-values must be the same or more rows or columns as the range with the given y-values. In other words, it should be commensurate with the independent variables.
An array with known x values can contain multiple variables. However, if we are talking only about one, then it is required that the ranges with the given values of x and y are commensurate. In the case of multiple variables, you want the range with the given y values to fit in one column or one row.

FORECAST function

It is implemented with several functions. One of them is called "FORECAST". It is similar to "TREND", that is, it gives the result of calculations using the least squares method. However, only for one X, for which the Y value is unknown.

Now you know the formulas in Excel for dummies that allow you to predict the future value of a given indicator according to a linear trend.

Well, at work they reported to the inspection, the article was written at home for the conference - now you can write to the blog. While I was processing my data, I realized that I could not help but write about a very cool and necessary add-in in Excel, which is called. So the article will be devoted to this particular add-in, and I will tell you about it using an example of use least squares method(OLS) to search for unknown equation coefficients when describing experimental data.

How to enable the Find Solution add-in

First, let's figure out how to enable this add-in.

1. Go to the "File" menu and select "Excel Options"

2. In the window that appears, select "Search for a solution" and click "go".

3. In the next window, put a tick in front of the item "search for a solution" and click "OK".

4. The add-on is activated - now it can be found in the "Data" menu item.

Least square method

Now briefly about least squares method (OLS) and where it can be applied.

Let's say we have a dataset after we did some experiment where we studied the effect of the X value on the Y value.

We want to describe this influence mathematically, so that later we can use this formula and know that if we change the value of X by so much, we get the value of Y so and so ...

I'll take a super-simple example (see fig.).

It’s clear that the points are located one after the other as if in a straight line, and therefore we safely assume that our dependence is described by a linear function y = kx + b. At the same time, we are definitely sure that when X is equal to zero, the value of Y is also equal to zero. This means that the function describing the dependence will be even simpler: y = kx (remember the school curriculum).

In general, we have to find the coefficient k. This is what we will do with OLS using the "search for a solution" add-in.

The method consists in the fact that (here - attention: you need to think about it) the sum of the squares of the differences between the experimentally obtained and the corresponding calculated values was minimal. That is, when X1 = 1 the actually measured value Y1 = 4.6, and the calculated y1 = f (x1) is 4, the square of the difference will be (y1-Y1) ^ 2 = (4-4.6) ^ 2 = 0.36 ... With the following the same: when X2 = 2, the actually measured value Y2 = 8.1, and the calculated y2 is 8, the square of the difference will be (y2-Y2) ^ 2 = (8-8.1) ^ 2 = 0.01. And the sum of all these squares should be as small as possible.

So, let's start training on using the OLS and Find Solution Excel Add-ins .

Applying the solution search add-in

1. If you have not turned on the "search for a solution" add-on, then go back to point How to enable the search for a solution add-in and enable 🙂

2. In cell A1, enter the value "1". This unit will be the first approximation to the real value of the coefficient (k) of our functional dependence y = kx.

3. In column B, we have the values of the X parameter, in column C - the values of the Y parameter. In the cells of the D column, we enter the formula: "coefficient k multiplied by the value of X". For example, in cell D1 we enter "= A1 * B1", in cell D2 we enter "= A1 * B2", and so on.

4. We believe that the coefficient k is equal to one and the function f (x) = y = 1 * x is the first approximation to our solution. We can calculate the sum of the squares of the differences between the measured values of Y and those calculated by the formula y = 1 * x. We can do all this manually by driving in the appropriate cell references into the formula: "= (D2-C2) ^ 2 + (D3-C3) ^ 2 + (D4-C4) ^ 2 ... etc. Finally we are mistaken and understand that we have lost a lot of time. In Excel, for calculating the sum of squares of differences, there is a special formula, "SUMKVRAZN", which will do everything for us. Enter it in cell A2 and set the initial data: the range of measured values Y (column C) and the range of calculated Y values (column D).

4. The sum of the differences of the squares has been calculated - now we go to the “Data” tab and select “Search for a solution”.

5. In the menu that appears, select cell A1 (the one with the coefficient k) as the cell to be changed.

6. Select cell A2 as the target and set the condition “set equal to the minimum value”. Remember that this is the cell where we calculate the sum of the squares of the differences between the calculated and measured values, and this sum should be minimal. Click "execute".

7. Coefficient k is selected. Now you can verify that the calculated values are now very close to the measured ones.

P.S.

In general, of course, to approximate experimental data in Excel, there are special tools that allow you to describe data using a linear, exponential, power and polynomial function, so you can often do without n solution search add-ons... I talked about all these approximation methods in my mine, so if you're interested, take a look. But when it comes to some exotic function with one unknown coefficient or optimization problems, here superstructure very opportunely.

Find solution add-in can be used for other tasks, the main thing is to understand the essence: there is a cell where we select a value, and there is a target cell in which a condition is set for selecting an unknown parameter.
That's all! In the next article I will tell you a fairy tale about a vacation, so in order not to miss the article,

Least square method is used to estimate the parameters of the regression equation.

One of the methods for studying stochastic relationships between features is regression analysis.
Regression analysis is the derivation of the regression equation, with the help of which the average value of a random variable (feature-result) is found, if the value of another (or other) variables (feature-factors) is known. It includes the following steps:

choice of the form of communication (type of analytical regression equation);
estimation of the parameters of the equation;
assessment of the quality of the analytical regression equation.

Most often, a linear form is used to describe the statistical relationship of features. Attention to the linear relationship is explained by a clear economic interpretation of its parameters, limited variation of variables and the fact that in most cases nonlinear forms of communication for performing calculations are converted (by logarithm or change of variables) into a linear form.
In the case of a linear pairwise relationship, the regression equation will take the form: y i = a + b x i + u i. The parameters of this equation a and b are estimated from the data of statistical observation x and y. The result of such an assessment is the equation:, where, are the estimates of the parameters a and b, is the value of the effective attribute (variable) obtained by the regression equation (calculated value).

The most often used to estimate parameters least squares method (OLS).
The least squares method gives the best (consistent, efficient and unbiased) estimates of the parameters of the regression equation. But only if certain prerequisites are met regarding the random term (u) and the independent variable (x) (see OLS prerequisites).

The problem of estimating the parameters of a linear paired equation by the least squares method consists in the following: to obtain such parameter estimates, at which the sum of the squares of the deviations of the actual values of the effective indicator - y i from the calculated values - is minimal.
Formally OLS criterion can be written like this: .

Least squares classification

Least square method.
Maximum likelihood method (for the normal classical linear regression model, the normality of the regression residuals is postulated).
The generalized least squares OLS method is used in the case of autocorrelation of errors and in the case of heteroscedasticity.
Weighted least squares method (a special case of OLS with heteroscedastic residuals).

Let's illustrate the essence the classical least squares method graphically... To do this, we will build a dot plot according to the observation data (x i, y i, i = 1; n) in a rectangular coordinate system (such a dot plot is called the correlation field). Let's try to find a straight line that is closest to the points of the correlation field. According to the method of least squares, the line is chosen so that the sum of the squares of the vertical distances between the points of the correlation field and this line would be minimal.

Mathematical record of this problem: .
We know the values of y i and x i = 1 ... n, these are observational data. In the S function, they are constants. The variables in this function are the required parameter estimates -,. To find the minimum of a function of 2 variables, it is necessary to calculate the partial derivatives of this function with respect to each of the parameters and equate them to zero, i.e. .
As a result, we get a system of 2 normal linear equations:
Solving this system, we find the required parameter estimates:

The correctness of the calculation of the parameters of the regression equation can be checked by comparing the sums (there may be some discrepancy due to rounding of calculations).
To calculate the parameter estimates, you can build table 1.
The sign of the regression coefficient b indicates the direction of the relationship (if b> 0, the relationship is direct, if b<0, то связь обратная). Величина b показывает на сколько единиц изменится в среднем признак-результат -y при изменении признака-фактора - х на 1 единицу своего измерения.
Formally, the value of parameter a is the average value of y at x equal to zero. If the attribute factor does not and cannot have a zero value, then the above interpretation of the parameter a does not make sense.

Assessment of the tightness of the relationship between the signs is carried out using the coefficient of linear pair correlation - r x, y. It can be calculated using the formula: ... In addition, the linear pairwise correlation coefficient can be determined through the regression coefficient b: .
The range of admissible values of the linear pair correlation coefficient is from –1 to +1. The sign of the correlation coefficient indicates the direction of the link. If r x, y> 0, then the connection is direct; if r x, y<0, то связь обратная.
If this coefficient is close to one in absolute value, then the relationship between the features can be interpreted as a rather close linear one. If its modulus is equal to one ê r x, y ê = 1, then the connection between the features is functional linear. If features x and y are linearly independent, then r x, y is close to 0.
To calculate r x, y, you can also use table 1.

To assess the quality of the obtained regression equation, the theoretical coefficient of determination is calculated - R 2 yx:

,
where d 2 is the variance y explained by the regression equation;
e 2 - residual (not explained by the regression equation) variance y;
s 2 y is the total (total) variance of y.
The coefficient of determination characterizes the proportion of the variation (variance) of the effective trait y, explained by the regression (and, consequently, the factor x), in the total variation (variance) y. The coefficient of determination R 2 yx takes values from 0 to 1. Accordingly, the value 1-R 2 yx characterizes the proportion of variance y caused by the influence of other factors not taken into account in the model and specification errors.
With paired linear regression R 2 yx = r 2 yx.

Least squares method (OLS)

The system of m linear equations with n unknowns has the form:

Three cases are possible: m n. The case when m = n was considered in the previous sections. For m

If m> n and the system is consistent, then the matrix A has at least m - n linearly dependent rows. Here the solution can be obtained by selecting any n linearly independent equations (if they exist) and applying the formula X = A -1 CHV, that is, by reducing the problem to the previously solved one. In this case, the obtained solution will always satisfy the rest of the m - n equations.

However, when using a computer, it is more convenient to use a more general approach - the method of least squares.

Algebraic least squares

The algebraic least squares method is understood as a method for solving systems of linear equations

by minimizing the Euclidean norm

Ax? b? > inf. (1.2)

Experiment data analysis

Consider some experiment, during which at the moments of time

the temperature Q (t) is measured, for example. Let the measurement results be given by the array

Let us assume that the conditions of the experiment are such that the measurements are carried out with a deliberate error. In these cases, the law of temperature variation Q (t) is sought using some polynomial

P (t) = + + + ... +,

determining the unknown coefficients, ..., from the considerations that the value E (, ...,), defined by the equality

gauss algebraic exel approximation

took the minimum value. Since the sum of squares is minimized, this method is called least squares data fit.

If we replace P (t) by its expression, then we get

Let us pose the problem of defining an array so that the value is minimal, i.e. Let's define an array using the least squares method. To do this, we equate the partial derivatives to zero:

If you enter m × n matrix A = (), i = 1, 2 ..., m; j = 1, 2, ..., n, where

I = 1, 2 ..., m; j = 1, 2, ..., n,

then the written equality takes the form

Let us rewrite the written equality in terms of operations with matrices. We have by definition of matrix-column multiplication

For a transposed matrix, a similar relationship looks like this

Let us introduce the notation: the i-th component of the vector Ax will be denoted.In accordance with the written matrix equalities, we will have

In matrix form, this equality can be rewritten as

A T x = A T B (1.3)

Here A is a rectangular m × n matrix. Moreover, in problems of data approximation, as a rule, m> n. Equation (1.3) is called the normal equation.

It was possible from the very beginning, using the Euclidean norm of vectors, to write the problem in an equivalent matrix form:

Our goal is to minimize this function with respect to x. In order for the minimum to be reached at the solution point, the first derivatives with respect to x at this point must equal zero. The derivatives of this function are

2A T B + 2A T Ax

and therefore the solution must satisfy the system of linear equations

(A T A) x = (A T B).

These equations are called normal equations. If A is an m × n matrix, then A> A - n × n is a matrix, i.e. the matrix of the normal equation is always a quadratic symmetric matrix. Moreover, it possesses the property of positive definiteness in the sense that (A> Ax, x) = (Ax, Ax)? 0.

Comment. Sometimes the solution of an equation of the form (1.3) is called the solution of the system Ax = B, where A is a rectangular m × n (m> n) matrix by the least squares method.

The least squares problem can be graphically interpreted as minimizing the vertical distances from the data points to the model curve (see Figure 1.1). This idea is based on the assumption that all the errors in the approximation correspond to the errors in the observations. If there are also errors in the explanatory variables, then it may be more appropriate to minimize the Euclidean distance from the data to the model.

OLS to Excel

The algorithm for implementing the OLS in Excel below assumes that all the initial data are already known. Both sides of the matrix equation AЧX = B of the system are multiplied on the left by the transposed matrix of the system AT:

AT AX = AT B

Then we multiply both sides of the equation on the left by the matrix (AT A) -1. If this matrix exists, then the system is defined. Considering that

(AT A) -1 * (AT A) = E, we get

X = (AT A) -1 AT B.

The resulting matrix equation is a solution to a system of m linear equations with n unknowns for m> n.

Let's consider the application of the above algorithm for a specific example.

Example. Let it be necessary to solve the system

In Excel, the list with the solution in the formulas display mode for this task looks like this:

Calculation results:

The required vector X is located in the range E11: E12.

When solving a given system of linear equations, the following functions were used:

1. MOBRE - Returns the inverse of a matrix stored in an array.

Syntax: MOBR (array).

Array - A numeric array with an equal number of rows and columns.

2. MULTIPLE - returns the product of matrices (matrices are stored in arrays). The result is an array with the same number of rows as array1 and the same number of columns as array2.

Syntax: MULTIPLE (array1, array2).

Array1, array2 - multiplied arrays.

After entering the function in the upper left cell of the array range, select the array starting with the cell containing the formula, press F2, and then press CTRL + SHIFT + ENTER.

3. TRANSPOSE - converts a vertical set of cells to a horizontal one, or vice versa. The result of using this function is an array with the number of rows equal to the number of columns in the original array and the number of columns equal to the number of rows in the initial array.

Least squares is a mathematical procedure for constructing a linear equation that most closely matches a set of two series of numbers. The purpose of this method is to minimize the total squared error. Excel has tools that you can use to apply this method in calculations. Let's see how this is done.

Using the method in Excel

o Enabling the Solver Add-in

o Problem conditions

o Decision

Using the method in Excel

The method of least squares (OLS) is a mathematical description of the dependence of one variable on the other. It can be used in forecasting.

Enabling the Solver add-in

In order to use OLS in Excel, you need to enable the add-in "Search for a solution" which is disabled by default.

1. Go to the tab "File".

2. Click on the name of the section "Options".

3. In the window that opens, stop the selection on the subsection "Add-ons".

4. In the block "Control" located at the bottom of the window, set the switch to the position Excel Add-ins(if it has a different value) and click on the button "Go ...".

5. A small window opens. We put a tick next to the parameter in it "Search for a solution"... Click on the button "OK".

Now the function Finding a solution in Excel is activated, and its tools have appeared on the ribbon.

Lesson: Finding a solution in Excel

Conditions of the problem

Let us describe the application of the OLS with a specific example. We have two rows of numbers x and y, the sequence of which is shown in the image below.

The function can most accurately describe this dependence:

Moreover, it is known that for x = 0 y is also equal 0 ... Therefore, this equation can be described by the dependence y = nx.

We have to find the minimum sum of the squares of the difference.

Solution

Let's move on to describing the direct application of the method.

1. To the left of the first value x put a number 1 ... This will be the approximate value of the first value of the coefficient n.

2. To the right of the column y add one more column - nx... In the first cell of this column, write the formula for multiplying the coefficient n per cell of the first variable x... At the same time, we make the link to the field with the coefficient absolute, since this value will not change. Click on the button Enter.

3. Using a fill handle, copy this formula to the entire table range in the column below.

4. In a separate cell, calculate the sum of the differences of the squares of the values y and nx... To do this, click on the button "Insert function".

5. In the opened "Function Wizard" looking for a record "SUMKVRAZN"... Select it and click on the button "OK".

6. The arguments window opens. In field "Array_x" y... In field "Array_y" we enter the range of cells of the column nx... In order to enter values, simply place the cursor in the field and select the corresponding range on the sheet. After entering, click on the button "OK".

7. Go to the tab "Data"... On the ribbon in the toolbox "Analysis" push the button "Search for a solution".

8. The parameters window for this tool is opened. In field "Optimize target function" we indicate the address of the cell with the formula "SUMKVRAZN"... In the parameter "Before" be sure to set the switch to the position "Minimum"... In field "Changing cells" specify the address with the value of the coefficient n... Click on the button "Find a solution".

9. The solution will be displayed in the cell of the coefficient n... It is this value that will be the least square of the function. If the result satisfies the user, then press the button "OK" in an additional window.

As you can see, the application of the least squares method is a rather complicated mathematical procedure. We have shown it in action using the simplest example, but there are much more complex cases. However, the Microsoft Excel toolkit is designed to simplify the calculations as much as possible.

http://multitest.semico.ru/mnk.htm

General Provisions

The smaller the number in absolute value, the better the straight line (2) is selected. As a characteristic of the accuracy of the selection of straight line (2), we can take the sum of squares

The minimum conditions for S will be

	(6)
	(7)

Equations (6) and (7) can be written as follows:

	(8)
	(9)

From equations (8) and (9) it is easy to find a and b from the experimental values x i and y i. Line (2), defined by equations (8) and (9), is called the line obtained by the method of least squares (this name emphasizes that the sum of squares S has a minimum). Equations (8) and (9), from which the straight line (2) is determined, are called normal equations.

You can indicate a simple and general way of writing normal equations. Using the experimental points (1) and equation (2), we can write the system of equations for a and b

y 1 = ax 1 + b,
y 2 = ax 2 + b, ...		(10)
y n = ax n + b,

We multiply the left and right sides of each of these equations by the coefficient of the first unknown a (i.e., by x 1, x 2, ..., x n) and add the resulting equations, the result is the first normal equation (8).

We multiply the left and right sides of each of these equations by the coefficient of the second unknown b, i.e. by 1, and add the resulting equations, the result is the second normal equation (9).

This method of obtaining normal equations is general: it is suitable, for example, for the function

there is a constant value and it must be determined from experimental data (1).

The system of equations for k can be written:

Find line (2) using the least squares method.

Solution. We find:

X i = 21, y i = 46.3, x i 2 = 91, x i y i = 179.1.

We write down equations (8) and (9) 91a + 21b = 179.1,

21a + 6b = 46.3, hence we find
a = 0.98 b = 4.3.