Continuiamo a occuparci di sistemi di equazioni lineari. Finora, abbiamo esaminato i sistemi che hanno un'unica soluzione. Tali sistemi possono essere risolti in qualsiasi modo: metodo di sostituzione("Scuola"), dalle formule di Cramer, metodo matriciale, metodo gaussiano... Tuttavia, in pratica, sono diffusi altri due casi quando:
1) il sistema è incompatibile (non ha soluzioni);
2) il sistema ha infinite soluzioni.
Per questi sistemi, viene utilizzato il più universale di tutti i metodi di soluzione: Metodo di Gauss... In effetti, il metodo "scuola" porterà alla risposta, ma nella matematica superiore è consuetudine utilizzare il metodo gaussiano dell'eliminazione successiva delle incognite. Per coloro che non hanno familiarità con l'algoritmo del metodo gaussiano, si prega di studiare prima la lezione Metodo di Gauss
Le stesse trasformazioni della matrice elementare sono esattamente le stesse, la differenza sarà alla fine della soluzione. Consideriamo prima un paio di esempi quando il sistema non ha soluzioni (incoerente).
Esempio 1
Cosa salta subito all'occhio in questo sistema? Il numero di equazioni è minore del numero di variabili. Esiste un teorema che afferma: "Se il numero di equazioni nel sistema è inferiore al numero di variabili, allora il sistema o è inconsistente o ha infinite soluzioni." E resta solo da scoprire.
L'inizio della soluzione è completamente ordinario: scriviamo la matrice estesa del sistema e, usando trasformazioni elementari, la portiamo in una forma graduale:
(1). Nel passaggio in alto a sinistra, dobbiamo ottenere (+1) o (–1). Non ci sono tali numeri nella prima colonna, quindi riorganizzare le righe non darà nulla. L'unità dovrà essere organizzata in modo indipendente e ciò può essere fatto in diversi modi. Abbiamo fatto questo. Alla prima riga aggiungi la terza riga moltiplicata per (–1).
(2). Ora otteniamo due zeri nella prima colonna. Alla seconda riga aggiungiamo la prima riga moltiplicata per 3. Alla terza riga aggiungiamo la prima riga moltiplicata per 5.
(3). Dopo la trasformazione eseguita, è sempre consigliabile guardare ed è possibile semplificare le linee risultanti? Può. Dividi la seconda riga per 2, ottenendo allo stesso tempo il (–1) desiderato sul secondo gradino. Dividi la terza riga per (–3).
(4). Aggiungi la seconda riga alla terza riga. Probabilmente tutti hanno prestato attenzione alla cattiva linea che si è rivelata a seguito di trasformazioni elementari:
... È chiaro che non può essere così.
Infatti, riscriviamo la matrice risultante
tornando al sistema di equazioni lineari:
Se, a seguito di trasformazioni elementari, una stringa della forma , doveλ - un numero diverso da zero, quindi il sistema è incompatibile (non ha soluzioni).
Come faccio a registrare la fine di un compito? Devi scrivere la frase:
“Come risultato di trasformazioni elementari, si ottenne una stringa della forma, dove λ ≠ 0 ". Risposta: "Il sistema non ha soluzioni (incoerente)."
Si prega di notare che in questo caso non c'è il backtracking dell'algoritmo gaussiano, non ci sono soluzioni e semplicemente non c'è nulla da trovare.
Esempio 2
Risolvi un sistema di equazioni lineari 
Questo è un esempio di soluzione fai-da-te. Soluzione completa e risposta alla fine del tutorial.
Ancora una volta, ti ricordiamo che il tuo corso decisionale può differire dal nostro corso decisionale, il metodo di Gauss non specifica un algoritmo univoco, devi indovinare l'ordine delle azioni e le azioni stesse in ogni caso in modo indipendente.
Un'altra caratteristica tecnica della soluzione: le trasformazioni elementari possono essere fermate subito, non appena è apparsa una riga della forma, dove λ ≠ 0 ... Considera un esempio condizionale: supponiamo che dopo la primissima trasformazione si ottenga la matrice
.
Questa matrice non è stata ancora ridotta a una forma a gradini, ma non sono necessarie ulteriori trasformazioni elementari, poiché è apparsa una linea della forma, dove λ ≠ 0 ... Dovresti rispondere immediatamente che il sistema è incompatibile.
Quando un sistema di equazioni lineari non ha soluzioni, questo è quasi un regalo per lo studente, poiché si ottiene una soluzione breve, a volte letteralmente in 2-3 passaggi. Ma tutto in questo mondo è equilibrato, e il problema in cui il sistema ha infinite soluzioni è solo più lungo.
Esempio 3:
Risolvi un sistema di equazioni lineari
Ci sono 4 equazioni e 4 incognite, quindi il sistema può avere un'unica soluzione, o non avere soluzioni, o avere infinite soluzioni. Comunque sia, ma il metodo di Gauss ci porterà comunque alla risposta. Questa è la sua versatilità.
L'inizio è di nuovo standard. Scriviamo la matrice estesa del sistema e, usando trasformazioni elementari, portiamola in una forma graduale:
Questo è tutto, e tu avevi paura.
(1). Si prega di notare che tutti i numeri nella prima colonna sono divisibili per 2, quindi siamo soddisfatti di due sul gradino in alto a sinistra. Alla seconda riga aggiungi la prima riga moltiplicata per (–4). Alla terza riga aggiungi la prima riga moltiplicata per (–2). Alla quarta riga aggiungi la prima riga moltiplicata per (–1).
Attenzione! Molti possono essere tentati dalla quarta riga sottrarre prima linea. Questo può essere fatto, ma non è necessario, l'esperienza mostra che la probabilità di un errore nei calcoli aumenta più volte. Basta aggiungere: alla quarta riga aggiungere la prima riga moltiplicata per (–1) - Esattamente!
(2). Le ultime tre righe sono proporzionali, due di esse possono essere eliminate. Anche qui devi mostrare maggiore attenzione, ma le linee sono davvero proporzionali? Per sicurezza, non sarà superfluo moltiplicare la seconda riga per (–1) e dividere la quarta riga per 2, ottenendo tre righe identiche. E solo allora cancellane due. Come risultato di trasformazioni elementari, la matrice espansa del sistema è ridotta a una forma graduale:
Quando si compila un'attività su un quaderno, è consigliabile scrivere le stesse note a matita per chiarezza.
Riscriviamo il corrispondente sistema di equazioni: 
Non puzza come una "solita" unica soluzione del sistema. Una brutta linea dove λ ≠ 0, anche no. Ciò significa che questo è il terzo caso rimanente: il sistema ha infinite soluzioni.
Le infinite soluzioni del sistema si scrivono brevemente nella forma del cosiddetto soluzione di sistema globale.
Troviamo la soluzione generale del sistema usando l'andamento inverso del metodo di Gauss. Per i sistemi di equazioni con un insieme infinito di soluzioni, compaiono nuovi concetti: "Variabili di base" e "Variabili libere"... Per prima cosa, definiamo quali variabili abbiamo di base, e quali variabili - gratuito... Non è necessario spiegare in dettaglio i termini dell'algebra lineare, è sufficiente ricordare che esistono tali variabili di base e variabili libere.
Le variabili di base "siedono" sempre rigorosamente sui gradini della matrice... In questo esempio, le variabili di base sono X 1 e X 3 .
Le variabili libere sono tutto rimanente variabili che non hanno ricevuto un gradino. Nel nostro caso ce ne sono due: X 2 e X 4 - variabili libere.
Ora hai bisogno Tuttivariabili di base esprimere solo attraversovariabili libere... Il contrario dell'algoritmo gaussiano funziona tradizionalmente dal basso verso l'alto. Dalla seconda equazione del sistema, esprimiamo la variabile base X 3:
Vediamo ora la prima equazione: 
... Innanzitutto, sostituiamo l'espressione trovata in essa:
Resta da esprimere la variabile di base X 1 tramite variabili libere X 2 e X 4:
Alla fine, abbiamo ottenuto ciò di cui abbiamo bisogno - Tutti variabili di base ( X 1 e X 3) espresso solo attraverso variabili libere ( X 2 e X 4):
In realtà, la soluzione generale è pronta:
.
Come scrivere correttamente la soluzione generale? Prima di tutto, le variabili libere sono scritte nella soluzione generale "da sole" e rigorosamente al loro posto. In questo caso, variabili libere X 2 e X 4 va scritto in seconda e quarta posizione:
.
Le espressioni ottenute per le variabili di base e, ovviamente, devi scrivere in prima e terza posizione:
Dalla soluzione generale del sistema se ne trovano infiniti soluzioni private... È molto semplice. Variabili libere X 2 e X 4 si chiamano così perché si possono dare qualsiasi valore finale... I valori più popolari sono zero, perché questa è la soluzione più semplice per la soluzione particolare.
Sostituzione ( X 2 = 0; X 4 = 0) nella soluzione generale, si ottiene una delle soluzioni particolari:
, oppure è una soluzione particolare corrispondente a variabili libere a valori ( X 2 = 0; X 4 = 0).
Le unità sono un'altra dolce coppia, sostitutiva ( X 2 = 1 e X 4 = 1) in una soluzione generale:
, cioè (-1; 1; 1; 1) è un'altra soluzione particolare.
È facile vedere che il sistema di equazioni ha infinite soluzioni, poiché possiamo dare variabili libere qualunque valori.
Ogni la particolare soluzione deve soddisfare a ogni equazione del sistema. Questa è la base per il controllo "rapido" della correttezza della soluzione. Prendi, ad esempio, una soluzione particolare (-1; 1; 1; 1) e sostituiscila nella parte sinistra di ciascuna equazione del sistema originale:
Tutto dovrebbe combaciare. E con qualsiasi decisione particolare che ricevi, anche tutto dovrebbe essere d'accordo.
A rigor di termini, il controllo di una particolare soluzione a volte inganna, ad es. qualche soluzione particolare può soddisfare ogni equazione del sistema, ma la soluzione generale stessa viene effettivamente trovata in modo errato. Pertanto, prima di tutto, il controllo della soluzione generale è più approfondito e affidabile.
Come verificare la soluzione generale risultante 
?
Non è difficile, ma richiede molte trasformazioni che richiedono tempo. Devi prendere espressioni di base variabili, in questo caso 
e, e sostituirli nella parte sinistra di ogni equazione del sistema.
A sinistra della prima equazione del sistema:
Si ottiene il membro destro della prima equazione iniziale del sistema.
A sinistra della seconda equazione del sistema:
Si ottiene il membro destro della seconda equazione originale del sistema.
E inoltre - ai lati sinistro della terza e quarta equazione del sistema. Questo controllo richiede più tempo, ma garantisce la correttezza al cento per cento della soluzione complessiva. Inoltre, in alcune attività, è proprio la verifica della soluzione generale che è richiesta.
Esempio 4:
Risolvi il sistema con il metodo gaussiano. Trova una soluzione generale e due particolari. Controlla la soluzione generale.
Questo è un esempio di soluzione fai-da-te. Qui, a proposito, ancora una volta il numero di equazioni è inferiore al numero di incognite, il che significa che è immediatamente chiaro che il sistema sarà o incompatibile o con un insieme infinito di soluzioni.
Esempio 5:
Risolvi un sistema di equazioni lineari. Se il sistema ha infinite soluzioni, trova due soluzioni particolari e verifica la soluzione generale
Soluzione: Scriviamo la matrice estesa del sistema e, usando trasformazioni elementari, portiamola in una forma graduale:
(1). Aggiungi la prima riga alla seconda riga. Alla terza riga aggiungiamo la prima riga moltiplicata per 2. Alla quarta riga aggiungiamo la prima riga moltiplicata per 3.
(2). Alla terza riga, aggiungi la seconda riga moltiplicata per (–5). Alla quarta riga, aggiungi la seconda riga moltiplicata per (–7).
(3). La terza e la quarta riga sono uguali, ne eliminiamo una. Ecco tanta bellezza:
Le variabili di base siedono su pioli, quindi variabili di base.
C'è solo una variabile libera che non ha ottenuto un passaggio qui:.
(4). Movimento inverso. Esprimiamo le variabili di base in termini di variabile libera:
Dalla terza equazione:
Considera la seconda equazione e sostituiscici l'espressione trovata:
, 
, ,
Considera la prima equazione e sostituisci le espressioni trovate e in essa:
Quindi, la soluzione generale per una variabile libera è X 4:
Ancora una volta, come è successo? Variabile libera X 4 siede da solo nel suo legittimo quarto posto. Anche le espressioni risultanti per le variabili di base sono al loro posto.
Verifichiamo subito la soluzione generale.
Sostituiamo le variabili di base, nella parte sinistra di ogni equazione del sistema:
Si ottengono i corrispondenti membri destri delle equazioni, quindi si trova la corretta soluzione generale.
Ora dalla soluzione comune trovata 
otteniamo due soluzioni particolari. Tutte le variabili sono espresse qui attraverso un singolo variabile libera x 4 . Non hai bisogno di scervellarti.
lascia stare X 4 = 0, quindi 
- la prima soluzione particolare.
lascia stare X 4 = 1, quindi 
- una soluzione più particolare.
Risposta: Decisione comune: ... Soluzioni private:
e .
Esempio 6:
Trova la soluzione generale di un sistema di equazioni lineari.
Abbiamo già verificato la decisione generale, la risposta può essere attendibile. Il tuo corso di decisione può differire dal nostro corso di decisione. La cosa principale è che le decisioni comuni coincidano. Probabilmente, molti hanno notato un momento spiacevole nelle soluzioni: molto spesso, durante il corso inverso del metodo di Gauss, abbiamo dovuto armeggiare con frazioni ordinarie... In pratica, questo è vero, i casi in cui non ci sono frazioni sono molto meno comuni. Preparati mentalmente e, soprattutto, tecnicamente.
Soffermiamoci sulle caratteristiche della soluzione che non sono state trovate negli esempi risolti. La soluzione generale del sistema può talvolta includere una costante (o costanti).
Ad esempio, la soluzione generale è:. Qui una delle variabili di base è uguale a un numero costante:. Non c'è niente di esotico in questo, succede. Ovviamente, in questo caso, qualsiasi soluzione particolare conterrà una A in prima posizione.
Raramente, ma ci sono sistemi in cui il numero di equazioni è maggiore del numero di variabili... Tuttavia, il metodo Gauss funziona nelle condizioni più difficili. È necessario ridurre con calma la matrice espansa del sistema a una forma a gradini secondo l'algoritmo standard. Un tale sistema può essere incoerente, può avere infinite soluzioni e, stranamente, può avere un'unica soluzione.
Ripetiamo nel nostro consiglio: per sentirti a tuo agio quando risolvi un sistema usando il metodo gaussiano, dovresti riempirti la mano e risolvere almeno una dozzina di sistemi.
Soluzioni e risposte:
Esempio 2:
Soluzione:Scriviamo la matrice estesa del sistema e, usando trasformazioni elementari, portiamola in una forma graduale.
Trasformazioni elementari eseguite:
(1) La prima e la terza riga sono invertite.
(2) La prima riga moltiplicata per (-6) è stata aggiunta alla seconda riga. La prima riga moltiplicata per (-7) è stata aggiunta alla terza riga.
(3) La seconda riga moltiplicata per (–1) è stata aggiunta alla terza riga.
Come risultato di trasformazioni elementari, una stringa della forma, dove λ ≠ 0 .Ciò significa che il sistema è incompatibile.Risposta: nessuna soluzione.
Esempio 4:
Soluzione:Scriviamo la matrice estesa del sistema e, usando trasformazioni elementari, portiamola in una forma graduale:
Conversioni eseguite:
(1). Alla seconda riga è stata aggiunta la prima riga moltiplicata per 2. Alla terza riga è stata aggiunta la prima riga moltiplicata per 3.
Non c'è nessuno per il secondo passo , e la trasformazione (2) è finalizzata ad ottenerlo.
(2). La terza riga è stata aggiunta alla seconda moltiplicata per -3.
(3). La seconda e la terza riga sono state scambiate (riorganizzato il -1 risultante al secondo passaggio)
(4). La terza riga è stata aggiunta alla seconda moltiplicata per 3.
(5). Il segno delle prime due linee è stato cambiato (moltiplicato per –1), la terza linea è stata divisa per 14.
Inversione:
(1). Qui - variabili di base (che sono sui gradini), e - variabili libere (che non hanno ottenuto un passaggio).
(2). Esprimiamo le variabili di base in termini di variabili libere:
Dalla terza equazione: .
(3). Considera la seconda equazione:, soluzioni particolari:
Risposta: Decisione comune: 
Numeri complessi
In questa sezione, faremo conoscenza con il concetto numero complesso, tener conto di algebrico, trigonometrico e forma esemplare numero complesso. Impareremo anche come eseguire azioni con numeri complessi: addizione, sottrazione, moltiplicazione, divisione, elevamento a potenza ed estrazione della radice.
Per padroneggiare i numeri complessi, non è necessaria alcuna conoscenza speciale del corso di matematica superiore e il materiale è disponibile anche per uno studente. È sufficiente essere in grado di eseguire operazioni algebriche con numeri "ordinari" e ricordare la trigonometria.
Innanzitutto, ricordiamo i Numeri "ordinari". In matematica si chiamano insieme di numeri reali e indicato con la lettera R, o R (addensato). Tutti i numeri reali siedono sulla familiare linea dei numeri:
La compagnia dei numeri reali è molto variegata: qui ci sono interi, frazioni e numeri irrazionali. In questo caso, ogni punto dell'asse numerico corrisponde necessariamente a un certo numero reale.
Trovare soluzioni a un sistema lineareApplicazioni Windows portatili su Bodrenko.com
§2. Trovare soluzioni a un sistema lineare
Il teorema di Kronecker-Capelli stabilisce una condizione necessaria e sufficiente per la compatibilità di un sistema lineare, ma non fornisce un modo per trovare soluzioni a questo sistema.
In questa sezione cercheremo soluzioni al sistema lineare (3.1). Innanzitutto, consideriamo il caso più semplice di un sistema quadratico di equazioni lineari con un determinante diverso da zero della matrice di base, quindi procediamo a trovare l'insieme di tutte le soluzioni di un sistema lineare generale della forma (3.1).
1. Un sistema quadratico di equazioni lineari con determinante diverso da zero della matrice di base. Sia dato un sistema quadratico di equazioni lineari
con determinante diverso da zero della matrice principale
Dimostriamo che un tale sistema ha, e inoltre, una soluzione unica, e troveremo questa soluzione. In primo luogo, dimostriamo che il sistema (3.10) può avere una sola soluzione (cioè, dimostriamo l'unicità di una soluzione al sistema (3.10) sotto l'assunzione della sua esistenza).
Supponiamo che ci siano alcuni n numeri x 1, x 2, ..., xn tali che quando questi numeri sono sostituiti nel sistema (3.10), tutte le equazioni di questo sistema si trasformano in identità (cioè, c'è una soluzione al sistema ( 3.10) x 1, x 2, ..., x n). Quindi, moltiplicando le identità (3.10), rispettivamente, per i complementi algebrici A 1j, A 2j, ..., A nj elementi della colonna j-ro del determinante Δ della matrice (3.11) e quindi sommando le identità risultanti, si ottiene ottenere (per qualsiasi numero j, uguale a 1, 2, ..., n)
Tenendo conto che la somma dei prodotti degli elementi della i-esima colonna per i corrispondenti complementi algebrici degli elementi della colonna j-ro è uguale a zero per i ≠ j ed è uguale al determinante Δ della matrice (3.11 ) per i = j (vedi proprietà 4° dal comma 4 del § 2 del Cap. 1), si ricava dall'ultima uguaglianza
x j Δ = b 1 A 1j + b 2 A 2j + ... + b n A nj. (3.12)
Indichiamo con il simboloΔ
J (B io ) (o, più brevemente, il simboloΔ
J ) determinante ottenuto dal determinanteΔ
della matrice principale (3.11) sostituendo la sua j-esima colonna con una colonna di termini liberi b 1
, B 2
, ..., B n (mantenendo invariate tutte le altre colonne
Δ
).
Si noti che il membro di destra della (3.12) contiene esattamente il determinante Δ j (bi) (per convincersene basta scrivere lo sviluppo del determinante Δ j (bi) nei termini degli elementi della i-esima colonna ), e questa uguaglianza assume la forma
x j = Δ j (3.13)
Poiché il determinante della matrice (3.11) è diverso da zero, le uguaglianze (3.13) sono equivalenti alle relazioni
Quindi, abbiamo dimostrato che se soluzione x 1
, X 2
,...,NS n sistema (3.10) con determinanteΔ
della matrice principale (3.11) diversa da zero esiste, allora questa soluzione è determinata in modo univoco dalle formule (3.14).
Le formule (3.14) sono chiamate Le formule di Cramer.
Sottolineiamo ancora una volta che abbiamo finora ottenuto le formule di Cramer sotto l'assunzione dell'esistenza di una soluzione e ne dimostriamo l'unicità.
Resta da dimostrare l'esistenza di una soluzione al sistema (3.10). Per questo, in virtù del teorema di Kronecker-Capelli, è sufficiente dimostrare che il rango della matrice principale (3.11) è uguale al rango della matrice estesa (c'è anche un altro modo per dimostrare l'esistenza di una soluzione al sistema (3.10), che consiste nel verificare che i numeri x 1, x 2,..., х n, definiti dalle formule di Cramer (3.14), convertano in identità tutte le equazioni del sistema (3.10)
ma questo è ovvio, perché in virtù della relazione Δ ≠ 0, il rango della matrice principale è uguale a n, e il rango della matrice estesa (3.15) contenente n righe non può essere maggiore di n e quindi è uguale al rango della matrice principale.
Questo dimostra completamente che il sistema quadratico di equazioni lineari (3.10) con determinante diverso da zero della matrice di base ha, e inoltre, un'unica soluzione determinata dalle formule di Cramer (3.14).
L'asserzione che abbiamo dimostrato può essere stabilita ancora più facilmente in modo matriciale. Per fare ciò, sostituiamo (come nella sottosezione 1 del § 1) sistema (3.10) con l'equazione matriciale equivalente
AX = B, (3,16)
dove A è la matrice principale del sistema (3.11) e X e B sono colonne,
il primo dei quali è da determinare, e il secondo è dato.
Poiché il determinante della matrice A è diverso da zero, allora esiste una matrice inversa A -1 (vedi Sezione 7, Sezione 2, Capitolo 1).
Supponiamo che ci sia una soluzione al sistema (3.10), ad es. c'è una colonna X che rende l'equazione matriciale (3.16) un'identità. Moltiplicando l'identità indicata a sinistra per la matrice inversa -1 avremo
LA -1 (AX) = LA -1 B. (3,17)
Consideriamo ora che in virtù della proprietà combinatoria del prodotto di tre matrici (vedi sottosezione 2 del § 1 del Cap. 1) e in virtù della relazione A -1 A = E, dove E è la matrice identità (vedi § 7 del § 2 del Cap. 1), A -1 (AX) = (A -1 A) X = EX = X, quindi si ottiene da (3.17)
X = A -1 B. (3.18)
Espandendo l'uguaglianza (3.18) e tenendo conto della forma della matrice inversa (vedi formula A.41) dalla Sezione 7, Sezione 2, Cap. 1), otteniamo le formule di Cramer per gli elementi della colonna X.
Quindi, abbiamo dimostrato che se esiste una soluzione dell'equazione matriciale (3.16), allora è determinata in modo univoco dalla relazione (3.18), che è equivalente alle formule di Cramer.
È facile verificare che la colonna X definita dalla relazione (3.18) è in effetti una soluzione dell'equazione matriciale (3.16),
cioè, quando viene sostituito in questa equazione, la trasforma in un'identità. Infatti, se la colonna X è definita dall'uguaglianza (3.18), allora AX = A (A -1 B) = (AA -1) B = EB = B.
Quindi, se il determinante della matrice A è diverso da zero (cioè se questa matrice non è degenere), allora esiste, e inoltre, un'unica soluzione dell'equazione della matrice (3.16), definita dalla relazione (3.18), equivalente alle formule di Cramer.
Esempio. Troviamo la soluzione del sistema quadratico di equazioni lineari
con determinante diverso da zero della matrice principale
Nella misura in cui
quindi, in virtù delle formule di Cramer, l'unica soluzione del sistema in esame ha la forma x 1 = 1, x 2 = 2, x 3 = 3, x 4 = 4.
Il significato principale delle formule di Cramer è che danno un'espressione esplicita per risolvere un sistema quadratico di equazioni lineari (con un determinante diverso da zero) in termini di coefficienti delle equazioni e termini liberi. L'uso pratico delle formule di Cramer è associato a calcoli piuttosto macchinosi (per risolvere un sistema di n equazioni con n incognite, è necessario calcolare il determinante (n + 1) dell'ennesimo ordine). A ciò va aggiunto che se i coefficienti delle equazioni e dei termini liberi sono solo valori approssimativi di qualsiasi quantità fisica misurata o vengono arrotondati nel processo di calcolo, l'uso delle formule di Cramer può portare a grandi errori e in alcuni casi è inappropriato.
Nella Sezione 4, Capitolo 4, il metodo di regolarizzazione dovuto ad A.N. Tikhonov e ti permette di trovare una soluzione a un sistema lineare con un'accuratezza corrispondente all'accuratezza di specificare la matrice dei coefficienti delle equazioni e una colonna di termini liberi, e nel cap. 6 dà un'idea dei cosiddetti metodi iterativi per la risoluzione di sistemi lineari, che consentono di risolvere questi sistemi utilizzando approssimazioni successive di incognite.
In conclusione, notiamo che in questa sottosezione abbiamo escluso dalla considerazione il caso di nullità del determinante della matrice principale del sistema (3.10). Questo caso sarà contenuto nella teoria generale dei sistemi di m equazioni lineari con n incognite, presentata nella prossima sottosezione.
2. Trovare tutte le soluzioni di un sistema lineare generale. Consideriamo ora un sistema generale di m equazioni lineari con n incognite (3.1). Supponiamo che questo sistema sia consistente e che il rango delle sue matrici principali ed estese sia uguale a r. Senza perdita di generalità, possiamo assumere che il minore fondamentale della matrice principale (3.2) sia nell'angolo in alto a sinistra di questa matrice (il caso generale si riduce a questo caso permutando equazioni e incognite nel sistema (3.1)).
Allora le prime r righe sia della matrice principale (3.2) che della matrice estesa (3.8) sono le righe base di queste matrici (poiché i ranghi delle matrici principale ed estesa sono entrambi uguali a r, il minore fondamentale della matrice principale sarà contemporaneamente il minore di base della matrice estesa) , e, per il Teorema 1.6 sul minore di base, ciascuna delle righe della matrice estesa (1.8), a partire dalla (r + 1) esima riga, è una combinazione lineare di le prime r righe di questa matrice.
In termini di sistema (3.1), ciò significa che ciascuna delle equazioni di questo sistema, a partire dalla (r + 1) esima equazione, è una combinazione lineare (cioè una conseguenza) delle prime r equazioni di questo sistema ( cioè, qualsiasi soluzione delle prime r equazioni del sistema (3.1) si trasforma in identità e tutte le successive equazioni di questo sistema).
Quindi, è sufficiente trovare tutte le soluzioni delle sole prime r equazioni del sistema (3.1). Consideriamo le prime r equazioni del sistema (3.1), scrivendole nella forma
Se diamo alle incognite xr + 1, ..., xn valori completamente arbitrari cr + 1, ..., cn, allora il sistema (1.19) si trasformerà in un sistema quadratico di r equazioni lineari per r incognite x 1, x 2, ..., х r, e il determinante della matrice di base di questo sistema è un minore di base diverso da zero della matrice (3.2). In virtù dei risultati della sezione precedente, questo sistema (3.19) ha un'unica soluzione definita dalle formule di Cramer, cioè, per cr + 1, ..., cn scelti arbitrariamente, esiste un'unica collezione r di numeri c 1, ..., cr, convertendo tutte le equazioni del sistema (3.19) in identità e definite dalle formule di Cramer.
Per scrivere questa unica soluzione, concordiamo di indicare con il simbolo M j (di) il determinante ottenuto dal minore fondamentale M della matrice (3.2) sostituendo la sua colonna j-ro con una colonna di numeri d 1, d 2, ..., di, ..., dr (mantenendo invariate tutte le altre colonne M). Quindi, scrivendo la soluzione del sistema (3.19) utilizzando le formule di Cramer e sfruttando la proprietà lineare del determinante, si ottiene
Le formule (3.20) esprimono i valori delle incognite xj = cj (j = 1, 2, ......, r) in termini di coefficienti delle incognite, termini liberi e parametri arbitrari con r + 1, ...., con n.
Dimostriamolo le formule (3.20) contengono qualsiasi soluzione del sistema (3.1)... Siano infatti c (0) 1, c (0) 2, ..., c (0) r, c (0) r + 1, ..., c (0) n una soluzione arbitraria del sistema indicato . Allora è anche una soluzione al sistema (3.19). Ma dal sistema (3.19) le quantità c (0) 1, c (0) 2, ..., c (0) r, sono determinate in termini delle quantità c (0) r + 1, ..., c (0) n univocamente e precisamente dalle formule di Cramer (3.20). Quindi, per c r + 1 = c (0)
r + 1, ..., insieme a n = c (0)
n
le formule (3.20) ci danno solo la soluzione considerata c (0)
1
, C (0)
2
, ..., C (0)
R , C (0)
r + 1, ..., C (0)
n .
Commento. Se il rango r delle matrici principali ed estese del sistema (3.1) è uguale al numero di incognite n, allora in questo caso le relazioni (3.20) passano alle formule
determinare l'unica soluzione del sistema (3.1). Quindi, il sistema (3.1) ha un'unica soluzione (cioè è definito) a condizione che il rango r delle sue matrici principali ed estese sia uguale al numero di incognite n (e sia minore o uguale al numero di equazioni m).
Esempio. Trova tutte le soluzioni al sistema lineare
È facile verificare che il rango di entrambe le matrici principali ed estese di questo sistema è uguale a due (cioè questo sistema è coerente), e possiamo assumere che il minore di base M sia nell'angolo in alto a sinistra della matrice principale , cioè 
... Ma poi, scartando le ultime due equazioni e ponendo arbitrariamente con 3 e con 4, otteniamo il sistema
x 1 - x 2 = 4 - c 3 + c 4,
x 1 + x 2 = 8 - 2c 3 - 3c 4,
da cui, in virtù delle formule di Cramer, si ottengono i valori
x 1 = do 1 = 6 - 3/2 do 3 - do 4, x 2 = do 2 = 2 - 1/2 do 3 - 2 c 4. (3.22)
Quindi, i quattro numeri
(6 - 3/2 do 3 - do 4, 2 - 1/2 do 3 - 2c 4, do 3, do 4) (3.23)
a caso impostare i valori c 3 e c 4 formano una soluzione del sistema (3.21) e la riga (3.23) contiene tutte le soluzioni di questo sistema.
3. Proprietà dell'insieme delle soluzioni di un sistema omogeneo. Consideriamo ora un sistema omogeneo di m equazioni lineari con n incognite (3.7), assumendo, come sopra, che la matrice (3.2) abbia rango uguale a r, e che il minore fondamentale si trovi nell'angolo superiore sinistro di tale matrice. Poiché questa volta tutti i b i sono uguali a zero, invece delle formule (3.20) otteniamo le seguenti formule:
esprimendo i valori delle incognite x j = c j (j = 1, 2, ..., r) in termini di coefficienti delle incognite e valori arbitrariamente dati c r + 1, ..., c n. In virtù di quanto dimostrato nel paragrafo precedente le formule (3.24) contengono qualsiasi soluzione al sistema omogeneo (3.7).
Verifichiamo ora che la collezione di tutte le soluzioni del sistema omogeneo (3.7) forma lo spazio lineare.
Sia X 1 = (x (1) 1, x (1) 2, ..., x (1) n) e X 2 = (x (2) 1, x (2) 2, ..., x ( 2) n) sono due soluzioni arbitrarie del sistema omogeneo (3.7), e è un qualsiasi numero reale. Poiché ogni soluzione del sistema omogeneo (3.7) è un elemento dello spazio lineare А n di tutti gli insiemi ordinati di n numeri, basta provare che ciascuno dei due insiemi
X 1 + X 2 = (x (1) 1 + x (2) 1, ..., x (1) n + x (2) n)
X 1 = (λ x (1) 1, ..., λ x (1) n)
è anche una soluzione del sistema omogeneo (3.7).
Consideriamo una qualsiasi equazione del sistema (3.7), per esempio i-esima equazione, e sostituire in questa equazione al posto degli elementi incogniti degli insiemi specificati. Tenendo conto che X 1 e X 2 sono soluzioni di un sistema omogeneo, avremo
e questo significa che le collezioni X 1 + X 2 e λ X 1 sono soluzioni del sistema omogeneo (3.7).
Quindi, l'insieme di tutte le soluzioni del sistema omogeneo (3.7) forma uno spazio lineare, che indichiamo con R.
Troviamo la dimensione di questo spazio R e costruiamo in esso una base.
Dimostriamo che sotto l'ipotesi che il rango della matrice del sistema omogeneo (3.7) sia uguale a r, lo spazio lineare R di tutte le soluzioni del sistema omogeneo (3.7) è isomorfo allo spazio lineare A n-r di tutte le raccolte ordinate (n -r) di numeri(l'n spazio A m è stato introdotto nell'Esempio 3, Sezione 1, Sezione 1, Capitolo 2).
Associamo ogni soluzione (c 1, ..., c r, c r + 1, ..., c n) del sistema omogeneo (3.7) ad un elemento (c r + 1, ..., c n) dello spazio UN n-r Poiché i numeri c r + 1, ..., c n possono essere scelti arbitrariamente e per ogni scelta utilizzando le formule (3.24) determinano in modo univoco la soluzione del sistema (3.7), la corrispondenza che abbiamo stabilito è uno a uno... Si noti inoltre che se gli elementi c (1) r + 1, ..., c (1) n e c (2) r + 1, ..., c (2) n dello spazio UN n-r corrispondono agli elementi (c (1) 1, ..., c (1) r, c (1) r + 1, ..., c (1) n) e (c (2) 1, ... , c (2) r, c (2) r + 1, ..., c (2) n) dello spazio R, quindi le formule (3.24) implicano immediatamente che l'elemento (c (1) r + 1 + c (2 ) r + 1, ..., c (1) n + c (2) n) corrisponde all'elemento (c (1) 1 + c (2) 1, ..., c (1) r + c (2) r, c (1) r + 1 + c (2) r + 1, ..., c (1) n + c (2) n), e l'elemento (λ c (1) r + 1, ... , c (1) n) ad ogni reale corrisponde un elemento (λ c (1) 1, ..., c (1) r, λ c (1) r + 1, . .., c (1 ) n). Questo prova che la corrispondenza che abbiamo stabilito è un isomorfismo.
Quindi, lo spazio lineare R di tutte le soluzioni del sistema omogeneo (3.7) con n incognite e rango della matrice principale uguale a r è isomorfo allo spazio UN n-r e, quindi, ha dimensione n - r.
Qualsiasi insieme di (n - r) soluzioni linearmente indipendenti del sistema omogeneo (3.7) forma (in virtù del Teorema 2.5) una base nello spazio R di tutte le soluzioni e si chiama insieme fondamentale di soluzioni del sistema omogeneo (3.7) .
Per costruire un insieme fondamentale di soluzioni, puoi andare da qualsiasi base di spazio UN n-r... L'insieme delle soluzioni del sistema (3.7) corrispondente a questa base, per isomorfismo, sarà linearmente indipendente e quindi sarà un insieme fondamentale di soluzioni.
Si distingue in particolare l'insieme fondamentale delle soluzioni del sistema (3.7), che corrisponde alla base più semplice e 1 = (1, 0, 0, ..., 0), e 2 = (1, 1, 0, ... , 0), ... , е nr = (0, 0, 0, ..., 1) dello spazio UN n-r e chiamò l'insieme fondamentale normale delle soluzioni del sistema omogeneo (3.7).
Sotto le ipotesi di cui sopra circa il rango e la posizione del minore di base, in virtù delle formule (3.24), l'insieme fondamentale normale di soluzioni al sistema omogeneo (3.7) ha la forma:
Per definizione della base, qualsiasi soluzione X del sistema omogeneo (3.7) può essere rappresentata nella forma
X = C 1 X 1 + C 2 X 2 + ... + C n-r X n-r, (3.26)
dove C 1, C 2, ..., C n-r sono alcune costanti. Poiché la formula (3.26) contiene qualsiasi soluzione del sistema omogeneo (3.7), questa formula fornisce una soluzione generale del sistema omogeneo considerato.
Esempio. Consideriamo un sistema omogeneo di equazioni:
corrispondente al sistema disomogeneo (3.21) analizzato nell'esempio alla fine della sezione precedente. Lì abbiamo scoperto che il rango r della matrice di questo sistema è uguale a due e abbiamo preso come base il minore nell'angolo in alto a sinistra della matrice indicata.
Ripetendo il ragionamento alla fine del paragrafo precedente, invece delle formule (3.22), si ottengono le relazioni
do 1 = - 3/2 do 3 - do 4, do 2 = - 1/2 do 3 - 2 do 4,
valido per c 3 e c 4 scelti arbitrariamente. Usando queste relazioni (assumendo prima c 3 = 1, c 4 = 0, e poi c 3 = 0, c 4 = 1) si ottiene un normale insieme fondamentale di due soluzioni del sistema (3.27):
X 1 = (-3 / 2, -1 / 2,1,0), X 2 = (-1, -2, 0,1). (3.28)
dove C 1 e C 2 sono costanti arbitrarie.
Per concludere questa sottosezione, stabiliamo una connessione tra le soluzioni del sistema lineare disomogeneo (3.1) e il corrispondente sistema omogeneo (3.7) (con gli stessi coefficienti per le incognite). Dimostriamo le seguenti due affermazioni.
1°. La somma di qualsiasi soluzione del sistema disomogeneo (3.1) con qualsiasi soluzione del corrispondente sistema omogeneo (3.7) è una soluzione del sistema (3.1).
Infatti, se c 1, ..., cn è una soluzione del sistema (3.1), ad 1, ..., dn è una soluzione del corrispondente sistema omogeneo (3.7), allora, sostituendo in qualsiasi (per esempio, in l'ith ) l'equazione del sistema (3.1) al posto delle incognite c 1 + d 1, ..., cn + dn, si ottiene
Q.E.D.
2°. La differenza di due soluzioni arbitrarie del sistema disomogeneo (3.1) è una soluzione del corrispondente sistema omogeneo (3.7).
Infatti, se c "1, ..., c" n e c "1, ..., c" n sono due soluzioni arbitrarie del sistema (3.1), allora, sostituendo in una qualsiasi (per esempio, nell'i-esima) equazione del sistema (3.7) al posto delle incognite c "1 - c" 1, ..., c "n - c" n si ottiene
Q.E.D.
Dalle affermazioni provate segue che, trovando una soluzione del sistema disomogeneo (3.1) e sommandola a ciascuna soluzione del corrispondente sistema omogeneo (3.7), si ottengono tutte le soluzioni del sistema disomogeneo (3.1).
In altre parole, la somma di una soluzione particolare del sistema disomogeneo (3.1) e la soluzione generale del corrispondente sistema omogeneo (3.7) dà la soluzione generale del sistema disomogeneo (3.1).
Come soluzione particolare del sistema disomogeneo (3.1), è naturale assumerne la soluzione (in questo caso si assume, come sopra, che i ranghi delle matrici principali ed estese del sistema (3.1) siano uguali a r e che il minore di base è nell'angolo in alto a sinistra di queste matrici)
che si otterrà se tutti i numeri c r + 1, ..., c n sono posti uguali a zero nelle formule (3.20). Sommando questa soluzione particolare con la soluzione generale (3.26) del corrispondente sistema omogeneo, si ottiene la seguente espressione per la soluzione generale del sistema disomogeneo (3.1):
X = X 0 + C 1 X 1 + C 2 X 2 + ... + C n-r X n-r. (3.30)
In questa espressione, X 0 denota una particolare soluzione (3.29), C 1, C 2, ..., C nr sono costanti arbitrarie e X 1, X 2, ..., X nr sono elementi dell'insieme fondamentale normale di soluzioni (3.25) corrispondente sistema omogeneo.
Quindi, per il sistema disomogeneo (3.21) considerato alla fine del paragrafo precedente, la soluzione particolare della forma (3.29) è uguale a X 0 = (6,2,0,0).
Sommando questa soluzione particolare con la soluzione generale (3.28) del corrispondente sistema omogeneo (3.27), si ottiene la seguente soluzione generale del sistema disomogeneo (3.21):
X = (6,2,0,0) + C 1 (-3 / 2, -1 / 2,1,0) + C 2 (-1, -2, 0,1). (3.31)
Qui C 1 e C 2 sono costanti arbitrarie.
4. Considerazioni conclusive sulla risoluzione di sistemi lineari. Metodi per la risoluzione di sistemi lineari sviluppati nei paragrafi precedenti
si scontra con la necessità di calcolare il rango della matrice e trovarne il minore di base. Trovato il minore di base, la soluzione si riduce alla tecnica del calcolo dei determinanti e all'uso delle formule di Cramer.
Per calcolare il rango di una matrice, puoi utilizzare la seguente regola: nel calcolo del rango di una matrice si dovrebbe passare dai minori degli ordini inferiori ai minori degli ordini superiori; inoltre, se è già stato trovato un minore di ordine k diverso da zero, allora solo i minori di ordine (k + 1) confinanti(cioè contenente un M minore) questo minore è M; se tutti i minori di ordine confinanti (k + 1) sono uguali a zero, il rango della matrice è uguale a k(infatti, nel caso indicato, tutte le righe (colonne) della matrice appartengono all'inviluppo lineare delle sue k righe (colonne), all'intersezione delle quali vi è una M minore, e la dimensione dell'inviluppo lineare indicato è uguale a k).
Indichiamo un'altra regola per calcolare il rango di una matrice. Si noti che con righe (colonne) di una matrice si può produrre tre operazioni elementari che non modificano il rango di questa matrice: 1) permutazione di due righe (o due colonne), 2) moltiplicazione di una riga (o colonna) per un qualsiasi fattore diverso da zero, 3) aggiunta a una riga (colonna) di una combinazione lineare arbitraria di altre righe (colonne) (queste tre operazioni non modificano il rango della matrice per il fatto che le operazioni 1) e 2) non modificano il numero massimo di righe (colonne) linearmente indipendenti della matrice, e l'operazione 3) ha la proprietà che l'inviluppo lineare di tutte le righe (colonne) disponibili prima di questa operazione, coincide con l'inviluppo lineare di tutte le righe (colonne) ottenuto dopo questa operazione).
Diciamo che la matrice || a ij ||, contenente m righe e n colonne, ha diagonale forma, se tutti i suoi elementi sono uguali a zero, diversi da a 11, a 22, .., a rr, dove r = min (m, n). Il rango di tale matrice è ovviamente r.
Assicuriamoci che mediante tre operazioni elementari qualsiasi matrice
può essere ridotto alla forma diagonale(che ci permette di calcolarne il rango).
Infatti, se tutti gli elementi della matrice (3.31) sono uguali a zero, allora questa matrice è già stata ridotta alla forma diagonale. Se il mat-
Se il grafo (3.31) ha elementi diversi da zero, allora permutando due righe e due colonne è possibile ottenere che l'elemento a 11 sia diverso da zero. Dopodiché, moltiplicando la prima riga della matrice per 11 -1, trasformeremo l'elemento a 11 in uno. Sottraendo ulteriormente dalla colonna j-ro della matrice (per j = 2, 3, ..., n) la prima colonna, moltiplicata per a i1, e quindi sottraendo dalla i-esima riga (per i = 2, 3 , ..., n) la prima riga, moltiplicata per i1, otteniamo invece della (3.31) una matrice della forma seguente:
Eseguendo le operazioni da noi già descritte con la matrice, presa nel frame, e continuando ad agire in modo analogo, dopo un numero finito di passi otterremo una matrice di forma diagonale.
I metodi per risolvere i sistemi lineari descritti nei paragrafi precedenti, che alla fine utilizzano l'apparato delle formule di Cramer, possono portare a grandi errori nel caso in cui i valori dei coefficienti delle equazioni e dei termini liberi siano dati approssimativamente o quando questi valori sono arrotondati nel processo di calcolo.
Innanzitutto, ciò si riferisce al caso in cui la matrice corrispondente al determinante principale (o minore fondamentale) è mal condizionato(cioè, quando variazioni "piccole" negli elementi di questa matrice corrispondono a variazioni "grandi" negli elementi della matrice inversa). Naturalmente, in questo caso, la soluzione del sistema lineare sarà instabile(cioè, i cambiamenti "grandi" nella soluzione corrisponderanno a cambiamenti "piccoli" nei valori dei coefficienti delle equazioni e dei termini liberi).
Queste circostanze portano alla necessità di sviluppare sia altri algoritmi teorici (diversi dalle formule di Cramer) per trovare una soluzione sia metodi numerici per risolvere sistemi lineari.
Nella Sezione 4, Capitolo 4, faremo conoscenza con con il metodo della regolarizzazione A.N. Tikhonov trovare il cosiddetto normale(cioè la soluzione più vicina all'origine) del sistema lineare.
Il capitolo 6 fornirà informazioni di base sul cosiddetto metodi iterativi soluzioni di sistemi lineari che consentono di risolvere questi sistemi utilizzando approssimazioni successive di incognite.
Un sistema di m equazioni lineari con n incognite chiamato un sistema della forma
dove un ij e b io (io=1,…,m; B=1,…,n) Sono alcuni numeri noti, e x 1, ..., x n- sconosciuto. Nella designazione dei coefficienti un ij primo indice io denota il numero di equazione, e il secondo J- il numero dell'incognita in cui si trova questo coefficiente.
Scriveremo i coefficienti per le incognite sotto forma di matrice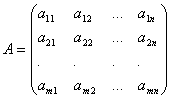 
, che chiameremo matrice di sistema.
I numeri a destra delle equazioni b 1, ..., b m sono chiamati membri liberi.
L'aggregato n numeri c 1, ..., c n chiamato decisione del sistema dato, se ogni equazione del sistema diventa uguaglianza dopo la sostituzione di numeri in essa c 1, ..., c n invece delle corrispondenti incognite x 1, ..., x n.
Il nostro compito sarà quello di trovare soluzioni al sistema. In questo caso si possono verificare tre situazioni:
Un sistema di equazioni lineari che ha almeno una soluzione si chiama giunto... Altrimenti, ad es. se il sistema non ha soluzioni, allora si chiama incoerente.
Considera i modi per trovare soluzioni al sistema.
METODO A MATRICE PER LA SOLUZIONE DI SISTEMI DI EQUAZIONI LINEARI
Le matrici consentono di scrivere in modo conciso un sistema di equazioni lineari. Sia dato un sistema di 3 equazioni con tre incognite:
Considera la matrice del sistema 
e colonne di matrice di termini sconosciuti e liberi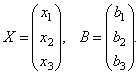 
Troviamo un lavoro
quelli. come risultato del prodotto, otteniamo i membri di sinistra delle equazioni di questo sistema. Quindi, usando la definizione di uguaglianza delle matrici, questo sistema può essere scritto nella forma
o più breve UN∙X = B.
qui matrici UN e B sono noti, e la matrice X sconosciuto. Anche lei deve essere trovata, tk. i suoi elementi sono la soluzione a questo sistema. Questa equazione è chiamata equazione della matrice.
Sia il determinante della matrice diverso da zero | UN| 0. Quindi l'equazione della matrice viene risolta come segue. Moltiplichiamo entrambi i membri dell'equazione a sinistra per la matrice A -1, l'inverso della matrice UN:. Nella misura in cui LA -1 LA = MI e E∙X = X, quindi otteniamo la soluzione dell'equazione matriciale nella forma X = LA -1 SI .
Si noti che poiché la matrice inversa può essere trovata solo per matrici quadrate, il metodo delle matrici può risolvere solo quei sistemi in cui il numero di equazioni coincide con il numero di incognite... Tuttavia, la rappresentazione matriciale del sistema è possibile anche nel caso in cui il numero di equazioni non sia uguale al numero di incognite, allora la matrice UN non sarà quadrato e quindi è impossibile trovare una soluzione al sistema nella forma X = LA -1 SI.
Esempi. Risolvere sistemi di equazioni.
REGOLA DI CRAMERA
Consideriamo un sistema di 3 equazioni lineari con tre incognite:
Determinante del terzo ordine corrispondente alla matrice del sistema, cioè composto da coefficienti con incognite,
chiamato determinante del sistema.
Componiamo altri tre determinanti come segue: sostituiamo nel determinante D successivamente le colonne 1, 2 e 3 con una colonna di membri liberi
Allora si può dimostrare il seguente risultato.
Teorema (regola di Cramer). Se il determinante del sistema è Δ ≠ 0, allora il sistema in esame ha una e una sola soluzione, e
Prova... Quindi, consideriamo un sistema di 3 equazioni con tre incognite. Moltiplichiamo la prima equazione del sistema per il complemento algebrico un 11 elemento un 11, 2a equazione - su un 21 e 3 - su un 31:
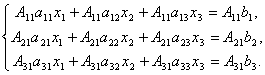
Aggiungiamo queste equazioni:
Diamo un'occhiata a ciascuna delle parentesi e al lato destro di questa equazione. Per il teorema sullo sviluppo del determinante rispetto agli elementi della prima colonna
Allo stesso modo, si può dimostrare che e.
Infine, è facile vedere che 
Quindi, otteniamo l'uguaglianza:.
Quindi, .
Le uguaglianze e si ricavano in modo simile, donde segue l'asserzione del teorema.
Quindi, notiamo che se il determinante del sistema è Δ ≠ 0, allora il sistema ha un'unica soluzione e viceversa. Se il determinante del sistema è uguale a zero, allora il sistema ha un insieme infinito di soluzioni o non ha soluzioni, ad es. incoerente.
Esempi. Risolvi il sistema di equazioni
METODO GAUSS
I metodi precedentemente considerati possono essere utilizzati per risolvere solo quei sistemi in cui il numero di equazioni coincide con il numero di incognite e il determinante del sistema deve essere diverso da zero. Il metodo di Gauss è più universale ed è adatto a sistemi con qualsiasi numero di equazioni. Consiste nella successiva eliminazione delle incognite dalle equazioni del sistema.
Consideriamo ancora un sistema di tre equazioni con tre incognite:
.
Lasciamo invariata la prima equazione, e dalla seconda e dalla terza escludiamo i termini contenenti x 1... Per questo, dividiamo la seconda equazione per un 21 e moltiplicare per - un 11 e poi aggiungilo alla prima equazione. Allo stesso modo, dividiamo la terza equazione per un 31 e moltiplicare per - un 11, quindi aggiungere al primo. Di conseguenza, il sistema originale assumerà la forma:
Ora escludiamo dall'ultima equazione il termine contenente x 2... Per fare ciò, dividi la terza equazione per, moltiplica per e aggiungi alla seconda. Avremo quindi un sistema di equazioni:
Quindi, dall'ultima equazione è facile trovare x 3, quindi dalla 2a equazione x 2 e infine dal 1 - x 1.
Quando si utilizza il metodo gaussiano, le equazioni possono essere scambiate secondo necessità.
Spesso, invece di scrivere un nuovo sistema di equazioni, si limitano a scrivere la matrice estesa del sistema:
e poi portarlo ad una forma triangolare o diagonale usando trasformazioni elementari.
A trasformazioni elementari matrici includono le seguenti trasformazioni:
- riordino di righe o colonne;
- moltiplicare una stringa per un numero diverso da zero;
- aggiungendo altre righe a una riga.
Esempi: Risolvere sistemi di equazioni utilizzando il metodo gaussiano.
Quindi, il sistema ha un numero infinito di soluzioni.
Indagare un sistema di equazioni agebraiche lineari (SLAE) per la compatibilità significa scoprire se questo sistema ha soluzioni o meno. Bene, se ci sono soluzioni, indica quante ce ne sono.
Abbiamo bisogno di informazioni dall'argomento "Sistema di equazioni algebriche lineari. Termini di base. Notazione matriciale". In particolare, abbiamo bisogno di concetti come la matrice del sistema e la matrice estesa del sistema, poiché è su di essi che si basa la formulazione del teorema di Kronecker-Capelli. Come al solito, la matrice del sistema sarà indicata con la lettera $ A $ e la matrice estesa del sistema con la lettera $ \ widetilde (A) $.
Teorema di Kronecker-Capelli
Il sistema di equazioni algebriche lineari è consistente se e solo se il rango della matrice del sistema è uguale al rango della matrice estesa del sistema, cioè $ \ squilla A = \ squilla \ widetilde (A) $.
Vi ricordo che un sistema si dice giunto se ha almeno una soluzione. Il teorema di Kronecker-Capelli afferma quanto segue: se $ \ rang A = \ rang \ widetilde (A) $, allora esiste una soluzione; se $ \ rang A \ neq \ rang \ widetilde (A) $, allora questo SLAE non ha soluzioni (incoerente). La risposta alla domanda sul numero di queste soluzioni è data da un corollario del teorema di Kronecker-Capelli. Nella formulazione del corollario viene utilizzata la lettera $ n $, che è uguale al numero di variabili del dato SLAE.
Corollario del teorema di Kronecker-Capelli
- Se $ \ rang A \ neq \ rang \ widetilde (A) $, allora lo SLAE è incoerente (non ha soluzioni).
- Se $ \ squilla A = \ squilla \ widetilde (A)< n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
- Se $ \ rang A = \ rang \ widetilde (A) = n $, allora lo SLAE è definito (ha esattamente una soluzione).
Si noti che il teorema di cui sopra e il suo corollario non indicano come trovare la soluzione allo SLAE. Con il loro aiuto, si può solo scoprire se queste soluzioni esistono o meno, e se esistono, allora quante.
Esempio 1
Esplora SLAE $ \ left \ (\ begin (allineato) & -3x_1 + 9x_2-7x_3 = 17; \\ & -x_1 + 2x_2-4x_3 = 9; \\ & 4x_1-2x_2 + 19x_3 = -42. \ End (allineato ) \ destra $ per compatibilità Se SLAE è compatibile, indicare il numero di soluzioni.
Per scoprire l'esistenza di soluzioni di un dato SLAE, usiamo il teorema di Kronecker-Capelli. Abbiamo bisogno della matrice del sistema $ A $ e della matrice estesa del sistema $ \ widetilde (A) $, le scriviamo:
$$ A = \ left (\ begin (array) (ccc) -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \ end (array) \ right); \; \ widetilde (A) = \ sinistra (\ inizio (array) (ccc | c) -3 & 9 & -7 & 17 \\ -1 & 2 & -4 & 9 \\ 4 & -2 & 19 & -42 \ fine (array) \ destra). $$
Trova $ \ rang A $ e $ \ rang \ widetilde (A) $. Ci sono molti modi per farlo, alcuni dei quali sono elencati nella sezione Matrix Rank. Di solito, vengono utilizzati due metodi per studiare tali sistemi: "Calcolo del rango di una matrice per definizione" o "Calcolo del rango di una matrice con il metodo delle trasformazioni elementari".
Metodo numero 1. Calcolo dei ranghi per definizione.
Per definizione, il rango è l'ordine più alto dei minori di matrice, tra i quali vi è almeno uno diverso da zero. Solitamente lo studio inizia con i minori del primo ordine, ma qui è più conveniente iniziare subito a calcolare il minore del terzo ordine della matrice $ A $. Gli elementi del terzo ordine minore si trovano all'intersezione di tre righe e tre colonne della matrice in esame. Poiché la matrice $ A $ contiene solo 3 righe e 3 colonne, il minore di terzo ordine della matrice $ A $ è il determinante della matrice $ A $, ovvero $ \ Delta A $. Per calcolare il determinante, applichiamo la formula n. 2 dall'argomento "Formule per il calcolo dei determinanti del secondo e del terzo ordine":
$$ \ Delta A = \ sinistra | \ begin (array) (ccc) -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \ end (array) \ right | = -21. $$
Quindi, esiste un minore di terzo ordine della matrice $ A $, che non è uguale a zero. È impossibile comporre un minore del quarto ordine, poiché richiede 4 righe e 4 colonne e nella matrice $ A $ ci sono solo 3 righe e 3 colonne. Quindi, l'ordine più alto dei minori della matrice $ A $, tra i quali ce n'è almeno uno diverso da zero, è uguale a 3. Pertanto, $ \ rang A = 3 $.
Dobbiamo anche trovare $ \ rang \ widetilde (A) $. Diamo un'occhiata alla struttura della matrice $ \ widetilde (A) $. La matrice $ \ widetilde (A) $ contiene gli elementi della matrice $ A $ e abbiamo scoperto che $ \ Delta A \ neq 0 $. Pertanto, la matrice $ \ widetilde (A) $ ha un minore di terzo ordine diverso da zero. Non possiamo comporre i minori di quarto ordine della matrice $ \ widetilde (A) $, quindi concludiamo: $ \ rang \ widetilde (A) = 3 $.
Poiché $ \ rang A = \ rang \ widetilde (A) $, secondo il teorema di Kronecker-Capelli, il sistema è consistente, cioè ha una soluzione (almeno una). Per indicare il numero di soluzioni, teniamo conto che il nostro SLAE contiene 3 incognite: $ x_1 $, $ x_2 $ e $ x_3 $. Poiché il numero di incognite è $ n = 3 $, concludiamo: $ \ rang A = \ rang \ widetilde (A) = n $, quindi, secondo il corollario del teorema di Kronecker-Capelli, il sistema è definito, cioè ha una sola soluzione.
Il problema è stato risolto. Quali sono gli svantaggi e i vantaggi di questo metodo? Per prima cosa, parliamo dei pro. Per prima cosa, abbiamo solo bisogno di trovare un determinante. Successivamente, abbiamo immediatamente tratto una conclusione sul numero di soluzioni. Di solito, nei calcoli standard standard, vengono forniti sistemi di equazioni che contengono tre incognite e hanno un'unica soluzione. Per tali sistemi questo metodoè molto conveniente, perché sappiamo in anticipo che c'è una soluzione (altrimenti non ci sarebbe nessun esempio in un calcolo tipico). Quelli. dobbiamo solo mostrare la presenza di una soluzione dei più modo veloce... In secondo luogo, il valore calcolato del determinante della matrice del sistema (cioè $ \ Delta A $) tornerà utile dopo: quando inizieremo a risolvere il dato sistema con il metodo di Cramer o usando la matrice inversa.
Tuttavia, il metodo di calcolo del rango è per definizione indesiderabile se la matrice del sistema $ A $ è rettangolare. In questo caso, è meglio utilizzare il secondo metodo, che verrà discusso di seguito. Inoltre, se $ \ Delta A = 0 $, allora non possiamo dire nulla sul numero di soluzioni di un dato SLAE disomogeneo. Forse SLAE ha un numero infinito di soluzioni, o forse nessuna. Se $ \ Delta A = 0 $, sono necessarie ulteriori ricerche, che sono spesso ingombranti.
Riassumendo quanto detto, rilevo che il primo metodo va bene per quegli SLAE in cui la matrice del sistema è quadrata. In questo caso, lo stesso SLAE contiene tre o quattro incognite ed è tratto da calcoli tipici standard o da lavori di controllo.
Metodo numero 2. Calcolo del rango con il metodo delle trasformazioni elementari.
Questo metodo è descritto in dettaglio nell'argomento correlato. Inizieremo a calcolare il rango della matrice $ \ widetilde (A) $. Perché esattamente le matrici $ \ widetilde (A) $ e non $ A $? Il fatto è che la matrice $ A $ è una parte della matrice $ \ widetilde (A) $, quindi, calcolando il rango della matrice $ \ widetilde (A) $, troveremo contemporaneamente il rango della matrice $ A $.
\ begin (allineato) & \ widetilde (A) = \ left (\ begin (array) (ccc | c) -3 & 9 & -7 & 17 \\ -1 & 2 & -4 & 9 \\ 4 & - 2 & 19 & -42 \ end (array) \ right) \ rightarrow \ left | \ text (scambia prima e seconda riga) \ right | \ rightarrow \\ & \ rightarrow \ left (\ begin (array) (ccc | c) -1 & 2 & -4 & 9 \\ -3 & 9 & -7 & 17 \\ 4 & -2 & 19 & - 42 \ end (array) \ right) \ begin (array) (l) \ phantom (0) \\ r_2-3r_1 \\ r_3 + 4r_1 \ end (array) \ rightarrow \ left (\ begin (array) (ccc | c) -1 & 2 & -4 & 9 \\ 0 & 3 & 5 & -10 \\ 0 & 6 & 3 & -6 \ fine (matrice) \ destra) \ inizio (matrice) (l) \ fantasma ( 0 ) \\ \ fantasma (0) \\ r_3-2r_2 \ end (array) \ rightarrow \\ & \ rightarrow \ left (\ begin (array) (ccc | c) -1 & 2 & -4 & 9 \\ 0 & 3 & 5 & -10 \\ 0 & 0 & -7 & 14 \ fine (array) \ destra) \ fine (allineato)
Abbiamo trasformato la matrice $ \ widetilde (A) $ in una forma a gradini. La matrice a gradini risultante ha tre righe diverse da zero, quindi il suo rango è 3. Pertanto, il rango della matrice $ \ widetilde (A) $ è 3, ovvero $ \ squilla \ widetilde (A) = 3 $. Effettuando trasformazioni con gli elementi della matrice $ \ widetilde (A) $, abbiamo trasformato contemporaneamente gli elementi della matrice $ A $, posti fino alla linea. Anche la matrice $ A $ è a gradini: $ \ left (\ begin (array) (ccc) -1 & 2 & -4 \\ 0 & 3 & 5 \\ 0 & 0 & -7 \ end (array) \ right ) $. Conclusione: anche il rango della matrice $ A $ è 3, ad es. $ \ ha suonato A = 3 $.
Poiché $ \ rang A = \ rang \ widetilde (A) $, secondo il teorema di Kronecker-Capelli, il sistema è consistente, cioè ha una soluzione. Per indicare il numero di soluzioni, teniamo conto che il nostro SLAE contiene 3 incognite: $ x_1 $, $ x_2 $ e $ x_3 $. Poiché il numero di incognite è $ n = 3 $, concludiamo: $ \ rang A = \ rang \ widetilde (A) = n $, quindi, secondo il corollario del teorema di Kronecker-Capelli, il sistema è definito, i.e. ha una sola soluzione.
Quali sono i vantaggi del secondo metodo? Il vantaggio principale è la sua versatilità. Non ci interessa affatto se la matrice del sistema è quadrata o meno. Inoltre, abbiamo effettivamente effettuato trasformazioni dell'andamento in avanti del metodo di Gauss. Sono rimaste solo un paio di azioni e potremmo ottenere la soluzione di questo SLAE. A dire il vero, il secondo metodo mi piace più del primo, ma la scelta è una questione di gusti.
Risposta: Il dato SLAE è coerente e definito.
Esempio n. 2
Esplora SLAE $ \ left \ (\ begin (allineato) & x_1-x_2 + 2x_3 = -1; \\ & -x_1 + 2x_2-3x_3 = 3; \\ & 2x_1-x_2 + 3x_3 = 2; \\ & 3x_1- 2x_2 + 5x_3 = 1; \\ & 2x_1-3x_2 + 5x_3 = -4. \ Fine (allineato) \ a destra $ Per compatibilità.
Troveremo i ranghi della matrice del sistema e della matrice estesa del sistema con il metodo delle trasformazioni elementari. Matrice di sistema estesa: $ \ widetilde (A) = \ left (\ begin (array) (ccc | c) 1 & -1 & 2 & -1 \\ -1 & 2 & -3 & 3 \\ 2 & -1 & 3 & 2 \\ 3 & -2 & 5 & 1 \\ 2 & -3 & 5 & -4 \ fine (matrice) \ destra) $. Trova i ranghi richiesti trasformando la matrice estesa del sistema:
$$ \ left (\ begin (array) (ccc | c) 1 & -1 & 2 & -1 \\ -1 & 2 & -3 & 3 \\ 2 & -3 & 5 & -4 \\ 3 & -2 & 5 & 1 \\ 2 & -1 & 3 & 2 \ fine (matrice) \ destra) \ inizio (matrice) (l) \ fantasma (0) \\ r_2 + r_1 \\ r_3-2r_1 \\ r_4 -3r_1 \\ r_5-2r_1 \ fine (matrice) \ freccia destra \ sinistra (\ inizio (matrice) (ccc | c) 1 & -1 & 2 & -1 \\ 0 & 1 & -1 & 2 \\ 0 & -1 & 1 & -2 \\ 0 & 1 & -1 & 4 \\ 0 & 1 & -1 & 4 \ fine (matrice) \ destra) \ inizio (matrice) (l) \ fantasma (0) \\ \ phantom (0) \\ r_3-r_2 \\ r_4-r_2 \\ r_5 + r_2 \ end (array) \ rightarrow \\ $$ $$ \ rightarrow \ left (\ begin (array) (ccc | c) 1 & -1 & 2 & -1 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \ fine (matrice) \ destra) \ inizio (matrice) (l) \ fantasma (0) \\\ fantasma (0) \\\ fantasma (0) \\ r_4-r_3 \\\ fantasma (0) \ fine (matrice) \ freccia destra \ sinistra (\ begin (array) (ccc | c) 1 & -1 & 2 & -1 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \ fine (matrice) \ destra) $$
La matrice di sistema espansa viene scalata. Il rango di una matrice a gradini è uguale al numero delle sue righe diverse da zero, quindi $ \ rang \ widetilde (A) = 3 $. Anche la matrice $ A $ (al punto) è ridotta a una forma a gradini e il suo rango è 2, $ \ rang (A) = 2 $.
Poiché $ \ rang A \ neq \ rang \ widetilde (A) $, secondo il teorema di Kronecker-Capelli, il sistema è inconsistente (cioè non ha soluzioni).
Risposta: Il sistema è incoerente.
Esempio n. 3
Esplora SLAE $ \ left \ (\ begin (allineato) & 2x_1 + 7x_3-5x_4 + 11x_5 = 42; \\ & x_1-2x_2 + 3x_3 + 2x_5 = 17; \\ & -3x_1 + 9x_2-11x_3-7x_5 = -64 ; \\ & -5x_1 + 17x_2-16x_3-5x_4-4x_5 = -90; \\ & 7x_1-17x_2 + 23x_3 + 15x_5 = 132. \ Fine (allineato) \ destra. $ Per compatibilità.
Portiamo la matrice espansa del sistema in una forma graduale:
$$ \ left (\ begin (array) (ccccc | c) 2 & 0 & 7 & -5 & 11 & 42 \\ 1 & -2 & 3 & 0 & 2 & 17 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \ fine (matrice) \ destra) \ overset (r_1 \ leftrightarrow (r_3)) (\ rightarrow) $$ $$ \ rightarrow \ left (\ begin (array) (ccccc | c) 1 & -2 & 3 & 0 & 2 & 17 \\ 2 & 0 & 7 & -5 & 11 & 42 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \ end (array) \ right) \ begin (array) (l) \ phantom (0) \\ r_2-2r_1 \\ r_3 + 3r_1 \\ r_4 + 5r_1 \\ r_5-7r_1 \ end ( array) \ freccia destra \ sinistra (\ inizio (matrice) (ccccc | c) 1 & -2 & 3 & 0 & 2 & 17 \\ 0 & 4 & 1 & -5 & 7 & 8 \\ 0 & 3 & - 2 & 0 & -1 & -13 \\ 0 & 7 & -1 & -5 & 6 & -5 \\ 0 & -3 & 2 & 0 & 1 & 13 \ fine (matrice) \ destra) \ inizio ( array) (l) \ phantom (0) \\ \ phantom (0) \\ 4r_3 + 3r_2 \\ 4r_4-7r_2 \\ 4r_5 + 3r_2 \ end (array) \ rightarrow $$ \ rightarrow \ left (\ begin (array) ) (ccccc | c) 1 & -2 & 3 & 0 & 2 & 17 \\ 0 & 4 & 1 & -5 & 7 & 8 \\ 0 & 0 & -11 & 15 & -25 & -76 \\ 0 & 0 & -11 & 15 & -25 & -76 \\ 0 & 0 & 11 & -15 & 25 & 76 \ fine (matrice) \ destra) \ inizio (matrice) (l) \ fantasma (0) \\ \ fantasma (0) \\\ fantasma (0) \\ r_4 -r_3 \\ r_5 + r_2 \ end (array) \ rightarrow \ left (\ begin (array) (ccccc | c) 1 & -2 & 3 & 0 & 2 & 17 \\ 0 & 4 & 1 & -5 & 7 & 8 \\ 0 & 0 & -11 & 15 & -25 & -76 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \ fine (array) \ destra) $$
Abbiamo portato la matrice di sistema estesa e la matrice di sistema stessa a una forma a gradini. Il rango della matrice estesa del sistema è tre, anche il rango della matrice del sistema è tre. Poiché il sistema contiene $ n = 5 $ incognite, ad es. $ \ rang \ widetilde (A) = \ rang (A) \ lt (n) $, quindi, secondo il corollario del teorema di Kronecker-Capelli, questo sistema è indefinito, cioè ha un numero infinito di soluzioni.
Risposta: il sistema non è definito.
Nella seconda parte, analizzeremo esempi che sono spesso inclusi in calcoli o test tipici in matematica superiore: uno studio di compatibilità e la soluzione di uno SLAE, a seconda dei valori dei parametri inclusi in esso.
Esempio 1... Trova una soluzione generale e qualche soluzione particolare al sistemaSoluzione effettuiamo con l'aiuto di una calcolatrice. Scriviamo le matrici estese e di base: 
La linea tratteggiata separa la matrice principale A. Sopra scriviamo i sistemi incogniti, tenendo presente l'eventuale riarrangiamento dei termini nelle equazioni del sistema. Determinando il rango della matrice estesa, troviamo contemporaneamente il rango e quello principale. Nella matrice B, la prima e la seconda colonna sono proporzionali. Delle due colonne proporzionali, solo una può rientrare nel minore di base, quindi trasferiamo, ad esempio, la prima colonna dietro la linea tratteggiata con il segno opposto. Per il sistema, questo significa spostare i termini da x 1 al lato destro delle equazioni. 
Portiamo la matrice in una forma triangolare. Lavoreremo solo con righe, poiché moltiplicare una riga di una matrice per un numero diverso da zero e aggiungere un'altra riga per il sistema significa moltiplicare l'equazione per lo stesso numero e aggiungerla con un'altra equazione, che non cambia la soluzione di il sistema. Lavoriamo con la prima riga: moltiplichiamo la prima riga della matrice per (-3) e aggiungiamo a turno la seconda e la terza riga. Quindi moltiplichiamo la prima riga per (-2) e aggiungiamo alla quarta. 
La seconda e la terza riga sono proporzionali, quindi una di esse, ad esempio la seconda, può essere barrata. Ciò equivale a cancellare la seconda equazione del sistema, poiché è una conseguenza della terza. 
Ora stiamo lavorando con la seconda riga: moltiplicala per (-1) e aggiungila alla terza. 
Il minore tratteggiato ha l'ordine più alto (dei possibili minori) ed è diverso da zero (è uguale al prodotto degli elementi sulla diagonale principale), e questo minore appartiene sia alla matrice principale che a quella estesa, quindi rangA = rangB = 3.
Minore 
è fondamentale. Include i coefficienti per le incognite x 2, x 3, x 4, il che significa che le incognite x 2, x 3, x 4 sono dipendenti e x 1, x 5 sono libere.
Trasformiamo la matrice, lasciando a sinistra solo la base minore (che corrisponde al punto 4 dell'algoritmo di soluzione sopra). 
Il sistema con i coefficienti di questa matrice è equivalente al sistema originale e ha la forma
x 4 = 3-4x 5, x 3 = 3-4x 5 -2x 4 = 3-4x 5 -6 + 8x 5 = -3 + 4x 5
x 2 = x 3 + 2x 4 -2 + 2x 1 + 3x 5 = -3 + 4x 5 + 6-8x 5 -2 + 2x 1 + 3x 5 = 1 + 2x 1 -x 5
Abbiamo ottenuto i rapporti che esprimono le variabili dipendenti x 2, x 3, x 4 fino a x 1 e x 5 liberi, ovvero abbiamo trovato una soluzione generale:
Assegnando qualsiasi valore alle incognite libere, otteniamo un numero qualsiasi di soluzioni particolari. Troviamo due soluzioni particolari:
1) sia x 1 = x 5 = 0, quindi x 2 = 1, x 3 = -3, x 4 = 3;
2) metti x 1 = 1, x 5 = -1, quindi x 2 = 4, x 3 = -7, x 4 = 7.
Pertanto, abbiamo trovato due soluzioni: (0.1, -3.3.0) - una soluzione, (1.4, -7.7, -1) - un'altra soluzione.
Esempio 2... Indagare la compatibilità, trovare una soluzione generale e una particolare al sistema 
Soluzione... Riorganizziamo la prima e la seconda equazione in modo che abbiano unità nella prima equazione e scriviamo la matrice B. 
Otteniamo degli zeri nella quarta colonna, operando sulla prima riga: 
Ora otteniamo gli zeri nella terza colonna usando la seconda riga: 
La terza e la quarta riga sono proporzionali, quindi una di esse può essere cancellata senza modificare il rango:
Moltiplichiamo la terza riga per (-2) e aggiungiamo alla quarta: 
Vediamo che i ranghi delle matrici principale ed estesa sono uguali a 4 e il rango coincide con il numero di incognite, quindi il sistema ha un'unica soluzione:
-x 1 = -3 → x 1 = 3; x 2 = 3-x 1 → x 2 = 0; x 3 = 1-2 x 1 → x 3 = 5.
x 4 = 10 - 3x 1 - 3x 2 - 2x 3 = 11.
Esempio 3... Esaminare il sistema per verificarne la compatibilità e trovare una soluzione se esiste. 
Soluzione... Componiamo una matrice estesa del sistema. 
Riorganizziamo le prime due equazioni in modo che ci sia 1 nell'angolo in alto a sinistra:
Moltiplicando la prima riga per (-1), aggiungila alla terza: 
Moltiplica la seconda riga per (-2) e aggiungi alla terza: 
Il sistema è incoerente, poiché nella matrice principale abbiamo una riga composta da zeri, che viene cancellata quando viene trovato il rango, e nella matrice estesa rimarrà l'ultima riga, cioè r B> r A.
Esercizio... Indaga questo sistema di equazioni per verificarne la consistenza e risolvilo usando il calcolo matriciale.
Soluzione
Esempio... Dimostrare la compatibilità del sistema di equazioni lineari e risolverlo in due modi: 1) il metodo di Gauss; 2) Metodo di Cramer. (inserisci la risposta nella forma: x1, x2, x3)
Soluzione: doc: doc: xls
Risposta: 2,-1,3.
Esempio... Viene fornito un sistema di equazioni lineari. Dimostra la sua compatibilità. Trova una soluzione generale del sistema e una soluzione particolare.
Soluzione
Risposta: x 3 = - 1 + x 4 + x 5; x2 = 1 - x4; x 1 = 2 + x 4 - 3x 5
Esercizio... Trova soluzioni generali e specifiche per ogni sistema.
Soluzione. Indaghiamo questo sistema usando il teorema di Kronecker-Capelli.
Scriviamo le matrici estese e di base:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Qui la matrice A è in grassetto.
Portiamo la matrice in una forma triangolare. Lavoreremo solo con righe, poiché moltiplicare una riga di una matrice per un numero diverso da zero e aggiungere un'altra riga per il sistema significa moltiplicare l'equazione per lo stesso numero e aggiungerla con un'altra equazione, che non cambia la soluzione di il sistema.
Moltiplica la prima riga per (3). Moltiplica la 2a riga per (-1). Aggiungiamo la 2a riga alla 1a:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Moltiplica la seconda riga per (2). Moltiplica la 3a riga per (-3). Aggiungiamo la 3a riga alla 2a:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Moltiplica la 2a riga per (-1). Aggiungiamo la 2a riga alla 1a:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Il minore evidenziato ha l'ordine più alto (dei possibili minori) ed è diverso da zero (è uguale al prodotto degli elementi sulla diagonale inversa), e questo minore appartiene sia alla matrice principale che a quella estesa, quindi ha squillato ( A) = rang (B) = 3. Poiché il rango della matrice principale è uguale al rango della matrice estesa, allora il sistema è un giunto.
Questo minore è fondamentale. Include i coefficienti per le incognite x 1, x 2, x 3, il che significa che le incognite x 1, x 2, x 3 sono dipendenti (di base) e x 4, x 5 sono libere.
Trasformiamo la matrice, lasciando solo la base minore a sinistra.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
27x 3 =
- x 2 + 13 x 3 = - 1 + 3 x 4 - 6 x 5
2x 1 + 3x 2 - 3x 3 = 1 - 3x 4 + 2x 5
Utilizzando il metodo di eliminazione delle incognite, troviamo:
Abbiamo ottenuto relazioni che esprimono le variabili dipendenti x 1, x 2, x 3 fino a x 4, x 5 libere, cioè abbiamo trovato decisione comune:
x 3 = 0
x 2 = 1 - 3x 4 + 6x 5
x 1 = - 1 + 3x 4 - 8x 5
non definito da ha più di una soluzione.
Esercizio... Risolvi il sistema di equazioni.
Risposta: x 2 = 2 - 1,67 x 3 + 0,67 x 4
x 1 = 5 - 3,67 x 3 + 0,67 x 4
Assegnando qualsiasi valore alle incognite libere, otteniamo un numero qualsiasi di soluzioni particolari. Il sistema è non definito
