Základné elementárne funkcie, ich inherentné vlastnosti a príslušné grafy sú jedným zo základov matematických znalostí, podobne ako násobilka. Elementárne funkcie sú základom, podporou pre štúdium všetkých teoretických otázok.

Nižšie uvedený článok poskytuje kľúčový materiál na tému základných elementárnych funkcií. Zavedieme pojmy, dáme im definície; Pozrime sa podrobne na každý typ elementárnych funkcií a analyzujme ich vlastnosti.

Rozlišujú sa tieto typy základných elementárnych funkcií:

Definícia 1

• konštantná funkcia (konštantná);
• koreň n-tého stupňa;
• výkonová funkcia;
• exponenciálna funkcia;
• logaritmická funkcia;
• goniometrické funkcie;
• bratské goniometrické funkcie.

Konštantná funkcia je definovaná vzorcom: y = C (C je nejaké reálne číslo) a má aj názov: konštanta. Táto funkcia zisťuje, či nejaká reálna hodnota nezávisle premennej x zodpovedá rovnakej hodnote premennej y – hodnote C .

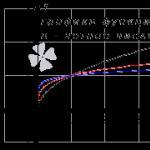
Graf konštanty je priamka, ktorá je rovnobežná s osou x a prechádza bodom so súradnicami (0, C). Pre názornosť uvádzame grafy konštantných funkcií y = 5, y = - 2, y = 3, y = 3 (na výkrese označené čiernou, červenou a modrou farbou).

Definícia 2

Táto elementárna funkcia je definovaná vzorcom y = x n (n je prirodzené číslo väčšie ako jedna).

Uvažujme o dvoch variantoch funkcie.

1. Odmocnina n-tého stupňa, n je párne číslo

Pre prehľadnosť uvádzame výkres, ktorý zobrazuje grafy takýchto funkcií: y = x, y = x 4 a y = x 8. Tieto funkcie sú farebne odlíšené: čierna, červená a modrá.

Podobný pohľad na grafy funkcie párneho stupňa pre iné hodnoty ukazovateľa.

Definícia 3

Vlastnosti koreňa funkcie n-tého stupňa, n je párne číslo

• definičný obor je množina všetkých nezáporných reálnych čísel [ 0 , + ∞) ;
• keď x = 0, funkcia y = x n má hodnotu rovnú nule;
• táto funkcia je funkciou všeobecného tvaru (nie je ani párna, ani nepárna);
• rozsah: [ 0 , + ∞) ;
• táto funkcia y = x n s párnymi exponentmi odmocniny narastá v celom definičnom obore;
• funkcia má konvexnosť so smerom nahor v celej oblasti definície;
• neexistujú žiadne inflexné body;
• nie sú žiadne asymptoty;
• graf funkcie pre párne n prechádza bodmi (0 ; 0) a (1 ; 1) .

1. Odmocnina n-tého stupňa, n je nepárne číslo

Takáto funkcia je definovaná na celej množine reálnych čísel. Pre prehľadnosť zvážte grafy funkcií y = x 3, y = x 5 a x 9. Na výkrese sú označené farbami: čierna, červená a modrá farba kriviek, resp.

Ostatné nepárne hodnoty exponentu koreňa funkcie y = x n poskytnú graf podobného tvaru.

Definícia 4

Vlastnosti koreňa funkcie n-tého stupňa, n je nepárne číslo

• definičný obor je množina všetkých reálnych čísel;
• táto funkcia je nepárna;
• rozsah hodnôt je množina všetkých reálnych čísel;
• funkcia y = x n s nepárnymi exponentmi odmocniny narastá v celom definičnom obore;
• funkcia má konkávnosť na intervale (- ∞ ; 0 ] a konvexnosť na intervale [ 0 , + ∞) ;
• inflexný bod má súradnice (0 ; 0) ;
• nie sú žiadne asymptoty;
• graf funkcie pre nepárne n prechádza bodmi (- 1 ; - 1) , (0 ; 0) a (1 ; 1) .

Funkcia napájania

Definícia 5

Mocninná funkcia je definovaná vzorcom y = x a .

Typ grafov a vlastnosti funkcie závisia od hodnoty exponentu.

• keď má mocninová funkcia celočíselný exponent a, potom tvar grafu mocninnej funkcie a jej vlastnosti závisia od toho, či je exponent párny alebo nepárny, a tiež aké znamienko má exponent. Uvažujme o všetkých týchto špeciálnych prípadoch podrobnejšie nižšie;
• exponent môže byť zlomkový alebo iracionálny - v závislosti od toho sa líši aj typ grafov a vlastnosti funkcie. Budeme analyzovať špeciálne prípady nastavením niekoľkých podmienok: 0< a < 1 ; a > 1 ; - 1 < a < 0 и a < - 1 ;
• mocninná funkcia môže mať nulový exponent, aj tento prípad rozoberieme podrobnejšie nižšie.

Poďme analyzovať výkonovú funkciu y = x a, keď a je nepárne kladné číslo, napríklad a = 1 , 3 , 5 …

Pre názornosť uvádzame grafy takýchto mocninových funkcií: y = x (čierna farba grafu), y = x 3 (modrá farba tabuľky), y = x 5 (červená farba grafu), y = x 7 (zelený graf). Keď a = 1, dostaneme lineárnu funkciu y = x.

Definícia 6

Vlastnosti mocninnej funkcie, keď je exponent nepárny kladný

• funkcia je rastúca pre x ∈ (- ∞ ; + ∞) ;
• funkcia je konvexná pre x ∈ (- ∞ ; 0 ] a konkávna pre x ∈ [ 0 ; + ∞) (okrem lineárnej funkcie);
• inflexný bod má súradnice (0 ; 0) (okrem lineárnej funkcie);
• nie sú žiadne asymptoty;
• body prechodu funkcie: (- 1 ; - 1) , (0 ; 0), (1 ; 1) .

Poďme analyzovať výkonovú funkciu y = x a, keď a je párne kladné číslo, napríklad a = 2 , 4 , 6 ...

Pre prehľadnosť uvádzame grafy takýchto výkonových funkcií: y \u003d x 2 (čierna farba grafu), y = x 4 (modrá farba grafu), y = x 8 (červená farba grafu). Keď a = 2, dostaneme kvadratickú funkciu, ktorej grafom je kvadratická parabola.

Definícia 7

Vlastnosti mocninovej funkcie, keď je exponent dokonca kladný:

• doména definície: x ∈ (- ∞ ; + ∞) ;
• klesajúce pre x ∈ (- ∞ ; 0 ] ;
• funkcia je konkávna pre x ∈ (- ∞ ; + ∞) ;
• neexistujú žiadne inflexné body;
• nie sú žiadne asymptoty;
• body prechodu funkcie: (- 1 ; 1) , (0 ; 0), (1 ; 1) .

Obrázok nižšie ukazuje príklady grafov exponenciálnych funkcií y = x a, keď a je nepárne záporné číslo: y = x - 9 (čierna farba grafu); y = x - 5 (modrá farba grafu); y = x - 3 (červená farba grafu); y = x - 1 (zelený graf). Keď a \u003d - 1, dostaneme inverznú úmernosť, ktorej graf je hyperbola.

Definícia 8

Vlastnosti mocninovej funkcie, keď je exponent nepárny záporný:

Keď x \u003d 0, dostaneme diskontinuitu druhého druhu, pretože lim x → 0 - 0 xa \u003d - ∞, lim x → 0 + 0 xa \u003d + ∞ pre \u003d - 1, - 3, - 5, .... Teda priamka x = 0 je vertikálna asymptota;

• rozsah: y ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• funkcia je nepárna, pretože y (- x) = - y (x) ;
• funkcia je klesajúca pre x ∈ - ∞ ; 0 ∪ (0 ; + ∞);
• funkcia je konvexná pre x ∈ (- ∞ ; 0) a konkávna pre x ∈ (0 ; + ∞) ;
• neexistujú žiadne inflexné body;

k = lim x → ∞ x a x = 0, b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0, keď a = - 1 , - 3 , - 5 , . . . .

• body prechodu funkcie: (- 1 ; - 1) , (1 ; 1) .

Obrázok nižšie ukazuje príklady grafov mocninných funkcií y = x a, keď a je párne záporné číslo: y = x - 8 (graf v čiernej farbe); y = x - 4 (modrá farba grafu); y = x - 2 (červená farba grafu).

Definícia 9

Vlastnosti mocninnej funkcie, keď je exponent dokonca záporný:

• doména definície: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;

Keď x \u003d 0, dostaneme diskontinuitu druhého druhu, pretože lim x → 0 - 0 xa \u003d + ∞, lim x → 0 + 0 xa \u003d + ∞ pre \u003d - 2, - 4, - 6, .... Teda priamka x = 0 je vertikálna asymptota;

• funkcia je párna, pretože y (- x) = y (x) ;
• funkcia je rastúca pre x ∈ (- ∞ ; 0) a klesajúca pre x ∈ 0 ; +∞;
• funkcia je konkávna pre x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• neexistujú žiadne inflexné body;
• horizontálna asymptota je priamka y = 0, pretože:

k = lim x → ∞ x a x = 0, b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0, keď a = - 2 , - 4 , - 6 , . . . .

• body prechodu funkcie: (- 1 ; 1) , (1 ; 1) .

Hneď na začiatku dbajte na nasledovné hľadisko: v prípade, že a je kladný zlomok s nepárnym menovateľom, niektorí autori berú ako definičný obor tejto mocninnej funkcie interval - ∞; + ∞ , pričom exponent a je neredukovateľný zlomok. V súčasnosti autori mnohých vzdelávacích publikácií o algebre a začiatkoch analýzy NEDEFINUJÚ mocninné funkcie, kde exponent je zlomok s nepárnym menovateľom pre záporné hodnoty argumentu. Ďalej sa budeme držať práve takejto polohy: vezmeme množinu [ 0 ; +∞). Odporúčanie pre žiakov: zistite si v tomto bode názor učiteľa, aby ste predišli nezhodám.

Poďme sa teda pozrieť na funkciu napájania y = x a, keď je exponentom racionálne alebo iracionálne číslo za predpokladu, že je 0< a < 1 .

Znázornime si pomocou grafov mocninné funkcie y = x a, keď a = 11 12 (graf v čiernej farbe); a = 5 7 (červená farba grafu); a = 1 3 (modrá farba grafu); a = 2 5 (zelená farba grafu).

Ostatné hodnoty exponentu a (za predpokladu 0< a < 1) дадут аналогичный вид графика.

Definícia 10

Vlastnosti mocninovej funkcie pri 0< a < 1:

• rozsah: y ∈ [ 0 ; +∞);
• funkcia je rastúca pre x ∈ [ 0 ; +∞);
• funkcia má konvexnosť pre x ∈ (0 ; + ∞) ;
• neexistujú žiadne inflexné body;
• nie sú žiadne asymptoty;

Poďme analyzovať výkonovú funkciu y = x a, keď exponent je necelé racionálne alebo iracionálne číslo za predpokladu, že a > 1 .

Znázorníme grafy mocninnej funkcie y \u003d xa za daných podmienok s použitím nasledujúcich funkcií ako príklad: y \u003d x 5 4, y \u003d x 4 3, y \u003d x 7 3, y \u003d x 3 π (čierna, červená, modrá, zelená grafy).

Ostatné hodnoty exponentu a pod podmienkou a > 1 poskytnú podobný pohľad na graf.

Definícia 11

Vlastnosti mocninovej funkcie pre a > 1:

• doména definície: x ∈ [ 0 ; +∞);
• rozsah: y ∈ [ 0 ; +∞);
• táto funkcia je funkciou všeobecného tvaru (nie je ani nepárna, ani párna);
• funkcia je rastúca pre x ∈ [ 0 ; +∞);
• funkcia je konkávna pre x ∈ (0 ; + ∞) (keď 1< a < 2) и выпуклость при x ∈ [ 0 ; + ∞) (когда a > 2);
• neexistujú žiadne inflexné body;
• nie sú žiadne asymptoty;
• body prechodu funkcie: (0 ; 0) , (1 ; 1) .

Upozorňujeme, že keď a je záporný zlomok s nepárnym menovateľom, v prácach niektorých autorov existuje názor, že doménou definície je v tomto prípade interval - ∞; 0 ∪ (0 ; + ∞) s podmienkou, že exponent a je neredukovateľný zlomok. V súčasnosti autori vzdelávacích materiálov o algebre a začiatkoch analýzy NEDEFINUJÚ mocninné funkcie s exponentom vo forme zlomku s nepárnym menovateľom pre záporné hodnoty argumentu. Ďalej sa držíme práve takého názoru: množinu (0 ; + ∞) berieme ako doménu mocninných funkcií so zlomkovými zápornými exponentmi. Návrh pre študentov: V tomto bode objasnite víziu svojho učiteľa, aby ste sa vyhli nezhodám.

Pokračujeme v téme a analyzujeme mocenskú funkciu y = x a za predpokladu: - 1< a < 0 .

Tu je nákres grafov nasledujúcich funkcií: y = x - 5 6 , y = x - 2 3 , y = x - 1 2 2 , y = x - 1 7 (čierne, červené, modré, zelené čiary, resp. ).

Definícia 12

Vlastnosti výkonovej funkcie pri - 1< a < 0:

lim x → 0 + 0 x a = + ∞ keď - 1< a < 0 , т.е. х = 0 – вертикальная асимптота;

• rozsah: y ∈ 0 ; +∞;
• táto funkcia je funkciou všeobecného tvaru (nie je ani nepárna, ani párna);
• neexistujú žiadne inflexné body;

Na obrázku nižšie sú znázornené grafy mocninných funkcií y = x - 5 4 , y = x - 5 3 , y = x - 6 , y = x - 24 7 (čierne, červené, modré, zelené farby kriviek).

Definícia 13

Vlastnosti výkonovej funkcie pre a< - 1:

• doména definície: x ∈ 0 ; +∞;

lim x → 0 + 0 x a = + ∞ keď a< - 1 , т.е. х = 0 – вертикальная асимптота;

• rozsah: y ∈ (0 ; + ∞) ;
• táto funkcia je funkciou všeobecného tvaru (nie je ani nepárna, ani párna);
• funkcia je klesajúca pre x ∈ 0; +∞;
• funkcia je konkávna pre x ∈ 0; +∞;
• neexistujú žiadne inflexné body;
• vodorovná asymptota - priamka y = 0 ;
• bod prechodu funkcie: (1 ; 1) .

Keď a \u003d 0 a x ≠ 0, dostaneme funkciu y \u003d x 0 \u003d 1, ktorá určuje čiaru, z ktorej je vylúčený bod (0; 1) (dohodli sme sa, že výraz 0 0 nebude daný akúkoľvek hodnotu).

Exponenciálna funkcia má tvar y = a x , kde a > 0 a a ≠ 1 a graf tejto funkcie vyzerá inak podľa hodnoty bázy a . Uvažujme o špeciálnych prípadoch.

Najprv analyzujme situáciu, keď má základ exponenciálnej funkcie hodnotu od nuly do jednej (0< a < 1) . Názorným príkladom sú grafy funkcií pre a = 1 2 (modrá farba krivky) a a = 5 6 (červená farba krivky).

Grafy exponenciálnej funkcie budú mať podobný tvar pre ostatné hodnoty základne za predpokladu, že 0< a < 1 .

Definícia 14

Vlastnosti exponenciálnej funkcie, keď je základňa menšia ako jedna:

• rozsah: y ∈ (0 ; + ∞) ;
• táto funkcia je funkciou všeobecného tvaru (nie je ani nepárna, ani párna);
• exponenciálna funkcia, ktorej základ je menší ako jedna, klesá v celom definičnom obore;
• neexistujú žiadne inflexné body;
• horizontálna asymptota je priamka y = 0 s premennou x smerujúcou k + ∞ ;

Teraz zvážte prípad, keď je základ exponenciálnej funkcie väčší ako jedna (a > 1).

Ilustrujme tento špeciálny prípad na grafe exponenciálnych funkcií y = 3 2 x (modrá farba krivky) a y = e x (červená farba grafu).

Ostatné hodnoty bázy, väčšie ako jedna, poskytnú podobný pohľad na graf exponenciálnej funkcie.

Definícia 15

Vlastnosti exponenciálnej funkcie, keď je základ väčší ako jedna:

• doménou definície je celá množina reálnych čísel;
• rozsah: y ∈ (0 ; + ∞) ;
• táto funkcia je funkciou všeobecného tvaru (nie je ani nepárna, ani párna);
• exponenciálna funkcia, ktorej základ je väčší ako jedna, je rastúca pre x ∈ - ∞ ; +∞;
• funkcia je konkávna pre x ∈ - ∞ ; +∞;
• neexistujú žiadne inflexné body;
• horizontálna asymptota - priamka y = 0 s premennou x smerujúcou k - ∞;
• bod prechodu funkcie: (0 ; 1) .

Logaritmická funkcia má tvar y = log a (x) , kde a > 0 , a ≠ 1 .

Takáto funkcia je definovaná iba pre kladné hodnoty argumentu: for x ∈ 0 ; +∞ .

Graf logaritmickej funkcie má rôznu formu podľa hodnoty základu a.

Najprv zvážte situáciu, keď 0< a < 1 . Продемонстрируем этот частный случай графиком логарифмической функции при a = 1 2 (синий цвет кривой) и а = 5 6 (красный цвет кривой).

Ostatné hodnoty základne, nie väčšie ako jedna, poskytnú podobný pohľad na graf.

Definícia 16

Vlastnosti logaritmickej funkcie, keď je základ menší ako jedna:

• doména definície: x ∈ 0 ; +∞ . Keďže x smeruje sprava k nule, hodnoty funkcie majú sklon k + ∞;
• rozsah: y ∈ - ∞ ; +∞;
• táto funkcia je funkciou všeobecného tvaru (nie je ani nepárna, ani párna);
• logaritmický
• funkcia je konkávna pre x ∈ 0; +∞;
• neexistujú žiadne inflexné body;
• nie sú žiadne asymptoty;

Teraz analyzujme špeciálny prípad, keď je základ logaritmickej funkcie väčší ako jedna: a > 1 . Na obrázku nižšie sú grafy logaritmických funkcií y = log 3 2 x a y = ln x (modrá a červená farba grafov).

Ostatné hodnoty základne väčšie ako jedna poskytnú podobný pohľad na graf.

Definícia 17

Vlastnosti logaritmickej funkcie, keď je základ väčší ako jedna:

• doména definície: x ∈ 0 ; +∞ . Keďže x smeruje sprava k nule, hodnoty funkcie majú sklon k - ∞;
• rozsah: y ∈ - ∞ ; + ∞ (celá množina reálnych čísel);
• táto funkcia je funkciou všeobecného tvaru (nie je ani nepárna, ani párna);
• logaritmická funkcia je rastúca pre x ∈ 0; +∞;
• funkcia má konvexnosť pre x ∈ 0; +∞;
• neexistujú žiadne inflexné body;
• nie sú žiadne asymptoty;
• bod prechodu funkcie: (1 ; 0) .

Goniometrické funkcie sú sínus, kosínus, tangens a kotangens. Poďme analyzovať vlastnosti každého z nich a príslušné grafy.

Vo všeobecnosti sa všetky goniometrické funkcie vyznačujú vlastnosťou periodicity, t.j. keď sa hodnoty funkcií opakujú pre rôzne hodnoty argumentu, ktoré sa navzájom líšia hodnotou periódy f (x + T) = f (x) (T je perióda). Do zoznamu vlastností goniometrických funkcií sa tak pridáva položka „najmenej kladné obdobie“. Okrem toho uvedieme také hodnoty argumentu, pre ktoré príslušná funkcia zmizne.

1. Sínusová funkcia: y = sin(x)

Graf tejto funkcie sa nazýva sínusová vlna.

Definícia 18

Vlastnosti funkcie sínus:

• doména definície: celá množina reálnych čísel x ∈ - ∞ ; +∞;
• funkcia zaniká, keď x = π k , kde k ∈ Z (Z je množina celých čísel);
• funkcia je rastúca pre x ∈ - π 2 + 2 π · k ; π 2 + 2 π k , k ∈ Z a klesajúce pre x ∈ π 2 + 2 π k ; 3 π 2 + 2 π k , k ∈ Z ;
• sínusová funkcia má lokálne maximá v bodoch π 2 + 2 π · k ; 1 a lokálne minimá v bodoch - π 2 + 2 π · k ; -1, k∈Z;
• funkcia sínus je konkávna, keď x ∈ - π + 2 π k; 2 π k , k ∈ Z a konvexné, keď x ∈ 2 π k ; π + 2 π k, k ∈ Z;
• nie sú žiadne asymptoty.

1. kosínusová funkcia: y=cos(x)

Graf tejto funkcie sa nazýva kosínusová vlna.

Definícia 19

Vlastnosti kosínusovej funkcie:

• doména definície: x ∈ - ∞ ; +∞;
• najmenšia kladná perióda: T \u003d 2 π;
• rozsah: y ∈ - 1; jeden ;
• táto funkcia je párna, pretože y (- x) = y (x) ;
• funkcia je rastúca pre x ∈ - π + 2 π · k ; 2 π · k , k ∈ Z a klesajúce pre x ∈ 2 π · k ; π + 2 π k, k ∈ Z;
• kosínusová funkcia má lokálne maximá v bodoch 2 π · k ; 1 , k ∈ Z a lokálne minimá v bodoch π + 2 π · k ; -1, k∈z;
• kosínusová funkcia je konkávna, keď x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π k, k ∈ Z a konvexné, keď x ∈ - π 2 + 2 π k ; π 2 + 2 π · k, k ∈ Z;
• inflexné body majú súradnice π 2 + π · k ; 0 , k ∈ Z
• nie sú žiadne asymptoty.

1. Funkcia dotyčnice: y = t g (x)

Graf tejto funkcie sa nazýva tangentoida.

Definícia 20

Vlastnosti funkcie dotyčnice:

• doména definície: x ∈ - π 2 + π · k ; π 2 + π k , kde k ∈ Z (Z je množina celých čísel);
• Správanie sa funkcie dotyčnice na hranici definičného oboru lim x → π 2 + π · k + 0 tg (x) = - ∞ , lim x → π 2 + π · k - 0 tg (x) = + ∞ . Čiary x = π 2 + π · k k ∈ Z sú teda vertikálne asymptoty;
• funkcia zanikne, keď x = π k pre k ∈ Z (Z je množina celých čísel);
• rozsah: y ∈ - ∞ ; +∞;
• táto funkcia je nepárna, pretože y (- x) = - y (x) ;
• funkcia je rastúca pri - π 2 + π · k ; π 2 + π k , k ∈ Z ;
• funkcia dotyčnice je pre x ∈ [ π · k konkávna; π 2 + π k), k ∈ Z a konvexné pre x ∈ (- π 2 + π k ; π k ] , k ∈ Z ;
• inflexné body majú súradnice π k; 0, k∈Z;

1. Funkcia kotangens: y = c t g (x)

Graf tejto funkcie sa nazýva kotangentoid. .

Definícia 21

Vlastnosti kotangens funkcie:

• doména definície: x ∈ (π k ; π + π k), kde k ∈ Z (Z je množina celých čísel);

Správanie funkcie kotangens na hranici definičného definičného oboru lim x → π · k + 0 t g (x) = + ∞ , lim x → π · k - 0 t g (x) = - ∞ . Čiary x = π k k ∈ Z sú teda zvislé asymptoty;

• najmenšia kladná perióda: T \u003d π;
• funkcia zanikne, keď x = π 2 + π k pre k ∈ Z (Z je množina celých čísel);
• rozsah: y ∈ - ∞ ; +∞;
• táto funkcia je nepárna, pretože y (- x) = - y (x) ;
• funkcia je klesajúca pre x ∈ π · k ; π + π k, k ∈ Z;
• funkcia kotangens je konkávna pre x ∈ (π k ; π 2 + π k ] , k ∈ Z a konvexná pre x ∈ [ - π 2 + π k ; π k), k ∈ Z ;
• inflexné body majú súradnice π 2 + π · k ; 0, k∈Z;
• neexistujú žiadne šikmé a horizontálne asymptoty.

Inverzné goniometrické funkcie sú arksínus, arkkozín, arktangens a arkkotangens. V dôsledku prítomnosti predpony „oblúk“ v názve sa inverzné goniometrické funkcie často nazývajú oblúkové funkcie. .

1. Funkcia Arcsine: y = a rc sin (x)

Definícia 22

Vlastnosti funkcie arcsínus:

• táto funkcia je nepárna, pretože y (- x) = - y (x) ;
• funkcia arcsínus je konkávna pre x ∈ 0; 1 a konvexnosť pre x ∈ - 1; 0;
• inflexné body majú súradnice (0 ; 0) , je to zároveň nula funkcie;
• nie sú žiadne asymptoty.

1. Funkcia Arcosine: y = a rc cos (x)

Definícia 23

Vlastnosti funkcie arkkozín:

• doména definície: x ∈ - 1 ; jeden ;
• rozsah: y ∈ 0 ; π;
• táto funkcia má všeobecnú formu (ani párna, ani nepárna);
• funkcia klesá na celom definičnom obore;
• funkcia arkkozínu je konkávna pre x ∈ - 1 ; 0 a konvexnosť pre x ∈ 0 ; jeden ;
• inflexné body majú súradnice 0 ; π2;
• nie sú žiadne asymptoty.

1. Arktangens funkcia: y = a r c t g (x)

Definícia 24

Vlastnosti funkcie arctangens:

• doména definície: x ∈ - ∞ ; +∞;
• rozsah: y ∈ - π 2 ; π2;
• táto funkcia je nepárna, pretože y (- x) = - y (x) ;
• funkcia sa zvyšuje v celej oblasti definície;
• funkcia arkustangens je konkávna pre x ∈ (- ∞ ; 0 ] a konvexná pre x ∈ [ 0 ; + ∞) ;
• inflexný bod má súradnice (0; 0), je zároveň nulou funkcie;
• vodorovné asymptoty sú priame čiary y = - π 2 pre x → - ∞ a y = π 2 pre x → + ∞ (asymptoty na obrázku sú zelené čiary).

1. Oblúková kotangens funkcia: y = a r c c t g (x)

Definícia 25

Vlastnosti funkcie kotangens oblúka:

• doména definície: x ∈ - ∞ ; +∞;
• rozsah: y ∈ (0 ; π) ;
• táto funkcia je všeobecného typu;
• funkcia klesá na celom definičnom obore;
• funkcia kotangens oblúka je konkávna pre x ∈ [ 0 ; + ∞) a konvexnosť pre x ∈ (- ∞ ; 0 ] ;
• inflexný bod má súradnice 0 ; π2;
• vodorovné asymptoty sú priame čiary y = π v bode x → - ∞ (zelená čiara na výkrese) a y = 0 v bode x → + ∞.

Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter

Dĺžka segmentu na súradnicovej osi sa zistí podľa vzorca:

Dĺžka segmentu v rovine súradníc sa hľadá podľa vzorca:

Na nájdenie dĺžky segmentu v trojrozmernom súradnicovom systéme sa používa nasledujúci vzorec:

Súradnice stredu segmentu (pre súradnicovú os sa používa iba prvý vzorec, pre rovinu súradníc - prvé dva vzorce, pre trojrozmerný súradnicový systém - všetky tri vzorce) sa vypočítajú podľa vzorcov:

Funkcia je zhoda s formulárom r= f(X) medzi premennými, vďaka čomu každá uvažovala o hodnote nejakej premennej X(argument alebo nezávislá premenná) zodpovedá určitej hodnote inej premennej, r(závislá premenná, niekedy sa táto hodnota nazýva jednoducho hodnota funkcie). Všimnite si, že funkcia predpokladá, že jedna hodnota argumentu X môže existovať iba jedna hodnota závislej premennej pri. Avšak rovnakú hodnotu pri možno získať s rôznymi X.

Rozsah funkcie sú všetky hodnoty nezávislej premennej (argument funkcie, zvyčajne X) pre ktorý je funkcia definovaná, t.j. jeho význam existuje. Je uvedená doména definície D(r). Celkovo tento pojem už poznáte. Rozsah funkcie sa inak nazýva doména platných hodnôt alebo ODZ, ktorú ste už dlho vedeli nájsť.

Funkčný rozsah sú všetky možné hodnoty závislej premennej tejto funkcie. Označené E(pri).

Funkcia stúpa na intervale, na ktorom väčšia hodnota argumentu zodpovedá väčšej hodnote funkcie. Funkcia klesá na intervale, na ktorom väčšia hodnota argumentu zodpovedá menšej hodnote funkcie.

Funkčné intervaly sú intervaly nezávislej premennej, v ktorých si závislá premenná zachováva svoje kladné alebo záporné znamienko.

Funkčné nuly sú tie hodnoty argumentu, pre ktoré je hodnota funkcie rovná nule. V týchto bodoch graf funkcie pretína os x (os OX). Potreba nájsť nuly funkcie veľmi často znamená jednoduché riešenie rovnice. Potreba nájsť intervaly stálosti tiež často znamená potrebu jednoducho vyriešiť nerovnosť.

Funkcia r = f(X) sa volajú dokonca X

To znamená, že pre akékoľvek opačné hodnoty argumentu sú hodnoty párnej funkcie rovnaké. Graf párnej funkcie je vždy symetrický okolo osi y operačného zosilňovača.

Funkcia r = f(X) sa volajú zvláštny, ak je definovaný na symetrickej množine a pre ľubovoľnú X z oblasti definície je splnená rovnosť:

To znamená, že pre akékoľvek opačné hodnoty argumentu sú hodnoty nepárnej funkcie tiež opačné. Graf nepárnej funkcie je vždy symetrický podľa počiatku.

Súčet koreňov párnych a nepárnych funkcií (priesečníkov osi x OX) sa vždy rovná nule, pretože za každý kladný koreň X má negatívny koreň X.

Je dôležité poznamenať, že niektoré funkcie nemusia byť párne alebo nepárne. Existuje veľa funkcií, ktoré nie sú ani párne, ani nepárne. Takéto funkcie sú tzv všeobecné funkcie a neplatí pre nich žiadna z vyššie uvedených rovností alebo vlastností.

Lineárna funkcia sa nazýva funkcia, ktorá môže byť daná vzorcom:

Graf lineárnej funkcie je priamka a vo všeobecnom prípade vyzerá takto (uvádzame príklad pre prípad, keď k> 0, v tomto prípade je funkcia rastúca; pre prípad k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону - слева направо):

Graf kvadratickej funkcie (Parabola)

Graf paraboly je daný kvadratickou funkciou:

Kvadratická funkcia, ako každá iná funkcia, pretína os OX v bodoch, ktoré sú jej koreňmi: ( X jeden ; 0) a ( X 2; 0). Ak neexistujú žiadne korene, potom kvadratická funkcia nepretína os OX, ak existuje jeden koreň, potom v tomto bode ( X 0; 0) kvadratická funkcia sa iba dotýka osi OX, ale nepretína ju. Kvadratická funkcia vždy pretína os OY v bode so súradnicami: (0; c). Graf kvadratickej funkcie (paraboly) môže vyzerať takto (obrázok ukazuje príklady, ktoré zďaleka nevyčerpávajú všetky možné typy parabol):

kde:

• ak koeficient a> 0, vo funkcii r = sekera 2 + bx + c, potom sú vetvy paraboly nasmerované nahor;
• ak a < 0, то ветви параболы направлены вниз.

Súradnice vrcholov paraboly možno vypočítať pomocou nasledujúcich vzorcov. X topy (p- na obrázkoch vyššie) paraboly (alebo bodu, v ktorom štvorcová trojčlenka dosiahne svoju maximálnu alebo minimálnu hodnotu):

Y topy (q- na obrázkoch vyššie) paraboly alebo maximálne, ak vetvy paraboly smerujú nadol ( a < 0), либо минимальное, если ветви параболы направлены вверх (a> 0), hodnota štvorcového trinomu:

Grafy iných funkcií

výkonová funkcia

Tu je niekoľko príkladov grafov mocninových funkcií:

Nepriamo úmerná závislosť zavolajte funkciu danú vzorcom:

V závislosti od znamienka čísla k Nepriamo úmerný graf môže mať dve základné možnosti:

Asymptota je priamka, ku ktorej sa priamka grafu funkcie nekonečne blízko približuje, ale nepretína sa. Asymptoty pre grafy inverznej úmernosti znázornené na obrázku vyššie sú súradnicové osi, ku ktorým sa graf funkcie nekonečne blízko približuje, ale nepretína ich.

exponenciálna funkcia so základňou a zavolajte funkciu danú vzorcom:

a graf exponenciálnej funkcie môže mať dve základné možnosti (uvedieme aj príklady, pozri nižšie):

logaritmická funkcia zavolajte funkciu danú vzorcom:

Podľa toho, či je číslo väčšie alebo menšie ako jedna a Graf logaritmickej funkcie môže mať dve základné možnosti:

Graf funkcií r = |X| nasledovne:

Grafy periodických (trigonometrických) funkcií

Funkcia pri = f(X) sa nazýva periodikum, ak takéto nenulové číslo existuje T, čo f(X + T) = f(X), pre hocikoho X mimo rozsahu funkcie f(X). Ak je funkcia f(X) je periodické s bodkou T, potom funkcia:

kde: A, k, b sú konštantné čísla a k nerovná sa nule, tiež periodické s bodkou T 1, ktorý je určený vzorcom:

Väčšina príkladov periodických funkcií sú goniometrické funkcie. Tu sú grafy hlavných goniometrických funkcií. Nasledujúci obrázok znázorňuje časť grafu funkcie r= hriech X(celý graf pokračuje nekonečne doľava a doprava), graf funkcie r= hriech X volal sínusoida:

Graf funkcií r= čos X volal kosínusová vlna. Tento graf je znázornený na nasledujúcom obrázku. Od grafu sínusu pokračuje donekonečna pozdĺž osi OX doľava a doprava:

Graf funkcií r=tg X volal tangentoida. Tento graf je znázornený na nasledujúcom obrázku. Rovnako ako grafy iných periodických funkcií, aj tento graf sa donekonečna opakuje pozdĺž osi OX doľava a doprava.

A nakoniec graf funkcie r=ctg X volal kotangentoid. Tento graf je znázornený na nasledujúcom obrázku. Rovnako ako grafy iných periodických a goniometrických funkcií, aj tento graf sa donekonečna opakuje pozdĺž osi OX doľava a doprava.

• späť
• Vpred

Ako sa úspešne pripraviť na CT z fyziky a matematiky?

Pre úspešnú prípravu na CT z fyziky a matematiky musia byť okrem iného splnené tri kritické podmienky:

1. Preštudujte si všetky témy a vyplňte všetky testy a úlohy uvedené v študijných materiáloch na tejto stránke. Nepotrebujete k tomu vôbec nič, a to: venovať sa každý deň tri až štyri hodiny príprave na CT z fyziky a matematiky, štúdiu teórie a riešeniu úloh. Faktom je, že DT je ​​skúška, pri ktorej nestačí vedieť len fyziku či matematiku, ale treba vedieť rýchlo a bez neúspechov vyriešiť veľké množstvo problémov na rôzne témy a rôznej zložitosti. To posledné sa dá naučiť len riešením tisícok problémov.
2. Naučte sa všetky vzorce a zákony vo fyzike a vzorce a metódy v matematike. V skutočnosti je to tiež veľmi jednoduché, vo fyzike je len asi 200 potrebných vzorcov a v matematike ešte o niečo menej. V každom z týchto predmetov je asi tucet štandardných metód na riešenie problémov základnej úrovne zložitosti, ktoré sa možno aj naučiť, a tak úplne automaticky a bez problémov vyriešiť väčšinu digitálnej transformácie v správnom čase. Potom už budete musieť myslieť len na tie najťažšie úlohy.
3. Zúčastnite sa všetkých troch stupňov skúšobného testovania z fyziky a matematiky. Každý RT je možné navštíviť dvakrát, aby sa vyriešili obe možnosti. Opäť platí, že na DT je ​​okrem schopnosti rýchlo a efektívne riešiť problémy a znalosti vzorcov a metód potrebné aj vedieť správne plánovať čas, rozložiť sily a hlavne správne vyplniť odpoveďový formulár, bez toho, aby ste si pomýlili čísla odpovedí a problémov alebo svoje vlastné meno. Taktiež je počas RT dôležité zvyknúť si na štýl kladenia otázok v úlohách, ktorý sa môže nepripravenému človeku na DT zdať veľmi nezvyčajný.

Úspešná, usilovná a zodpovedná implementácia týchto troch bodov, ako aj zodpovedné štúdium záverečných tréningových testov vám umožní ukázať na CT vynikajúci výsledok, maximum toho, čoho ste schopní.

Našli ste chybu?

Ak ste, ako sa vám zdá, našli chybu v školiacich materiáloch, napíšte o nej e-mailom (). V liste uveďte predmet (fyziku alebo matematiku), názov alebo číslo témy alebo testu, číslo úlohy, prípadne miesto v texte (strane), kde je podľa vás chyba. Popíšte aj údajnú chybu. Váš list nezostane bez povšimnutia, chyba bude buď opravená, alebo vám bude vysvetlené, prečo nejde o chybu.

Pozrime sa, ako preskúmať funkciu pomocou grafu. Ukazuje sa, že pri pohľade na graf môžete zistiť všetko, čo nás zaujíma, a to:

• rozsah funkcie
• funkčný rozsah
• funkčné nuly
• obdobia nárastu a poklesu
• vysoké a nízke body
• najväčšia a najmenšia hodnota funkcie na segmente.

Ujasnime si terminológiu:

Abscisa je horizontálna súradnica bodu.
Ordinovať- vertikálna súradnica.
úsečka- vodorovná os, najčastejšie nazývaná os.
Os Y- vertikálna os, alebo os.

Argumentovať je nezávislá premenná, od ktorej závisia hodnoty funkcie. Najčastejšie indikované.
Inými slovami, sami si vyberieme , dosadíme vo funkčnom vzorci a dostaneme .

doména funkcie - množina tých (a iba tých) hodnôt argumentu, pre ktoré funkcia existuje.
Označené: alebo .

Na našom obrázku je doménou funkcie segment. Práve na tomto segmente je nakreslený graf funkcie. Táto funkcia existuje iba tu.

Funkčný rozsah je množina hodnôt, ktoré premenná nadobúda. Na našom obrázku ide o segment – ​​od najnižšej po najvyššiu hodnotu.

Funkčné nuly- body, kde sa hodnota funkcie rovná nule, t.j. Na našom obrázku sú to body a .

Funkčné hodnoty sú kladné kde . Na našom obrázku sú to intervaly a .
Funkčné hodnoty sú záporné kde . Tento interval (alebo interval) máme od do.

Najdôležitejšie pojmy - zvyšovanie a znižovanie funkcií na nejakej zostave. Ako množinu môžete vziať segment, interval, spojenie intervalov alebo celú číselnú os.

Funkcia zvyšuje

Inými slovami, čím viac, tým viac, to znamená, že graf ide doprava a nahor.

Funkcia klesajúci na množine ak pre nejaké a patriace do množiny nerovnosť implikuje nerovnosť .

Pre klesajúcu funkciu väčšia hodnota zodpovedá menšej hodnote. Graf ide doprava a dole.

V našom obrázku sa funkcia zvyšuje na intervale a klesá na intervaloch a .

Definujme, čo je maximálne a minimálne body funkcie.

Maximálny bod- toto je vnútorný bod definičného oboru, takže hodnota funkcie v ňom je väčšia ako vo všetkých bodoch dostatočne blízko k nemu.
Inými slovami, maximálny bod je taký bod, hodnota funkcie, pri ktorej viac ako v susedných. Toto je miestny "kopec" na mape.

Na našom obrázku - maximálny bod.

Nízky bod- vnútorný bod definičného oboru, takže hodnota funkcie v ňom je menšia ako vo všetkých bodoch dostatočne blízko k nemu.
To znamená, že minimálny bod je taký, že hodnota funkcie v ňom je menšia ako v susedných. Na grafe ide o miestnu „dieru“.

Na našom obrázku - minimálny bod.

Pointa je hranica. Nie je to vnútorný bod domény definície, a preto nezodpovedá definícii maximálneho bodu. Veď ona nemá susedov vľavo. Rovnako tak na našom grafe nemôže byť žiadny minimálny bod.

Maximálny a minimálny počet bodov sa nazývajú spoločne extrémne body funkcie. V našom prípade je to a .

Čo ak však potrebujete nájsť napr. funkčné minimum na reze? V tomto prípade je odpoveď: pretože funkčné minimum je jeho hodnota v minimálnom bode.

Podobne maximum našej funkcie je . Dosiahne sa v bode .

Dá sa povedať, že extrémy funkcie sa rovnajú a .

Niekedy v úlohách musíte nájsť najväčšie a najmenšie hodnoty funkcie v danom segmente. Nemusia sa nevyhnutne zhodovať s extrémami.

V našom prípade najmenšia funkčná hodnota na intervale sa rovná minimu funkcie a zhoduje sa s ním. Ale jeho najväčšia hodnota v tomto segmente sa rovná . Dosahuje sa na ľavom konci segmentu.

V každom prípade sa najväčšie a najmenšie hodnoty spojitej funkcie na segmente dosahujú buď v extrémnych bodoch, alebo na koncoch segmentu.

Tento metodický materiál je len orientačný a pokrýva široké spektrum tém. Článok poskytuje prehľad grafov hlavných elementárnych funkcií a zaoberá sa najdôležitejšou otázkou - ako správne a RÝCHLO zostaviť graf. V priebehu štúdia vyššej matematiky bez znalosti grafov základných elementárnych funkcií to bude ťažké, preto je veľmi dôležité zapamätať si, ako vyzerajú grafy paraboly, hyperboly, sínusu, kosínusu atď., zapamätať si niektoré funkčné hodnoty. Povieme si aj o niektorých vlastnostiach hlavných funkcií.

Nepredstieram úplné a vedecky dôkladné materiály, dôraz sa bude klásť predovšetkým na prax - tie veci, s ktorými človek musí čeliť doslova na každom kroku, v akejkoľvek téme vyššej matematiky. Tabuľky pre figuríny? Dá sa to povedať.

Na základe dopytu čitateľov klikateľný obsah:

Okrem toho je k téme ultrakrátky abstrakt
– ovládnite 16 typov grafov štúdiom ŠESŤ strán!

Vážne, šesť, aj ja sám som bol prekvapený. Tento abstrakt obsahuje vylepšenú grafiku a je k dispozícii za symbolický poplatok, môžete si pozrieť demo verziu. Súbor je vhodné vytlačiť, aby ste mali grafy vždy po ruke. Ďakujeme za podporu projektu!

A hneď začíname:

Ako správne zostaviť súradnicové osi?

V praxi testy takmer vždy vypracúvajú žiaci do samostatných zošitov, vyskladaných v klietke. Prečo potrebujete kockované označenie? Koniec koncov, prácu je možné v zásade vykonať na listoch A4. A klietka je potrebná práve pre kvalitný a presný dizajn výkresov.

Akékoľvek kreslenie funkčného grafu začína súradnicovými osami.

Výkresy sú dvojrozmerné a trojrozmerné.

Uvažujme najskôr o dvojrozmernom prípade Kartézsky súradnicový systém:

1) Nakreslíme súradnicové osi. Os je tzv os x a os os y . Vždy sa ich snažíme nakresliť úhľadné a nie krivé. Šípky by tiež nemali pripomínať bradu Papa Carla.

2) Osy podpisujeme veľkými písmenami „x“ a „y“. Nezabudnite podpísať osy.

3) Nastavte mierku pozdĺž osí: nakreslite nulu a dve jednotky. Pri vytváraní výkresu je najpohodlnejšia a najbežnejšia mierka: 1 jednotka = 2 bunky (výkres vľavo) - ak je to možné, držte sa. Z času na čas sa však stane, že sa nám kresba nezmestí na hárok zošita – vtedy zmenšíme mierku: 1 jednotka = 1 bunka (výkres vpravo). Zriedkavo, ale stáva sa, že mierka kresby sa musí ešte viac zmenšiť (alebo zväčšiť).

NEČMÁHAJTE zo samopalu ... -5, -4, -3, -1, 0, 1, 2, 3, 4, 5, .... Súradnicová rovina totiž nie je Descartovým pomníkom a študent nie je holubica. Dali sme nula a dve jednotky pozdĺž osí. Niekedy namiesto jednotiek, je vhodné „detekovať“ iné hodnoty, napríklad „dva“ na osi x a „tri“ na osi y - a tento systém (0, 2 a 3) tiež jednoznačne nastaví súradnicovú sieť.

Odhadované rozmery výkresu je lepšie odhadnúť PRED kreslením výkresu.. Ak teda úloha vyžaduje napríklad nakreslenie trojuholníka s vrcholmi , , , potom je celkom jasné, že populárna mierka 1 jednotka = 2 bunky nebude fungovať. prečo? Pozrime sa na vec - tu musíte merať pätnásť centimetrov a kresba sa, samozrejme, nezmestí (alebo sa sotva zmestí) na list zošita. Preto hneď vyberieme menšiu mierku 1 jednotka = 1 bunka.

Mimochodom, asi centimetre a bunky notebooku. Je pravda, že v 30 bunkách notebooku je 15 centimetrov? Odmerajte si v zošite pre zaujímavosť pravítkom 15 centimetrov. V ZSSR to možno bola pravda... Je zaujímavé poznamenať, že ak zmeriate rovnaké centimetre vodorovne a zvisle, výsledky (v bunkách) budú iné! Prísne vzaté, moderné notebooky nie sú kockované, ale obdĺžnikové. Môže sa to zdať ako nezmysel, ale kresliť napríklad kružnicu kružidlom v takýchto situáciách je veľmi nepohodlné. Úprimne povedané, v takých chvíľach začínate uvažovať o správnosti súdruha Stalina, ktorého poslali do táborov na hackerské práce vo výrobe, nehovoriac o domácom automobilovom priemysle, padajúcich lietadlách či vybuchujúcich elektrárňach.

Keď už hovoríme o kvalite, alebo krátke odporúčanie na písacie potreby. K dnešnému dňu je väčšina notebookov v predaji, bez toho, aby sme povedali zlé slová, úplne škriatkovia. Z toho dôvodu, že sa namočia, a to nielen z gélových pier, ale aj z guľôčkových pier! Ušetrite na papieri. Na návrh testov odporúčam použiť notebooky Arkhangelskej celulózky a papiera (18 listov, bunka) alebo Pyaterochka, aj keď je to drahšie. Vhodné je zvoliť gélové pero, aj tá najlacnejšia čínska gélová náplň je oveľa lepšia ako guľôčkové pero, ktoré papier buď rozmazáva, alebo trhá. Jediné "konkurenčné" guľôčkové pero v mojej pamäti je Erich Krause. Píše zreteľne, krásne a stabilne – buď s plnou, alebo takmer prázdnou.

Okrem toho: Vízia pravouhlého súradnicového systému očami analytickej geometrie je zahrnutá v článku Lineárna (ne)závislosť vektorov. Vektorový základ, podrobné informácie o súradnicových štvrťrokoch nájdete v druhom odseku lekcie Lineárne nerovnosti.

3D puzdro

Tu je to skoro rovnaké.

1) Nakreslíme súradnicové osi. štandard: os aplikácie – smeruje nahor, os – smeruje doprava, os – smerom dole doľava prísne pod uhlom 45 stupňov.

2) Podpíšeme osi.

3) Nastavte mierku pozdĺž osí. Mierka pozdĺž osi - dvakrát menšia ako mierka pozdĺž ostatných osí. Všimnite si tiež, že v pravom výkrese som použil neštandardný "serif" pozdĺž osi (táto možnosť už bola spomenutá vyššie). Z môjho pohľadu je to presnejšie, rýchlejšie a estetickejšie – netreba hľadať stred bunky pod mikroskopom a „vyrezávať“ jednotku až po počiatok.

Pri opätovnom 3D kreslení dávajte prednosť mierke
1 jednotka = 2 bunky (nákres vľavo).

Načo sú všetky tieto pravidlá? Pravidlá sú na to, aby sa porušovali. Čo budem teraz robiť. Faktom je, že následné kresby článku urobím ja v Exceli a súradnicové osi budú vyzerať nesprávne z hľadiska správneho návrhu. Všetky grafy by som mohol kresliť ručne, ale kresliť ich je naozaj strašidelné, pretože Excel sa zdráha kresliť ich oveľa presnejšie.

Grafy a základné vlastnosti elementárnych funkcií

Lineárna funkcia je daná rovnicou . Graf lineárnej funkcie je priamy. Na zostrojenie priamky stačí poznať dva body.

Príklad 1

Nakreslite funkciu. Nájdime dva body. Ako jeden z bodov je výhodné zvoliť nulu.

Ak potom

Zoberme si nejaký iný bod, napríklad 1.

Ak potom

Pri príprave úloh sú súradnice bodov zvyčajne zhrnuté v tabuľke:

A samotné hodnoty sa počítajú ústne alebo na koncepte, kalkulačke.

Našli sme dva body, poďme nakresliť:

Pri kreslení výkresu vždy podpisujeme grafiku.

Nebude zbytočné pripomínať špeciálne prípady lineárnej funkcie:

Všimnite si, ako som umiestnil titulky, podpisy by pri štúdiu výkresu nemali byť nejednoznačné. V tomto prípade bolo veľmi nežiaduce umiestniť podpis vedľa priesečníka čiar alebo vpravo dole medzi grafy.

1) Lineárna funkcia tvaru () sa nazýva priama úmernosť. Napríklad . Graf priamej úmernosti vždy prechádza počiatkom. Konštrukcia priamky je teda zjednodušená – stačí nájsť len jeden bod.

2) Rovnica v tvare vymedzuje priamku rovnobežnú s osou, najmä samotná os je daná rovnicou. Graf funkcie je zostavený okamžite, bez nájdenia akýchkoľvek bodov. To znamená, že záznam treba chápať takto: "y sa vždy rovná -4 pre akúkoľvek hodnotu x."

3) Rovnica v tvare definuje priamku rovnobežnú s osou, konkrétne os samotná je daná rovnicou. Okamžite sa zostaví aj graf funkcie. Záznam by sa mal chápať takto: "x sa vždy pre akúkoľvek hodnotu y rovná 1."

Niektorí sa budú pýtať, no, prečo si spomínať na 6. ročník?! Je to tak, možno je to tak, len za roky praxe som stretol dobrý tucet študentov, ktorí boli zmätení úlohou zostrojiť graf ako alebo .

Kreslenie rovnej čiary je najbežnejšou činnosťou pri vytváraní výkresov.

Priamka je podrobne diskutovaná v kurze analytickej geometrie a kto chce, môže si prečítať článok Rovnica priamky na rovine.

Graf kvadratickej funkcie, graf kubickej funkcie, graf polynómu

Parabola. Graf kvadratickej funkcie () je parabola. Zvážte slávny prípad:

Pripomeňme si niektoré vlastnosti funkcie.

Takže riešenie našej rovnice: - v tomto bode sa nachádza vrchol paraboly. Prečo je to tak, sa dozviete z teoretického článku o derivácii a lekcie o extrémoch funkcie. Medzitým vypočítame zodpovedajúcu hodnotu "y":

Takže vrchol je v bode

Teraz nájdeme ďalšie body, pričom drzo využívame symetriu paraboly. Treba poznamenať, že funkcia – nie je rovnomerné, ale napriek tomu nikto nezrušil symetriu paraboly.

V akom poradí nájsť zvyšné body, myslím, že bude jasné z konečnej tabuľky:

Tento konštrukčný algoritmus možno obrazne nazvať „kyvadlo“ alebo princíp „tam a späť“ s Anfisou Čechovou.

Urobme si kresbu:

Z uvažovaných grafov prichádza na myseľ ďalšia užitočná funkcia:

Pre kvadratickú funkciu () platí:

Ak , potom vetvy paraboly smerujú nahor.

Ak , potom vetvy paraboly smerujú nadol.

Hlbokú znalosť krivky je možné získať na lekcii Hyperbola a parabola.

Kubická parabola je daná funkciou . Tu je kresba známa zo školy:

Uvádzame hlavné vlastnosti funkcie

Graf funkcií

Predstavuje jednu z vetiev paraboly. Urobme si kresbu:

Hlavné vlastnosti funkcie:

V tomto prípade je os vertikálna asymptota pre graf hyperboly na .

VEĽKOU chybou bude, ak pri kreslení z nedbanlivosti dovolíte, aby sa graf pretínal s asymptotou.

Také jednostranné limity, povedzte nám, že hyperbola nie je zhora obmedzený a nie je obmedzený zdola.

Poďme preskúmať funkciu v nekonečne: , to znamená, že ak sa začneme pohybovať pozdĺž osi doľava (alebo doprava) do nekonečna, potom budú „hry“ štíhlym krokom. nekonečne blízko priblížiť sa k nule a podľa toho aj vetvy hyperboly nekonečne blízko priblížiť sa k osi.

Takže os je horizontálna asymptota pre graf funkcie, ak "x" smeruje k plus alebo mínus nekonečnu.

Funkcia je zvláštny, čo znamená, že hyperbola je symetrická vzhľadom na pôvod. Táto skutočnosť je zrejmá z výkresu, navyše sa dá ľahko analyticky overiť: .

Graf funkcie tvaru () predstavuje dve vetvy hyperboly.

Ak , potom sa hyperbola nachádza v prvom a treťom súradnicovom kvadrante(pozri obrázok vyššie).

Ak , potom sa hyperbola nachádza v druhom a štvrtom súradnicovom kvadrante.

Analyzovať špecifikovanú pravidelnosť miesta pobytu hyperboly z pohľadu geometrických transformácií grafov nie je ťažké.

Príklad 3

Zostrojte pravú vetvu hyperboly

Používame metódu bodovej konštrukcie, pričom je výhodné voliť hodnoty tak, aby sa delili úplne:

Urobme si kresbu:

Zostrojiť ľavú vetvu hyperboly nebude ťažké, tu len pomôže zvláštnosť funkcie. Zhruba povedané, v bodovej konštrukčnej tabuľke mentálne pridajte ku každému číslu mínus, vložte príslušné bodky a nakreslite druhú vetvu.

Podrobné geometrické informácie o uvažovanej priamke nájdete v článku Hyperbola a parabola.

Graf exponenciálnej funkcie

V tomto odseku sa budem okamžite zaoberať exponenciálnou funkciou, pretože v úlohách vyššej matematiky sa v 95% prípadov vyskytuje práve exponent.

Pripomínam vám, že - toto je iracionálne číslo: bude to potrebné pri zostavovaní grafu, ktorý v skutočnosti postavím bez obradu. Tri body asi stačia:

Graf funkcie nechajme zatiaľ na pokoji, o tom neskôr.

Hlavné vlastnosti funkcie:

V zásade vyzerajú grafy funkcií rovnako atď.

Musím povedať, že druhý prípad je v praxi menej bežný, ale vyskytuje sa, preto som považoval za potrebné zahrnúť ho do tohto článku.

Graf logaritmickej funkcie

Zvážte funkciu s prirodzeným logaritmom.
Urobme si čiarovú kresbu:

Ak ste zabudli, čo je logaritmus, pozrite si prosím školské učebnice.

Hlavné vlastnosti funkcie:

doména:

Rozsah hodnôt: .

Funkcia nie je obmedzená zhora: , aj keď pomaly, ale vetva logaritmu ide až do nekonečna.
Pozrime sa na správanie funkcie blízko nuly vpravo: . Takže os je vertikálna asymptota pre graf funkcie s "x" smerujúcim k nule vpravo.

Nezabudnite poznať a zapamätať si typickú hodnotu logaritmu: .

Graf logaritmu na základe vyzerá v zásade rovnako: , , (desatinný logaritmus na základ 10) atď. Zároveň platí, že čím väčšia základňa, tým plochejší bude graf.

Nebudeme zvažovať prípad, niečo, čo si nepamätám, kedy som naposledy zostavil graf s takýmto základom. Áno, a logaritmus sa zdá byť veľmi zriedkavým hosťom v problémoch vyššej matematiky.

Na záver odseku poviem ešte jednu skutočnosť: Exponenciálna funkcia a logaritmická funkciasú dve vzájomne inverzné funkcie. Ak sa pozriete pozorne na graf logaritmu, môžete vidieť, že ide o rovnaký exponent, len je umiestnený trochu inak.

Grafy goniometrických funkcií

Ako začína trigonometrické trápenie v škole? Správny. Zo sínusu

Nakreslíme funkciu

Táto linka je tzv sínusoida.

Pripomínam vám, že „pí“ je iracionálne číslo: a pri trigonometrii oslňuje oči.

Hlavné vlastnosti funkcie:

Táto funkcia je periodikum s bodkou. Čo to znamená? Pozrime sa na strih. Naľavo a napravo od neho sa donekonečna opakuje presne tá istá časť grafu.

doména: , to znamená, že pre akúkoľvek hodnotu "x" existuje sínusová hodnota.

Rozsah hodnôt: . Funkcia je obmedzené: , to znamená, že všetky „hry“ sedia striktne v segmente .
To sa nestane: alebo presnejšie, stane sa, ale tieto rovnice nemajú riešenie.