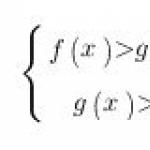Disuguaglianze logaritmiche
Nelle lezioni precedenti, abbiamo familiarizzato con le equazioni logaritmiche e ora sappiamo cosa sono e come risolverle. E la lezione di oggi sarà dedicata allo studio delle disuguaglianze logaritmiche. Quali sono queste disuguaglianze e qual è la differenza tra la risoluzione di un'equazione logaritmica e le disuguaglianze?
Le disuguaglianze logaritmiche sono disuguaglianze che hanno una variabile sotto il segno del logaritmo o alla sua base.
Oppure si può anche dire che una disuguaglianza logaritmica è una tale disuguaglianza in cui il suo valore sconosciuto, come nell'equazione logaritmica, sarà sotto il segno del logaritmo.
Le disuguaglianze logaritmiche più semplici si presentano così:
dove f(x) e g(x) sono alcune espressioni che dipendono da x.
Diamo un'occhiata a questo usando il seguente esempio: f(x)=1+2x+x2, g(x)=3x−1.
Risolvere le disuguaglianze logaritmiche
Prima di risolvere le disuguaglianze logaritmiche, vale la pena notare che quando vengono risolte, sono simili alle disuguaglianze esponenziali, vale a dire:
In primo luogo, quando si passa dai logaritmi alle espressioni sotto il segno del logaritmo, è necessario confrontare anche la base del logaritmo con uno;
In secondo luogo, quando si risolve una disuguaglianza logaritmica utilizzando un cambiamento di variabili, è necessario risolvere le disuguaglianze rispetto al cambiamento fino a ottenere la disuguaglianza più semplice.
Ma siamo stati noi a considerare i momenti simili di risoluzione delle disuguaglianze logaritmiche. Ora diamo un'occhiata a una differenza piuttosto significativa. Tu ed io sappiamo che la funzione logaritmica ha un dominio di definizione limitato, quindi quando si passa dai logaritmi alle espressioni sotto il segno del logaritmo, è necessario tenere conto dell'intervallo di valori accettabili (ODV).
Cioè, va tenuto presente che quando si risolve un'equazione logaritmica, possiamo prima trovare le radici dell'equazione e quindi verificare questa soluzione. Ma risolvere la disuguaglianza logaritmica non funzionerà in questo modo, poiché passando dai logaritmi alle espressioni sotto il segno del logaritmo, sarà necessario annotare la ODZ della disuguaglianza.
Inoltre, vale la pena ricordare che la teoria delle disuguaglianze consiste in numeri reali, che sono numeri positivi e negativi, oltre al numero 0.
Ad esempio, quando il numero "a" è positivo, è necessario utilizzare la seguente notazione: a > 0. In questo caso, anche la somma e il prodotto di tali numeri saranno positivi.
Il principio di base per risolvere una disuguaglianza è sostituirla con una disuguaglianza più semplice, ma la cosa principale è che sia equivalente a quella data. Inoltre, abbiamo anche ottenuto una disuguaglianza e l'abbiamo sostituita di nuovo con una di forma più semplice, e così via.
Risolvendo le disuguaglianze con una variabile, devi trovare tutte le sue soluzioni. Se due disuguaglianze hanno la stessa variabile x, allora tali disuguaglianze sono equivalenti, a condizione che le loro soluzioni siano le stesse.
Quando si eseguono compiti per risolvere le disuguaglianze logaritmiche, è necessario ricordare che quando a > 1, la funzione logaritmica aumenta e quando 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Modi per risolvere le disuguaglianze logaritmiche
Ora diamo un'occhiata ad alcuni dei metodi che hanno luogo quando si risolvono le disuguaglianze logaritmiche. Per una migliore comprensione e assimilazione, cercheremo di capirli utilizzando esempi specifici.
Sappiamo che la più semplice disuguaglianza logaritmica ha la seguente forma:
In questa disuguaglianza, V - è uno di tali segni di disuguaglianza come:<,>, ≤ o ≥.
Quando la base di questo logaritmo è maggiore di uno (a>1), effettuando il passaggio dai logaritmi alle espressioni sotto il segno del logaritmo, in questa versione viene preservato il segno di disuguaglianza e la disuguaglianza sarà simile a questa:
che è equivalente al seguente sistema:

Nel caso in cui la base del logaritmo sia maggiore di zero e minore di uno (0 Questo è equivalente a questo sistema: Diamo un'occhiata ad altri esempi di risoluzione delle disuguaglianze logaritmiche più semplici mostrate nell'immagine seguente: Esercizio. Proviamo a risolvere questa disuguaglianza: La decisione dell'area dei valori ammissibili. Ora proviamo a moltiplicare il suo lato destro per: Vediamo cosa possiamo fare: Passiamo ora alla trasformazione delle espressioni sublogaritmiche. Poiché la base del logaritmo è 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: 3x - 8 > 16; E da ciò ne consegue che l'intervallo che abbiamo ottenuto appartiene interamente alla ODZ ed è una soluzione a tale disuguaglianza. Ecco la risposta che abbiamo ottenuto: Proviamo ora ad analizzare ciò di cui abbiamo bisogno per risolvere con successo le disuguaglianze logaritmiche? In primo luogo, concentra tutta la tua attenzione e cerca di non commettere errori quando esegui le trasformazioni date in questa disuguaglianza. Inoltre, va ricordato che quando si risolvono tali disuguaglianze, è necessario prevenire espansioni e restringimenti della disuguaglianza ODZ, che possono portare alla perdita o all'acquisizione di soluzioni estranee. In secondo luogo, quando si risolvono le disuguaglianze logaritmiche, è necessario imparare a pensare in modo logico e comprendere la differenza tra concetti come un sistema di disuguaglianze e un insieme di disuguaglianze, in modo da poter selezionare facilmente soluzioni a una disuguaglianza, pur essendo guidato dal suo DHS. In terzo luogo, per risolvere con successo tali disuguaglianze, ognuno di voi deve conoscere perfettamente tutte le proprietà delle funzioni elementari e comprenderne chiaramente il significato. Tali funzioni includono non solo logaritmiche, ma anche razionali, di potenza, trigonometriche, ecc., in una parola, tutte quelle che hai studiato durante l'algebra scolastica. Come puoi vedere, dopo aver studiato il tema delle disuguaglianze logaritmiche, non c'è nulla di difficile nel risolvere queste disuguaglianze, a condizione che tu sia attento e persistente nel raggiungere i tuoi obiettivi. Per evitare problemi nella risoluzione delle disuguaglianze, è necessario allenarsi il più possibile, risolvendo vari compiti e allo stesso tempo memorizzare i modi principali per risolvere tali disuguaglianze e i loro sistemi. Con soluzioni infruttuose alle disuguaglianze logaritmiche, dovresti analizzare attentamente i tuoi errori in modo da non tornarci più in futuro. Per una migliore assimilazione dell'argomento e consolidamento del materiale trattato, risolvi le seguenti disuguaglianze: Con loro sono all'interno dei logaritmi. Esempi: \(\log_3x≥\log_39\) Qualsiasi disuguaglianza logaritmica dovrebbe essere ridotta alla forma \(\log_a(f(x)) ˅ \log_a(g(x))\) (il simbolo \(˅\) indica uno qualsiasi di ). Questa forma ci permette di sbarazzarci dei logaritmi e delle loro basi passando alla disuguaglianza delle espressioni sotto logaritmi, cioè alla forma \(f(x) ˅ g(x)\). Ma quando si effettua questa transizione, c'è una sottigliezza molto importante: \(\log_2((8-x))<1\) Soluzione: \(\log\)\(_(0.5)\) \((2x-4)\)≥\(\log\)\(_(0.5)\) \(((x+ uno))\) Soluzione: Molto importante! In qualsiasi disuguaglianza, la transizione dalla forma \(\log_a(f(x)) ˅ \log_a(g(x))\) al confronto di espressioni sotto logaritmi può essere eseguita solo se: Esempio
. Risolvi la disuguaglianza: \(\log\)\(≤-1\) Soluzione:
\(\tronco d'albero\) \(_(\frac(1)(3))(\frac(3x-2)(2x-3))\)\(≤-1\) Scriviamo l'ODZ. ODZ: \(\frac(3x-2)(2x-3)\) \(>0\) \(\frac(3x-2-3(2x-3))(2x-3)\)\(≥\) \(0\) Apriamo le parentesi, diamo . \(\frac(-3x+7)(2x-3)\) \(≥\) \(0\) Moltiplichiamo la disuguaglianza per \(-1\), ricordandoci di invertire il segno di confronto. \(\frac(3x-7)(2x-3)\) \(≤\) \(0\) \(\frac(3(x-\frac(7)(3)))(2(x-\frac(3)(2)))\)\(≤\) \(0\) Costruiamo una linea numerica e segniamo i punti \(\frac(7)(3)\) e \(\frac(3)(2)\) su di essa. Si noti che il punto dal denominatore è forato, nonostante il fatto che la disuguaglianza non sia rigorosa. Il fatto è che questo punto non sarà una soluzione, poiché quando si sostituisce una disuguaglianza, ci porterà alla divisione per zero. Ora tracciamo la ODZ sullo stesso asse numerico e scriviamo in risposta l'intervallo che cade nella ODZ. Scrivi la risposta finale. Esempio
. Risolvi la disuguaglianza: \(\log^2_3x-\log_3x-2>0\) Soluzione:
\(\log^2_3x-\log_3x-2>0\) Scriviamo l'ODZ. ODZ: \(x>0\) Veniamo alla soluzione. Soluzione: \(\log^2_3x-\log_3x-2>0\) Davanti a noi c'è una tipica disuguaglianza logaritmica quadrata. Noi facciamo. \(t=\log_3x\) \(D=1+8=9\) Ora devi tornare alla variabile originale - x. Per fare ciò, passiamo a , che ha la stessa soluzione, e facciamo la sostituzione inversa. \(\left[ \begin(raccolti) t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2 \\ \log_3x<-1 \end{gathered} \right.\) Trasforma \(2=\log_39\), \(-1=\log_3\frac(1)(3)\). \(\left[ \begin(raccolti) \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) Passiamo al confronto delle argomentazioni. Le basi dei logaritmi sono maggiori di \(1\), quindi il segno delle disuguaglianze non cambia. \(\left[ \begin(raccolti) x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) Uniamo la soluzione della disuguaglianza e l'ODZ in una figura. Scriviamo la risposta. Tra l'intera varietà di disuguaglianze logaritmiche, le disuguaglianze a base variabile sono studiate separatamente. Sono risolti secondo una formula speciale, che per qualche motivo viene insegnata raramente a scuola: log k (x ) f (x ) ∨ log k (x ) g (x ) ⇒ (f (x ) − g (x )) (k (x ) − 1) ∨ 0 Invece di una taccola "∨", puoi mettere qualsiasi segno di disuguaglianza: più o meno. La cosa principale è che in entrambe le disuguaglianze i segni sono gli stessi. Quindi eliminiamo i logaritmi e riduciamo il problema a una disuguaglianza razionale. Quest'ultimo è molto più facile da risolvere, ma quando si scartano i logaritmi possono apparire radici extra. Per tagliarli è sufficiente trovare l'intervallo di valori ammissibili. Se hai dimenticato l'ODZ del logaritmo, ti consiglio vivamente di ripeterlo - vedi "Cos'è un logaritmo". Tutto ciò che riguarda l'intervallo di valori accettabili deve essere scritto e risolto separatamente: f(x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1. Queste quattro disuguaglianze costituiscono un sistema e devono essere soddisfatte simultaneamente. Quando viene trovata la gamma di valori accettabili, resta da incrociarla con la soluzione di una disuguaglianza razionale - e la risposta è pronta. Compito. Risolvi la disuguaglianza: Per prima cosa, scriviamo la ODZ del logaritmo: Le prime due disuguaglianze vengono eseguite automaticamente e l'ultima dovrà essere scritta. Poiché il quadrato di un numero è zero se e solo se il numero stesso è zero, abbiamo: x 2 + 1 ≠ 1; Risulta che la ODZ del logaritmo è tutti i numeri tranne zero: x ∈ (−∞ 0)∪(0; +∞). Ora risolviamo la disuguaglianza principale: Eseguiamo il passaggio dalla disuguaglianza logaritmica a quella razionale. Nella disuguaglianza originale c'è un segno "minore di", quindi anche la disuguaglianza risultante dovrebbe essere con un segno "minore di". Abbiamo: (10 - (x 2 + 1)) (x 2 + 1 - 1)< 0; Zeri di questa espressione: x = 3; x = -3; x = 0. Inoltre, x = 0 è la radice della seconda molteplicità, il che significa che passando per essa il segno della funzione non cambia. Abbiamo: Otteniamo x ∈ (−∞ −3)∪(3; +∞). Questo insieme è completamente contenuto nell'ODZ del logaritmo, il che significa che questa è la risposta. Spesso la disuguaglianza originale differisce da quella sopra. Questo è facile da risolvere secondo le regole standard per lavorare con i logaritmi - vedere "Proprietà di base dei logaritmi". Vale a dire: Separatamente, voglio ricordarti l'intervallo di valori accettabili. Poiché possono esserci diversi logaritmi nella disuguaglianza originale, è necessario trovare il DPV di ciascuno di essi. Pertanto, lo schema generale per risolvere le disuguaglianze logaritmiche è il seguente: Compito. Risolvi la disuguaglianza: Trova il dominio di definizione (ODZ) del primo logaritmo: Risolviamo con il metodo dell'intervallo. Trovare gli zeri del numeratore: 3x - 2 = 0; Quindi - gli zeri del denominatore: x - 1 = 0; Segniamo zeri e segni sulla freccia delle coordinate: Otteniamo x ∈ (−∞ 2/3)∪(1; +∞). Il secondo logaritmo dell'ODZ sarà lo stesso. Se non mi credi, puoi controllare. Ora trasformiamo il secondo logaritmo in modo che la base sia due: Come puoi vedere, le triple alla base e prima del logaritmo si sono ridotte. Ottieni due logaritmi con la stessa base. Mettiamoli insieme: log 2 (x - 1) 2< 2; Abbiamo ottenuto la disuguaglianza logaritmica standard. Eliminiamo i logaritmi con la formula. Poiché nella disuguaglianza originale è presente un segno minore di, anche l'espressione razionale risultante deve essere minore di zero. Abbiamo: (f (x) - g (x)) (k (x) - 1)< 0; Abbiamo due set: Resta da attraversare questi insiemi: otteniamo la vera risposta: Siamo interessati all'intersezione degli insiemi, quindi scegliamo gli intervalli ombreggiati su entrambe le frecce. Otteniamo x ∈ (−1; 2/3)∪(1; 3) - tutti i punti sono punteggiati. DISUGUAGLIANZE LOGARITMICHE NELL'USO
Sechin Mikhail Aleksandrovic Piccola Accademia delle Scienze per Studenti della Repubblica del Kazakistan "Seeker" MBOU "Scuola secondaria sovietica n. 1", grado 11, città. Distretto Sovietico Sovietsky Gunko Lyudmila Dmitrievna, insegnante di MBOU "Scuola secondaria sovietica n. 1" distretto di Sovietsky Obbiettivo: studio del meccanismo per risolvere le disuguaglianze logaritmiche C3 utilizzando metodi non standard, rivelando fatti interessanti sul logaritmo. Materia di studio:
3) Imparare a risolvere specifiche disuguaglianze logaritmiche C3 usando metodi non standard. Risultati:
Contenuto
Introduzione…………………………………………………………………………………….4
Capitolo 1. Contesto……………………………………………………………...5
Capitolo 2. Raccolta delle disuguaglianze logaritmiche …………………………… 7
2.1. Transizioni equivalenti e metodo generalizzato degli intervalli…………… 7 2.2. Metodo di razionalizzazione ……………………………………………………… 15 2.3. Sostituzione non standard…………………………………………………………………………………………………………………………………………………………………………………………………. 2.4. Compiti con trappole………………………………………………………… 27 Conclusione………………………………………………………………………… 30
Letteratura……………………………………………………………………. 31
introduzione
Sono all'undicesimo anno e ho intenzione di entrare in un'università in cui la matematica è una materia fondamentale. Ed è per questo che lavoro molto con i compiti della parte C. Nel compito C3, devi risolvere una disuguaglianza non standard o un sistema di disuguaglianze, solitamente associato ai logaritmi. Mentre mi preparavo all'esame, ho riscontrato il problema della mancanza di metodi e tecniche per risolvere le disuguaglianze logaritmiche d'esame offerte in C3. I metodi che vengono studiati nel curriculum scolastico su questo argomento non forniscono una base per risolvere i compiti C3. L'insegnante di matematica mi ha suggerito di lavorare con i compiti C3 da solo sotto la sua guida. Inoltre, mi interessava la domanda: ci sono logaritmi nella nostra vita? In quest'ottica è stato scelto il tema: "Disequazioni logaritmiche nell'esame"
Obbiettivo: studio del meccanismo per risolvere problemi C3 utilizzando metodi non standard, rivelando fatti interessanti sul logaritmo. Materia di studio:
1) Trova le informazioni necessarie sui metodi non standard per risolvere le disuguaglianze logaritmiche. 2) Trova ulteriori informazioni sui logaritmi. 3) Impara a risolvere specifici problemi C3 usando metodi non standard. Risultati:
Il significato pratico risiede nell'ampliamento dell'apparato per la risoluzione dei problemi C3. Questo materiale può essere utilizzato in alcune lezioni, per circoli direttivi, lezioni facoltative di matematica. Il prodotto del progetto sarà la raccolta "Disuguaglianze logaritmiche C3 con soluzioni". Capitolo 1. Sfondo
Durante il XVI secolo, il numero di calcoli approssimativi aumentò rapidamente, principalmente in astronomia. Il miglioramento degli strumenti, lo studio dei movimenti planetari e altri lavori richiedevano calcoli colossali, a volte molti anni. L'astronomia correva il rischio reale di annegare in calcoli non realizzati. Difficoltà sono emerse anche in altri ambiti, ad esempio nel settore assicurativo sono state necessarie tabelle di interessi composti per vari valori percentuali. La difficoltà principale era la moltiplicazione, la divisione di numeri a più cifre, in particolare le quantità trigonometriche. La scoperta dei logaritmi si basava sulle note proprietà delle progressioni alla fine del XVI secolo. Archimede ha parlato della connessione tra i membri della progressione geometrica q, q2, q3, ... e la progressione aritmetica dei loro indicatori 1, 2, 3, ... nel Salmite. Un altro prerequisito era l'estensione del concetto di grado agli esponenti negativi e frazionari. Molti autori hanno sottolineato che moltiplicazione, divisione, elevazione a potenza ed estrazione di una radice corrispondono in modo esponenziale in aritmetica - nello stesso ordine - addizione, sottrazione, moltiplicazione e divisione. Ecco l'idea del logaritmo come esponente. Nella storia dello sviluppo della dottrina dei logaritmi sono trascorse diverse fasi. Fase 1
I logaritmi furono inventati non più tardi del 1594 indipendentemente dal barone scozzese Napier (1550-1617) e dieci anni dopo dal meccanico svizzero Burgi (1552-1632). Entrambi volevano fornire un nuovo mezzo conveniente per i calcoli aritmetici, sebbene affrontassero questo problema in modi diversi. Napier espresse cinematicamente la funzione logaritmica ed entrò così in un nuovo campo della teoria delle funzioni. Bürgi rimase sulla base della considerazione di progressioni discrete. Tuttavia, la definizione del logaritmo per entrambi non è simile a quella moderna. Il termine "logaritmo" (logaritmo) appartiene a Napier. Nasce da una combinazione di parole greche: logos - "relazione" e ariqmo - "numero", che significava "numero di relazioni". Inizialmente, Napier usò un termine diverso: numeri artificiales - "numeri artificiali", in contrapposizione a numeri naturalts - "numeri naturali". Nel 1615, in una conversazione con Henry Briggs (1561-1631), professore di matematica al Gresh College di Londra, Napier suggerì di prendere zero per il logaritmo di uno e 100 per il logaritmo di dieci, o ciò che equivale a , solo 1. Ecco come sono stati stampati i logaritmi decimali e le prime tabelle logaritmiche. Successivamente, le tavole Briggs furono integrate dal libraio e matematico olandese Andrian Flakk (1600-1667). Napier e Briggs, sebbene arrivassero ai logaritmi prima di chiunque altro, pubblicarono le loro tabelle più tardi di altre - nel 1620. Il registro dei segni e il registro furono introdotti nel 1624 da I. Keplero. Il termine "logaritmo naturale" fu introdotto da Mengoli nel 1659, seguito da N. Mercator nel 1668, e l'insegnante londinese John Spadel pubblicò tabelle di logaritmi naturali di numeri da 1 a 1000 sotto il nome di "Nuovi logaritmi". In russo, le prime tavole logaritmiche furono pubblicate nel 1703. Ma in tutte le tabelle logaritmiche sono stati commessi errori nel calcolo. Le prime tabelle prive di errori furono pubblicate nel 1857 a Berlino nell'elaborazione del matematico tedesco K. Bremiker (1804-1877). Fase 2
L'ulteriore sviluppo della teoria dei logaritmi è associato a una più ampia applicazione della geometria analitica e del calcolo infinitesimale. A quel punto è stata stabilita la connessione tra la quadratura di un'iperbole equilatera e il logaritmo naturale. La teoria dei logaritmi di questo periodo è associata ai nomi di numerosi matematici. Il matematico, astronomo e ingegnere tedesco Nikolaus Mercator nel suo saggio "Logarithmotechnics" (1668) fornisce una serie che dà l'espansione di ln(x + 1) in termini di potenze x: Questa espressione corrisponde esattamente al corso del suo pensiero, sebbene, ovviamente, non usasse i segni d, ..., ma simboli più ingombranti. Con la scoperta delle serie logaritmiche, la tecnica per il calcolo dei logaritmi cambiò: iniziarono a essere determinati utilizzando le serie infinite. Nelle sue lezioni "La matematica elementare da un punto di vista superiore", lette nel 1907-1908, F. Klein suggerì di utilizzare la formula come punto di partenza per costruire la teoria dei logaritmi. Fase 3
Definizione di funzione logaritmica in funzione dell'inversa esponenziale, logaritmo come esponente di una data base non è stato formulato immediatamente. L'opera di Leonhard Euler (1707-1783) "Introduzione all'analisi degli infinitesimi" (1748) è servito come ulteriore sviluppo della teoria della funzione logaritmica. In questo modo, Sono passati 134 anni dalla prima introduzione dei logaritmi (contando dal 1614) prima che i matematici trovassero una definizione il concetto di logaritmo, che oggi è alla base del percorso scolastico. Capitolo 2. Raccolta delle disuguaglianze logaritmiche
2.1. Transizioni equivalenti e metodo generalizzato degli intervalli. Transizioni equivalenti
Metodo dell'intervallo generalizzato
Questo metodo è il più universale per risolvere disuguaglianze di quasi ogni tipo. Lo schema della soluzione si presenta così: 1. Porta la disuguaglianza in un tale modulo, dove la funzione si trova sul lato sinistro 2. Trova l'ambito della funzione 3. Trova gli zeri di una funzione 4. Disegna il dominio di definizione e gli zeri della funzione su una retta reale. 5. Determinare i segni della funzione 6. Selezionare gli intervalli in cui la funzione assume i valori necessari e annotare la risposta. Esempio 1
Soluzione:
Applicare il metodo dell'intervallo dove Per questi valori, tutte le espressioni sotto i segni dei logaritmi sono positive. Risposta:
Esempio 2
Soluzione:
1°
modo
.
ODZ è determinato dalla disuguaglianza X> 3. Prendere i logaritmi per tali X in base 10, otteniamo L'ultima disuguaglianza potrebbe essere risolta applicando le regole di scomposizione, cioè confrontando i fattori con zero. Tuttavia, in questo caso è facile determinare gli intervalli di costanza della funzione quindi è possibile applicare il metodo dell'intervallo. Funzione F(X) = 2X(X- 3.5)lgǀ X- 3ǀ è continuo per X> 3 e scompare nei punti X 1 = 0, X 2 = 3,5, X 3 = 2, X 4 = 4. Quindi, determiniamo gli intervalli di costanza della funzione F(X):
Risposta: 2a via
.
Applichiamo le idee del metodo degli intervalli direttamente alla disuguaglianza originaria. Per questo, ricordiamo che le espressioni un B- un c e ( un - 1)(B- 1) avere un segno. Poi la nostra disuguaglianza per X> 3 è equivalente alla disuguaglianza o L'ultima disuguaglianza viene risolta con il metodo dell'intervallo Risposta: Esempio 3
Soluzione:
Applicare il metodo dell'intervallo Risposta: Esempio 4
Soluzione:
Dal 2 X 2 - 3X+ 3 > 0 per tutti i reali X, poi Per risolvere la seconda disuguaglianza, utilizziamo il metodo dell'intervallo Nella prima disuguaglianza, facciamo il cambiamento quindi arriviamo alla disuguaglianza 2y 2 - y - 1 < 0 и, применив метод интервалов, получаем, что решениями будут те y, che soddisfano la disuguaglianza -0,5< y < 1.
Da dove, perché otteniamo la disuguaglianza che si effettua con X, per cui 2 X 2 - 3X - 5 < 0. Вновь применим метод интервалов
Ora, tenendo conto della soluzione della seconda disuguaglianza del sistema, otteniamo finalmente Risposta:
Esempio 5
Soluzione:
La disuguaglianza è equivalente a un insieme di sistemi o Applicare il metodo dell'intervallo o Risposta:
Esempio 6
Soluzione:
La disuguaglianza equivale a un sistema Permettere poi y > 0,
e la prima disuguaglianza il sistema prende la forma o, in espansione trinomio quadrato a fattori, Applicando il metodo dell'intervallo all'ultima disuguaglianza, vediamo che le sue soluzioni soddisfano la condizione y> 0 sarà tutto y > 4.
Pertanto, la disuguaglianza originale è equivalente al sistema: Quindi, le soluzioni della disuguaglianza sono tutte 2.2. metodo di razionalizzazione. In precedenza, il metodo di razionalizzazione della disuguaglianza non era risolto, non era noto. Questo è "un nuovo metodo moderno ed efficace per risolvere le disuguaglianze esponenziali e logaritmiche" (citazione dal libro di Kolesnikova S.I.) "Tavola magica"
In altre fonti
Se a >1 e b >1, quindi log a b >0 e (a -1)(b -1)>0; Se a >1 e 0 se 0<un<1 и b
>1, quindi registrare a b<0 и (a
-1)(b
-1)<0;
se 0<un<1 и 00 e (a -1)(b -1)>0. Il ragionamento di cui sopra è semplice, ma semplifica notevolmente la soluzione delle disuguaglianze logaritmiche. Esempio 4
log x (x 2 -3)<0
Soluzione:
Esempio 5
log 2 x (2x 2 -4x +6)≤log 2 x (x 2 +x ) Soluzione: Esempio 6
Per risolvere questa disuguaglianza, scriviamo (x-1-1) (x-1) invece del denominatore e il prodotto (x-1) (x-3-9 + x) invece del numeratore. Esempio 7
Esempio 8
2.3. Sostituzione non standard. Esempio 1
Esempio 2
Esempio 3
Esempio 4
Esempio 5
Esempio 6
Esempio 7
log 4 (3 x -1) log 0,25 Facciamo la sostituzione y=3 x -1; allora questa disuguaglianza prende forma registro 4 registro 0,25 Perché registro 0,25 Facciamo una sostituzione t =log 4 y e otteniamo la disuguaglianza t 2 -2t +≥0, la cui soluzione sono gli intervalli - Quindi, per trovare i valori di y, abbiamo un insieme di due disuguaglianze più semplici Pertanto, la disuguaglianza originale è equivalente all'insieme di due disuguaglianze esponenziali, La soluzione della prima disuguaglianza di questo insieme è l'intervallo 0<х≤1, решением второго – промежуток 2≤х<+ Esempio 8
Soluzione:
La disuguaglianza equivale a un sistema La soluzione della seconda disuguaglianza, che determina l'ODZ, sarà l'insieme di quelle X,
per cui X > 0.
Per risolvere la prima disuguaglianza, apportiamo la modifica Quindi otteniamo la disuguaglianza o L'insieme delle soluzioni dell'ultima disuguaglianza si trova con il metodo intervalli: -1< T < 2. Откуда, возвращаясь к переменной X, noi abbiamo o Molti di quelli X, che soddisfano l'ultima disuguaglianza appartiene a ODZ ( X> 0), quindi, è una soluzione del sistema, e quindi la disuguaglianza originaria. Risposta: 2.4. Compiti con trappole. Esempio 1
Soluzione. La ODZ della disuguaglianza è tutta x che soddisfa la condizione 0 Esempio 2
log 2 (2x +1-x 2)>log 2 (2x-1 +1-x)+1. Conclusione
Non è stato facile trovare metodi speciali per risolvere i problemi C3 da una grande varietà di diverse fonti educative. Nel corso del lavoro svolto, ho potuto studiare metodi non standard per la risoluzione di disuguaglianze logaritmiche complesse. Questi sono: le transizioni equivalenti e il metodo generalizzato degli intervalli, il metodo di razionalizzazione ,
sostituzione non standard ,
compiti con trappole sull'ODZ. Questi metodi sono assenti nel curriculum scolastico. Utilizzando metodi diversi, ho risolto 27 disuguaglianze offerte all'USE nella parte C, ovvero C3. Queste disuguaglianze con soluzioni per metodi hanno costituito la base della raccolta "Disuguaglianze logaritmiche C3 con soluzioni", che è diventata il prodotto del progetto della mia attività. L'ipotesi che avevo avanzato all'inizio del progetto è stata confermata: i problemi C3 possono essere risolti efficacemente se si conoscono questi metodi. Inoltre, ho scoperto fatti interessanti sui logaritmi. È stato interessante per me farlo. I prodotti del mio progetto saranno utili sia per gli studenti che per gli insegnanti. Conclusioni:
Pertanto, l'obiettivo del progetto è raggiunto, il problema è risolto. E ho avuto l'esperienza più completa e versatile nelle attività di progetto in tutte le fasi del lavoro. Nel corso del lavoro sul progetto, il mio principale impatto sullo sviluppo è stato sulla competenza mentale, le attività legate alle operazioni mentali logiche, lo sviluppo della competenza creativa, l'iniziativa personale, la responsabilità, la perseveranza e l'attività. Una garanzia di successo nella creazione di un progetto di ricerca per Sono diventato: esperienza scolastica significativa, capacità di estrarre informazioni da varie fonti, verificarne l'affidabilità, classificarla in base al suo significato. Oltre alla conoscenza diretta della matematica, ha ampliato le sue abilità pratiche nel campo dell'informatica, ha acquisito nuove conoscenze ed esperienze nel campo della psicologia, ha stabilito contatti con i compagni di classe e ha imparato a collaborare con gli adulti. Nel corso delle attività progettuali sono state sviluppate capacità e capacità educative generali organizzative, intellettuali e comunicative. Letteratura
1. Koryanov A. G., Prokofiev A. A. Sistemi di disuguaglianze con una variabile (compiti tipici C3). 2. Malkova A. G. Preparazione per l'esame di stato unificato in matematica. 3. S. S. Samarova, Soluzione delle disuguaglianze logaritmiche. 4. Matematica. Raccolta di lavori di formazione a cura di A.L. Semyonov e I.V. Yashchenko. -M.: MTsNMO, 2009. - 72 p.-
Obiettivi della lezione: Didattico: Sviluppando: sviluppare memoria, attenzione, pensiero logico, capacità di confronto, essere in grado di generalizzare e trarre conclusioni Educativo: coltivare la precisione, la responsabilità per il compito svolto, l'assistenza reciproca. Metodi di insegnamento:
verbale ,
visivo ,
pratico ,
ricerca parziale ,
autogoverno ,
controllo. Forme di organizzazione dell'attività cognitiva degli studenti:
frontale ,
individuale ,
lavoro in coppia. Attrezzatura:
una serie di attività di test, una nota di riferimento, fogli bianchi per le soluzioni. Tipo di lezione: imparare nuovo materiale. Durante le lezioni 1. Momento organizzativo. Vengono annunciati il tema e gli obiettivi della lezione, lo schema della lezione: ad ogni studente viene consegnata una scheda di valutazione, che lo studente compila durante la lezione; per ogni coppia di studenti - materiali stampati con compiti, è necessario completare i compiti in coppia; fogli bianchi per le decisioni; fogli di riferimento: definizione del logaritmo; grafico di una funzione logaritmica, sue proprietà; proprietà dei logaritmi; algoritmo per la risoluzione delle disuguaglianze logaritmiche. Tutte le decisioni dopo l'autovalutazione sono sottoposte all'insegnante. Foglio di valutazione degli studenti 2. Attualizzazione della conoscenza. Istruzioni per l'insegnante. Ricorda la definizione del logaritmo, il grafico della funzione logaritmica e le sue proprietà. Per fare ciò, leggi il testo alle pp. 88–90, 98–101 del libro di testo "Algebra e l'inizio dell'analisi 10–11" a cura di Sh.A Alimov, Yu.M Kolyagin e altri. Agli studenti vengono consegnate delle schede su cui sono scritti: la definizione del logaritmo; mostra un grafico di una funzione logaritmica, le sue proprietà; proprietà dei logaritmi; algoritmo per la risoluzione di disuguaglianze logaritmiche, un esempio di risoluzione di una disuguaglianza logaritmica che si riduce a uno quadrato. 3. Imparare nuovo materiale. La soluzione delle disuguaglianze logaritmiche si basa sulla monotonia della funzione logaritmica. Algoritmo per la risoluzione delle disuguaglianze logaritmiche: A) Trovare il dominio di definizione della disuguaglianza (l'espressione sublogaritmica è maggiore di zero). Elemento di apprendimento n. 1. Scopo: correggere la soluzione delle più semplici disuguaglianze logaritmiche Forma di organizzazione dell'attività cognitiva degli studenti: lavoro individuale. Compiti per lavoro indipendente per 10 minuti. Per ogni disuguaglianza ci sono diverse risposte, devi scegliere quella giusta e controllare per chiave. Elemento di apprendimento n. 2. Scopo: correggere la soluzione delle disuguaglianze logaritmiche applicando le proprietà dei logaritmi. Istruzioni per l'insegnante. Richiama le proprietà di base dei logaritmi. Per fare ciò, leggi il testo del libro di testo a p.92, 103–104. Compiti per lavoro indipendente per 10 minuti. LEGENDA: 2113, il numero massimo di punti è 8 b. Elemento di apprendimento n. 3. Scopo: studiare la soluzione delle disuguaglianze logaritmiche mediante il metodo della riduzione al quadrato. Istruzioni per l'insegnante: il metodo per ridurre la disuguaglianza a un quadrato è che devi trasformare la disuguaglianza in una forma tale che una certa funzione logaritmica sia indicata da una nuova variabile, ottenendo una disuguaglianza quadrata rispetto a questa variabile. Usiamo il metodo dell'intervallo. Hai superato il primo livello di assimilazione del materiale. Ora dovrai scegliere autonomamente un metodo per risolvere le equazioni logaritmiche, usando tutte le tue conoscenze e capacità. Elemento di apprendimento numero 4. Scopo: consolidare la soluzione delle disuguaglianze logaritmiche scegliendo un modo razionale per risolverlo da soli. Compiti per lavoro indipendente per 10 minuti Elemento di apprendimento numero 5. Istruzioni per l'insegnante. Molto bene! Hai imparato la soluzione di equazioni del secondo livello di complessità. Lo scopo del tuo ulteriore lavoro è applicare le tue conoscenze e abilità in situazioni più complesse e non standard. Compiti per una soluzione indipendente: Istruzioni per l'insegnante. È fantastico se hai fatto tutto il lavoro. Molto bene! Il voto per l'intera lezione dipende dal numero di punti ottenuti per tutti gli elementi educativi: Volpi stimate da consegnare all'insegnante. 5. Compiti a casa: se hai ottenuto un punteggio non superiore a 15 b - lavora sugli errori (le soluzioni possono essere prese dall'insegnante), se hai ottenuto un punteggio superiore a 15 b - esegui un compito creativo sull'argomento "Disuguaglianze logaritmiche".

Soluzione di esempi
![]()



3x > 24;
x > 8. ![]()
Cosa è necessario per risolvere le disuguaglianze logaritmiche?
Compiti a casa

\(\log_3 ((x^2-3))< \log_3{(2x)}\)
\(\log_(x+1)((x^2+3x-7))>2\)
\(\lg^2((x+1))+10≤11 \lg((x+1))\)Come risolvere le disuguaglianze logaritmiche:
\(-\) se - un numero ed è maggiore di 1 - il segno di disuguaglianza rimane lo stesso durante la transizione,
\(-\) se la base è un numero maggiore di 0 ma minore di 1 (tra zero e uno), allora il segno di disuguaglianza deve essere invertito, cioè
ODZ: \(8-x>0\)
\(-x>-8\)
\(X<8\)
\(\log\)\(_2\) \((8-x)<\log\)\(_2\)
\({2}\)
\(8-x\)\(<\)
\(2\)
\(8-2
Risposta: \((6;8)\)
ODZ: \(\begin(cases)2x-4>0\\x+1 > 0\end(cases)\)
\(\begin(cases)2x>4\\x > -1\end(cases)\) \(\Leftrightarrow\) \(\begin(cases)x>2\\x > -1\end(cases) \) \(\freccia sinistra-destra\) \(x\in(2;\infty)\)
\(2x-4\)\(≤\)\(x+1\)
\(2x-x≤4+1\)
\(x≤5\)
Risposta: \((2;5]\)
Risposta:
\(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)

\(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)

Risposta:
\(((0; \frac(1)(3))∪(9;∞)\)
\(t^2-t-2>0\) Espandi il lato sinistro della disuguaglianza in .
\(t_1= \frac(1+3)(2)=2\)
\(t_2=\frac(1-3)(2)=-1\)
\((t+1)(t-2)>0\)

x2 ≠ 0;
x ≠ 0.
(9 - x2) x2< 0;
(3 - x) (3 + x) x 2< 0.
Trasformazione delle disuguaglianze logaritmiche
x = 2/3.
x = 1.

log 2 (x - 1) 2< log 2 2 2 .
((x - 1) 2 - 2 2)(2 - 1)< 0;
x 2 - 2 x + 1 - 4< 0;
x 2 - 2 x - 3< 0;
(x - 3)(x + 1)< 0;
x ∈ (−1; 3).
 se a > 1
se a > 1 se 0 <
а <
1
se 0 <
а <
1

 e 0 a destra.
e 0 a destra. .
.
 , cioè risolvi l'equazione
, cioè risolvi l'equazione  (e risolvere un'equazione è solitamente più facile che risolvere una disuguaglianza).
(e risolvere un'equazione è solitamente più facile che risolvere una disuguaglianza). agli intervalli ricevuti.
agli intervalli ricevuti.


![]()

![]()
![]()











![]()



![]()





![]()

![]()
![]()
![]()


![]()
E anche se l'insegnante lo conosceva, c'era una paura - ma l'esperto USE lo conosce e perché non lo danno a scuola? Ci sono state situazioni in cui l'insegnante ha detto allo studente: "Dove l'hai preso? Siediti - 2".
Ora il metodo viene promosso ovunque. E per gli esperti, ci sono linee guida associate a questo metodo e in "Le edizioni più complete delle opzioni standard ..." nella soluzione C3 viene utilizzato questo metodo.
IL METODO E' FANTASTICO!






 Risposta. (0; 0,5) U .
Risposta. (0; 0,5) U .


 Risposta :
(3;6)
Risposta :
(3;6)









 .
.
 = -log 4
= -log 4  = -(log 4 y -log 4 16)=2-log 4 y , quindi riscriviamo l'ultima disuguaglianza come 2log 4 y -log 4 2 y ≤.
= -(log 4 y -log 4 16)=2-log 4 y , quindi riscriviamo l'ultima disuguaglianza come 2log 4 y -log 4 2 y ≤.
 La soluzione di questa raccolta sono gli intervalli 0<у≤2 и 8≤у<+
La soluzione di questa raccolta sono gli intervalli 0<у≤2 и 8≤у<+ .
.
 cioè aggregati
cioè aggregati 
 . Pertanto, la disuguaglianza originale vale per tutti i valori di x dagli intervalli 0<х≤1 и 2≤х<+
. Pertanto, la disuguaglianza originale vale per tutti i valori di x dagli intervalli 0<х≤1 и 2≤х<+ .
.


![]()
![]()
![]()


 .
.
 . Pertanto, tutto x dall'intervallo 0
. Pertanto, tutto x dall'intervallo 0
B) Presentare (se possibile) le parti sinistra e destra della disuguaglianza come logaritmi nella stessa base.
C) Determinare se la funzione logaritmica è crescente o decrescente: se t>1, allora crescente; se 0
D) Passare ad una disuguaglianza più semplice (espressioni sublogaritmiche), considerando che il segno di disuguaglianza sarà preservato se la funzione è crescente, e cambierà se è decrescente.
CHIAVE: 13321, punteggio massimo - 6 p.