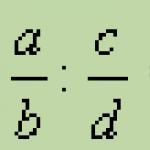Espressioni, conversione di espressioni

Espressioni di potenza (espressioni con potenze) e loro conversione

In questo articolo parleremo della conversione delle espressioni di potenza. Innanzitutto, ci concentreremo sulle trasformazioni eseguite con espressioni di qualsiasi tipo, comprese le espressioni esponenziali, come l'espansione delle parentesi, il lancio di termini simili. E poi analizzeremo le trasformazioni inerenti proprio alle espressioni con potenze: lavorare con la base e l'esponente, usare le proprietà dei gradi, ecc.

Navigazione della pagina.

Cosa sono le espressioni esponenziali?

Il termine "espressioni esponenziali" non si trova praticamente nei libri di testo scolastici di matematica, ma appare abbastanza spesso nelle raccolte di problemi, specialmente quelli progettati per preparare l'esame e OGE, per esempio. Dopo aver analizzato le attività in cui è necessario eseguire azioni con espressioni esponenziali, diventa chiaro che le espressioni sono intese come espressioni che contengono gradi nei loro record. Pertanto, per te stesso, puoi accettare la seguente definizione:

Definizione.

Espressioni di potere Sono espressioni contenenti gradi.

diamo esempi di espressioni esponenziali... Inoltre, li rappresenteremo in base a come avviene lo sviluppo delle opinioni su da un grado con un indicatore naturale a un grado con un indicatore reale.

Come sai, prima c'è una conoscenza della potenza di un numero con un esponente naturale, in questa fase le prime espressioni di potenza più semplici del tipo 3 2, 7 5 +1, (2 + 1) 5, (−0, 1) 4, 3 a 2 −a + a 2, x 3−1, (a 2) 3, ecc.

Poco dopo, viene studiata la potenza di un numero con un esponente intero, che porta alla comparsa di espressioni di potenza con potenze intere negative, come le seguenti: 3 -2, , a -2 + 2 b -3 + c 2.

Al liceo, tornano di nuovo ai gradi. Lì viene introdotto un grado con un esponente razionale, che comporta la comparsa delle corrispondenti espressioni di potenza: , , eccetera. Infine, vengono considerati i gradi con indicatori irrazionali e le espressioni che li contengono:,.

La questione non è limitata alle espressioni di potenza elencate: la variabile penetra ulteriormente nell'esponente e, ad esempio, tali espressioni 2 x 2 +1 o ... E dopo l'incontro con, iniziano a comparire espressioni con potenze e logaritmi, ad esempio x 2 · lgx -5 · x lgx.

Quindi, abbiamo capito la domanda su cosa sono le espressioni esponenziali. Successivamente, impareremo a trasformarli.

Tipi di base di trasformazioni di espressioni di potenza

Con le espressioni esponenziali, puoi eseguire una qualsiasi delle trasformazioni identiche di base delle espressioni. Ad esempio, puoi espandere le parentesi, sostituire le espressioni numeriche con i loro valori, fornire termini simili, ecc. Naturalmente, in questo caso è necessario seguire la procedura accettata per l'esecuzione delle azioni. Ecco alcuni esempi.

Esempio.

Valutare il valore dell'espressione esponenziale 2 3 · (4 2 −12).

Soluzione.

In base all'ordine di esecuzione delle azioni, eseguiamo prima le azioni tra parentesi. Lì, in primo luogo, sostituiamo la potenza di 4 2 con il suo valore 16 (vedi se necessario), e in secondo luogo, calcoliamo la differenza 16−12 = 4. Abbiamo 2 3 (4 2 −12) = 2 3 (16−12) = 2 3 4.

Nell'espressione risultante, sostituisci la potenza 2 3 con il suo valore 8, quindi calcola il prodotto 8 4 = 32. Questo è il valore desiderato.

Così, 2 3 (4 2 −12) = 2 3 (16−12) = 2 3 4 = 8 4 = 32.

Risposta:

2 3 (4 2 −12) = 32.

Esempio.

Semplifica le espressioni di potenza 3 un 4 b −7 −1 + 2 un 4 b −7.

Soluzione.

Ovviamente, questa espressione contiene termini simili 3 · a 4 · b -7 e 2 · a 4 · b -7, e possiamo portarli:.

Risposta:

3 a 4 b −7 −1 + 2 a 4 b −7 = 5 a 4 b −7 −1.

Esempio.

Immagina un'espressione con poteri come un prodotto.

Soluzione.

Per far fronte al compito, la rappresentazione del numero 9 sotto forma di una potenza di 3 2 e il successivo uso della formula per la moltiplicazione abbreviata è la differenza dei quadrati:

Risposta:

Ci sono anche una serie di trasformazioni identiche inerenti alle espressioni di potere. Poi li analizzeremo.

Lavorare con base ed esponente

Esistono gradi, la cui base e/o esponente non sono solo numeri o variabili, ma alcune espressioni. Ad esempio, diamo i record (2 + 0,37) 5-3.7 e (a (a + 1) -a 2) 2 (x + 1).

Quando si lavora con tali espressioni, è possibile sostituire sia l'espressione basata sul grado che l'espressione nell'esponente con un'espressione identica uguale sull'ODZ delle sue variabili. In altre parole, possiamo, secondo le regole a noi note, trasformare separatamente la base del grado e separatamente - l'esponente. È chiaro che a seguito di questa trasformazione si otterrà un'espressione identicamente uguale a quella originaria.

Tali trasformazioni ci consentono di semplificare le espressioni con poteri o di raggiungere altri obiettivi di cui abbiamo bisogno. Ad esempio, nell'espressione esponenziale sopra (2 + 0,3 · 7) 5-3.7, puoi eseguire azioni con i numeri in base ed esponente, che ti permetteranno di andare alla potenza 4.1 1.3. E dopo aver ampliato le parentesi e ridotto termini simili nella base del grado (a (a + 1) −a 2) 2 (x + 1), otteniamo un'espressione di potenza di una forma più semplice a 2

Utilizzo delle proprietà di alimentazione

Uno dei principali strumenti per convertire le espressioni con poteri è l'uguaglianza, la riflessione. Ricordiamo i principali. Per qualsiasi numero positivo a e b e numeri reali arbitrari r e s, sono vere le seguenti proprietà di potenza:

a r a s = a r + s;
a r: a s = a r − s;
(a b) r = a r b r;
(a: b) r = a r: b r;
(a r) s = a r s.

Nota che per esponenti naturali, interi e anche positivi, le restrizioni sui numeri a e b potrebbero non essere così rigide. Ad esempio, per i numeri naturali m e n, l'uguaglianza a m a n = a m + n è vera non solo per a positivo, ma anche per negativo e per a = 0.

A scuola, l'attenzione principale quando si trasformano le espressioni di potere è focalizzata proprio sulla capacità di scegliere una proprietà adatta e applicarla correttamente. In questo caso, le basi dei gradi sono generalmente positive, il che consente di utilizzare le proprietà dei gradi senza restrizioni. Lo stesso vale per la trasformazione di espressioni contenenti variabili nelle basi dei gradi: l'intervallo di valori ammissibili delle variabili è solitamente tale che su di esso le basi assumono solo valori positivi, il che consente di utilizzare liberamente le proprietà dei gradi. In generale, è necessario chiedersi costantemente se in questo caso sia possibile applicare qualsiasi proprietà dei gradi, poiché l'uso impreciso delle proprietà può portare a un restringimento dell'ODV e ad altri problemi. Questi punti sono discussi in dettaglio e con esempi nell'articolo sulla conversione di espressioni utilizzando le proprietà dei gradi. Qui ci limitiamo a pochi semplici esempi.

Esempio.

Immaginiamo l'espressione a 2.5 · (a 2) -3: a -5.5 come una potenza di base a.

Soluzione.

Innanzitutto, trasformiamo il secondo fattore (a 2) -3 per la proprietà di elevare una potenza a potenza: (a 2) −3 = a 2 (−3) = a −6... L'espressione esponenziale originale assumerà allora la forma a 2.5 · a -6: a -5.5. Ovviamente, resta da usare le proprietà di moltiplicazione e divisione delle potenze con la stessa base, abbiamo
a 2,5 a -6: a -5,5 =
a 2,5−6: a -5,5 = a -3,5: a -5,5 =
a -3,5 - (- 5,5) = a 2.

Risposta:

a 2,5 (a 2) -3: a -5,5 = a 2.

Le proprietà di potenza vengono utilizzate sia da sinistra a destra che da destra a sinistra quando si trasformano le espressioni esponenziali.

Esempio.

Trova il valore dell'espressione esponenziale.

Soluzione.

L'uguaglianza (a b) r = a r b r, applicata da destra a sinistra, consente di passare dall'espressione originale al prodotto della forma e oltre. E quando si moltiplicano i gradi con le stesse basi, gli indicatori si sommano: .

È stato possibile eseguire la trasformazione dell'espressione originale in un altro modo:

Risposta:

Esempio.

Data l'espressione esponenziale a 1,5 −a 0,5 −6, inserisci la nuova variabile t = a 0,5.

Soluzione.

Il grado a 1,5 può essere rappresentato come 0,5 · 3 e ulteriormente, in base alla proprietà del grado al grado (ar) s = ar · s, applicato da destra a sinistra, trasformarlo nella forma (a 0,5) 3 . Così, a 1,5 −a 0,5 −6 = (a 0,5) 3 −a 0,5 −6... Ora è facile introdurre una nuova variabile t = a 0.5, otteniamo t 3 −t − 6.

Risposta:

t3 −t − 6.

Conversione di frazioni contenenti potenze

Le espressioni di potenza possono contenere frazioni con potenze o essere tali frazioni. Qualsiasi delle trasformazioni di base delle frazioni inerenti a frazioni di qualsiasi tipo è pienamente applicabile a tali frazioni. Cioè, le frazioni che contengono potenze possono essere cancellate, ridotte a un nuovo denominatore, lavorate separatamente con il loro numeratore e separatamente con il denominatore, ecc. Per illustrare le parole pronunciate, considera le soluzioni di diversi esempi.

Esempio.

Semplifica l'espressione esponenziale .

Soluzione.

Questa espressione esponenziale è una frazione. Lavoriamo con il suo numeratore e denominatore. Nel numeratore apriamo le parentesi e semplifichiamo l'espressione ottenuta successivamente utilizzando le proprietà delle potenze, e al denominatore diamo termini simili:

E cambiamo anche il segno del denominatore mettendo un meno davanti alla frazione: .

Risposta:

La riduzione delle frazioni contenenti potenze a un nuovo denominatore viene eseguita in modo simile alla riduzione delle frazioni razionali a un nuovo denominatore. In questo caso, viene trovato anche un fattore aggiuntivo e il numeratore e il denominatore della frazione vengono moltiplicati per esso. Quando si esegue questa azione, vale la pena ricordare che la riduzione a un nuovo denominatore può portare a un restringimento dell'ODV. Per evitare che ciò accada, è necessario che il fattore aggiuntivo non svanisca per nessun valore delle variabili dalle variabili ODZ per l'espressione originale.

Esempio.

Riduci le frazioni a un nuovo denominatore: a) al denominatore a, b) al denominatore.

Soluzione.

a) In questo caso, è abbastanza facile capire quale fattore aggiuntivo aiuta a ottenere il risultato desiderato. Questo è un fattore di a 0.3, poiché a 0.7 · a 0.3 = a 0.7 + 0.3 = a. Si noti che nell'intervallo dei valori consentiti della variabile a (questo è l'insieme di tutti i numeri reali positivi) il grado a 0,3 non svanisce, quindi abbiamo il diritto di moltiplicare numeratore e denominatore della frazione data per questo ulteriore fattore:

b) Guardando più da vicino il denominatore, puoi scoprire che

e moltiplicando questa espressione per darà la somma dei cubi e, cioè,. E questo è il nuovo denominatore a cui dobbiamo ridurre la frazione originale.

È così che abbiamo trovato un fattore aggiuntivo. Sull'intervallo di valori validi delle variabili x e y, l'espressione non svanisce, quindi possiamo moltiplicare il numeratore e il denominatore della frazione per esso:

Risposta:

un) , B) .

Anche l'abbreviazione delle frazioni contenenti potenze non è una novità: numeratore e denominatore sono rappresentati come un numero di fattori, e gli stessi fattori del numeratore e del denominatore vengono cancellati.

Esempio.

Riduci la frazione: a) , B).

Soluzione.

a) Innanzitutto, numeratore e denominatore possono essere ridotti dei numeri 30 e 45, che è 15. Inoltre, ovviamente, si può eseguire una riduzione di x 0,5 +1 e di ... Ecco cosa abbiamo:

b) In questo caso gli stessi fattori al numeratore e al denominatore non sono immediatamente visibili. Per ottenerli, dovrai eseguire trasformazioni preliminari. In questo caso, consistono nel scomporre il denominatore in fattori secondo la formula per la differenza dei quadrati:

Risposta:

un)

B) .

Ridurre le frazioni a un nuovo denominatore e ridurre le frazioni viene utilizzato principalmente per eseguire azioni con le frazioni. Le azioni vengono eseguite secondo regole note. Quando si aggiungono (sottraendo) le frazioni, vengono portate a un denominatore comune, dopo di che vengono aggiunti (sottratti) i numeratori e il denominatore rimane lo stesso. Il risultato è una frazione il cui numeratore è il prodotto dei numeratori e il denominatore è il prodotto dei denominatori. La divisione per frazione è la moltiplicazione per l'inverso della frazione.

Esempio.

Segui i passi .

Soluzione.

Innanzitutto, sottraiamo le frazioni tra parentesi. Per fare questo, li portiamo a un denominatore comune, che è , dopo di che sottraiamo i numeratori:

Ora moltiplichiamo le frazioni:

Ovviamente è possibile annullare per una potenza di x 1/2, dopo di che si ha .

Puoi anche semplificare l'espressione esponenziale nel denominatore usando la formula della differenza di quadrati: .

Risposta:

Esempio.

Semplifica l'espressione esponenziale .

Soluzione.

Ovviamente, questa frazione può essere annullata di (x 2,7 +1) 2, questo dà la frazione ... È chiaro che occorre fare qualcos'altro con i gradi di x. Per fare ciò, trasformiamo la frazione risultante in un prodotto. Questo ci dà l'opportunità di usare la proprietà di dividere i gradi con le stesse basi: ... E alla fine del processo, si passa dall'ultimo prodotto a una frazione.

Risposta:

E aggiungiamo anche che è possibile e in molti casi desiderabile trasferire moltiplicatori con esponente negativo dal numeratore al denominatore o dal denominatore al numeratore, cambiando il segno dell'esponente. Tali trasformazioni spesso semplificano ulteriori azioni. Ad esempio, un'espressione esponenziale può essere sostituita con.

Conversione di espressioni con radici e potenze

Spesso nelle espressioni in cui sono richieste alcune trasformazioni, insieme alle potenze con esponenti frazionari, sono presenti anche le radici. Per trasformare una tale espressione nella forma desiderata, nella maggior parte dei casi è sufficiente andare solo alle radici o solo alle potenze. Ma poiché è più conveniente lavorare con i gradi, di solito vanno dalle radici ai gradi. Tuttavia, è consigliabile eseguire tale transizione quando l'ODZ delle variabili per l'espressione originale consente di sostituire le radici con le potenze senza la necessità di fare riferimento al modulo o di dividere l'ODV in più intervalli (ne abbiamo discusso in dettaglio in l'articolo il passaggio dalle radici ai poteri e viceversa introduce una laurea con un indicatore irrazionale, che consente di parlare di una laurea con un indicatore reale arbitrario. funzione esponenziale, che è analiticamente fissato dal grado, alla base del quale è il numero, e nell'indicatore - la variabile. Quindi ci troviamo di fronte a espressioni esponenziali contenenti numeri nella base del grado e nell'esponente - espressioni con variabili, e naturalmente è necessario eseguire trasformazioni di tali espressioni.

Va detto che la trasformazione di espressioni di questo tipo di solito deve essere eseguita durante la risoluzione equazioni esponenziali e disuguaglianze esponenziali e queste conversioni sono piuttosto semplici. Nella stragrande maggioranza dei casi, si basano sulle proprietà del grado e sono principalmente finalizzate all'introduzione di una nuova variabile in futuro. Possiamo dimostrarli con l'equazione 5 2 x + 1 −3 5 x 7 x −14 7 2 x − 1 = 0.

Innanzitutto, i gradi, in cui si trova la somma di una variabile (o espressioni con variabili) e un numero, vengono sostituiti da prodotti. Questo vale per il primo e l'ultimo termine dell'espressione a sinistra:
5 2 x 5 1 −3 5 x 7 x −14 7 2 x 7 −1 = 0,
5 5 2 x −3 5 x 7 x −2 7 2 x = 0.

Inoltre, entrambi i lati dell'uguaglianza sono divisi dall'espressione 7 2 x, che assume solo valori positivi sull'ODZ della variabile x per l'equazione originale (questa è una tecnica standard per risolvere equazioni di questo tipo, non lo siamo parlandone ora, quindi concentrati sulle successive trasformazioni di espressioni con poteri ):

Le frazioni con poteri sono ora cancellate, il che dà .

Infine, il rapporto dei gradi con gli stessi esponenti è sostituito dai gradi delle relazioni, che porta all'equazione che è equivalente a ... Le trasformazioni eseguite consentono di introdurre una nuova variabile, che riduce la soluzione dell'equazione esponenziale originaria alla soluzione dell'equazione quadratica

I. V. Boykov, L. D. Romanova Raccolta di compiti per la preparazione all'esame. Parte 1. Penza 2003.

Insegnante di matematica: Nashkenova A.N. Maybalik scuola secondaria Schema della lezione sull'argomento "Laurea con un indicatore razionale"

(algebra, grado 11)

Obiettivi della lezione:

Ampliare e approfondire la conoscenza degli studenti del grado di numero; familiarizzare gli studenti con il concetto di laurea con un indicatore razionale e le loro proprietà;

Sviluppare conoscenze, abilità e abilità per calcolare i valori delle espressioni utilizzando le proprietà;

Continuare a lavorare sullo sviluppo delle competenze per analizzare, confrontare, evidenziare la cosa principale, definire e spiegare concetti;

Formare competenze comunicative, capacità di argomentare le proprie azioni, favorire l'indipendenza, la diligenza.

Attrezzatura: libro di testo, schede di dispense, laptop,materiale di presentazione Presa della corrente ;

Tipo di lezione: una lezione di studio e consolidamento primario di nuove conoscenze.

Piano della lezione:

1.Org. momento. - 1 minuto.

2. Motivazione della lezione.2 minuti

3. Attualizzazione delle conoscenze di base. - 5 minuti.

4. Apprendimento di nuovo materiale. - 15 minuti.

5. Minuto di esercizio - 1 min.

6. Consolidamento primario del materiale studiato - 10 min

7. Lavoro indipendente. - 7 minuti

8. Compiti a casa. - 2 minuti.

9.Riflessione - 1 min.

10. Riepilogo della lezione. - 1 minuto.

Durante le lezioni

1. Momento organizzativo

Atteggiamento emotivo alla lezione.

Vorrei lavorare, vorrei

opera,
Ti auguro successo oggi.
Dopotutto, in futuro, tutto questo è per te

tornare utile.
E sarà più facile per te in futuro

studio(Diapositiva numero 1)

2. Motivazione della lezione

L'elevamento a potenza e l'estrazione della radice, come le quattro operazioni aritmetiche, sono emerse come risultato di un'esigenza pratica. Quindi, insieme al compito di calcolare l'area di un quadrato, il latoun come è noto, si è verificato il problema inverso: “Quanto deve avere il lato di un quadrato affinché la sua area sia uguale av. Nei secoli 14-15 apparvero in Europa occidentale le banche, che davano soldi per la crescita a principi e mercanti, finanziavano lunghi viaggi e campagne di conquista per alto interesse. Per facilitare il calcolo dell'interesse composto, abbiamo compilato delle tabelle, secondo le quali è stato immediatamente possibile scoprire quanto doveva essere pagato tramiteNS anni se l'importo è stato preso in prestitoun SuR % annuale. L'importo pagato è espresso dalla formula: S = a (1 + ) NS A volte il denaro è stato preso in prestito non per un numero intero di anni, ma ad esempio per 2 anni 6 mesi. Se dopo 2,5 anni l'importoun applica a aq , poi nei prossimi 2,5 anni aumenterà di un altroQ volte e diventa ugualeaq 2 ... Dopo 5 anni:a = (1 + 5 , perciò Q 2 = (1 + 5 e si intende Q =

(Diapositiva 2) .

È così che è nata l'idea di un esponente frazionario.

3. Attualizzazione delle conoscenze di base.

Domande:

1. Cosa significa il record;un NS

2. Che cos'è un ?

3. Che cos'è NS ?

4. un -NS =?

5. Annota le proprietà del grado con un intero esponente su un quaderno.

6. Quali numeri sono naturali, interi, razionali? Disegnali usando i cerchi di Eulero.(Diapositiva 3)

Risposte: 1. Grado con esponente intero

2. un- base

3. NS- esponente

4. un -NS =

5. Proprietà dell'esponente intero:

un m * un n = a (m + n) ;

un m : un n = a (m-n) ( a un non pari zero );

(un m ) n = a (m * n) ;

(a * b) n = a n * B n ;

(a/b) n = (a n ) / (B n ) (a B non uguale a zero);

un 1 = un;

un 0 = 1 (per un non uguale a zero);

Queste proprietà saranno valide per qualsiasi numero a, b e qualsiasi intero m e n.

6.1,2,3, ... - numeri positivi - un insieme di numeri naturali -n

0, -1, -2, -3, .. numero O e numeri negativi - un insieme di numeri interi -Z

Q , - numeri frazionari (negativi e positivi) - insieme di numeri razionali -Q Z

cerchi di Eulero (diapositiva 4)

4. Apprendimento di nuovo materiale.

Lascia stare. un - numero non negativo e devi elevarlo a una potenza frazionaria ... Conosci l'uguaglianza (un m ) n = a m n (diapositiva 4) , cioè. la regola per elevare l'esponente all'esponente. Nell'uguaglianza di cui sopra, supponiamo che m =, quindi otteniamo: (un ) NS = a = a (diapositiva 4)

Da ciò possiamo concludere che èun radice NS -esimo grado del numeroun , cioè. un = . ne consegue che (un NS ) = NS = a (diapositiva 4).

Quindi un = (a ) m = (a m ) = m . ( diapositiva 4 ).

Vale quindi la seguente uguaglianza:un = m (diapositiva 4)

Definizione: il grado di un numero non negativo un con un indicatore razionale , dove - una frazione irriducibile, chiamata valore della radice n-esima del numero un T .

Pertanto, per definizione un = m (diapositiva 5)

Diamo un'occhiata all'esempio 1 : Scrivi il grado con l'esponente razionale nella forma della radice n-esima:

1)5 2)3,7 -0,7 3) ( ) (diapositiva 6) Soluzione: 1) 5 = 2 = 2) 3,7 -0,7 = -7 3) ( ) = ( diapositiva 7) Sulle potenze con esponente razionale si possono compiere le azioni di moltiplicazione, divisione, elevazione a potenza ed estrazione di radice secondo le stesse regole delle potenze con esponente intero e delle potenze con le stesse basi:un = a + un = un - (un ) = a * (a * b) = a * v ) = un / v dove n, Q - naturale, t, p - interi. (diapositiva 8) 5. Minuto di esercizio

Ho guardato a destra

Hanno girato lo sguardo a sinistra

Abbiamo guardato intorno al soffitto

Tutti abbiamo guardato avanti.

Uno - piega - piega,

Due ─ piegare - allungare,

Tre - tre applausi nelle tue mani,

Testa tre annuisce.

Cinque e sei siedono in silenzio.

E di nuovo in viaggio! (diapositiva 9)

6. Consolidamento primario del materiale studiato:

Pagina 51, n. 90, n. 91: fai da te su un quaderno,

con assegno alla lavagna

7 lavoro indipendente

opzione 1

(Diapositiva 10)

opzione 1

(Diapositiva 11)

Eseguire un lavoro indipendente con verifica reciproca.

Risposte:

opzione 1

(Diapositiva 12)

Quindi, oggi nella lezione abbiamo familiarizzato con il concetto di laurea con un indicatore razionale e abbiamo imparato a scrivere sotto forma di radici, applicare le proprietà di base dei gradi quando si trovano i valori delle espressioni numeriche.8. Compiti a casa: # 92, # 93 Informazioni sui compiti

9. Riflessione

(Diapositiva 13)

10. Riepilogo della lezione:

Quali sono le somiglianze e le differenze tra il grado con l'indicatore intero e il grado con l'indicatore frazionario? (somiglianza: tutte le proprietà di un grado con esponente intero esistono anche per un grado con esponente razionale;

differenza: gradi)

Elenca le proprietà di un grado con esponente razionale

La lezione è finita oggi
Non puoi essere trovato più amichevole.
Ma tutti dovrebbero sapere:
Conoscenza, perseveranza, lavoro
Condurranno al progresso nella vita.
Grazie per la lezione! (diapositiva 14)

La lezione video "Laurea con un indicatore razionale" contiene materiale educativo visivo per condurre una lezione su questo argomento. La lezione video contiene informazioni sul concetto di laurea con un indicatore razionale, proprietà, tali gradi, nonché esempi che descrivono l'uso di materiale didattico per risolvere problemi pratici. Il compito di questa lezione video è presentare visivamente e chiaramente materiale didattico, facilitarne la padronanza e la memorizzazione da parte degli studenti, formare la capacità di risolvere problemi utilizzando i concetti appresi.

I principali vantaggi della lezione video sono la capacità di eseguire visivamente trasformazioni e calcoli, la capacità di utilizzare effetti di animazione per migliorare l'efficienza dell'apprendimento. La guida vocale aiuta a sviluppare un discorso matematico corretto e consente anche di sostituire la spiegazione dell'insegnante, liberandolo per il lavoro individuale.

Il video tutorial inizia introducendo l'argomento. Collegando lo studio di un nuovo argomento con materiale studiato in precedenza, si propone di ricordare che n è altrimenti indicato con a 1 / n per n naturale e positivo a. Questa rappresentazione dell'ennesima radice viene visualizzata sullo schermo. Successivamente, si propone di considerare cosa significa l'espressione a m / n, in cui a è un numero positivo e m / n è una frazione. Si dà la definizione di grado con esponente razionale a m / n = n √a m. Allo stesso tempo, è stato notato che n può essere un numero naturale e m un numero intero.

Dopo aver determinato il grado con un esponente razionale, il suo significato è rivelato da esempi: (5/100) 3/7 = 7 √ (5/100) 3. Mostra anche un esempio in cui una potenza decimale viene convertita in una frazione da rappresentare come radice: (1/7) 1,7 = (1/7) 17/10 = 10 √ (1/7) 17 e un esempio con un esponente negativo: 3 -1/8 = 8 √3 -1.

La particolarità del caso particolare in cui la base del grado è zero è indicata separatamente. Si noti che questo grado ha senso solo con un esponente frazionario positivo. In questo caso, il suo valore è zero: 0 m / n = 0.

Si nota un'altra caratteristica del grado con un esponente razionale: un grado con un esponente frazionario non può essere considerato con un esponente frazionario. Si riportano esempi di errata scrittura del titolo di studio: (-9) -3/7, (-3) -1/3, 0 -1/5.

Più avanti nella lezione video, vengono considerate le proprietà di una laurea con un indicatore razionale. Si noti che le proprietà di un grado con esponente intero saranno valide anche per un grado con esponente razionale. Si propone di richiamare l'elenco delle proprietà valide anche in questo caso:

Quando si moltiplicano i gradi con le stesse basi, i loro esponenti si sommano: a p a q = a p + q.
La divisione dei gradi con le stesse basi si riduce ad un grado con una data base e la differenza tra gli esponenti dei gradi: a p: a q = a p-q.
Se aumentiamo il grado di un certo grado, alla fine otteniamo il grado con la base data e il prodotto degli indicatori: (a p) q = a pq.

Tutte queste proprietà sono valide per gradi con esponenti razionali p, q e base positiva a> 0. Le trasformazioni di grado sono valide anche quando si espandono le parentesi:

(ab) p = a p b p - elevare a una certa potenza con un esponente razionale del prodotto di due numeri si riduce al prodotto di numeri, ciascuno dei quali è elevato a una data potenza.
(a / b) p = a p / b p - elevare a una potenza con un esponente razionale della frazione viene ridotto a una frazione, il cui numeratore e denominatore sono elevati a questa potenza.

La lezione video discute la soluzione di esempi che utilizzano le proprietà considerate dei gradi con un esponente razionale. Nel primo esempio si propone di trovare il valore di un'espressione che contiene le variabili x in una potenza frazionaria: (x 1/6 -8) 2 -16x 1/6 (x -1/6 -1). Nonostante la complessità dell'espressione, può essere risolta semplicemente usando le proprietà dei gradi. La soluzione del problema inizia con una semplificazione dell'espressione, che utilizza la regola per elevare a potenza una potenza con esponente razionale, nonché moltiplicare potenze con la stessa base. Dopo aver sostituito il valore dato x = 8 nell'espressione semplificata x 1/3 +48, è facile ottenere il valore - 50.

Nel secondo esempio è necessario cancellare la frazione il cui numeratore e denominatore contengono potenze con esponente razionale. Usando le proprietà del grado, selezioniamo dalla differenza il fattore x 1/3, che viene poi cancellato al numeratore e al denominatore, e usando la formula per la differenza dei quadrati, il numeratore viene scomposto in fattori, il che dà ulteriori riduzioni degli stessi fattori al numeratore e al denominatore. Il risultato di tali trasformazioni è una breve frazione x 1/4 +3.

La lezione video "Laurea con un indicatore razionale" può essere utilizzata al posto dell'insegnante che spiega il nuovo argomento della lezione. Inoltre, questo manuale contiene informazioni sufficientemente complete per lo studio autonomo da parte di uno studente. Il materiale può essere utile anche per la didattica a distanza.

Lezione numero 30 (Algebra e inizio analisi, voto 11)

Argomento della lezione: Grado razionale.

Obiettivo della lezione: 1 ... Espandi il concetto di laurea, dai il concetto di laurea con un indicatore razionale; insegnare come tradurre una laurea con un esponente razionale nella radice e viceversa; calcolare le potenze con un esponente razionale.

2. Sviluppo della memoria, pensiero.

3. Formazione di attività.

"Lascia che qualcuno provi a cancellare

da una laurea in matematica e vedrà

Che non puoi andare lontano senza di loro" MV Lomonosov

Durante le lezioni.

I. Comunicazione dell'argomento e scopo della lezione.

II. Ripetizione e consolidamento del materiale passato.

1. Analisi di esempi domestici irrisolti.

2. Controllo del lavoro indipendente:

Opzione 1.

1. Risolvi l'equazione: √ (2x - 1) = 3x - 12

2. Risolvi la disuguaglianza: √ (3x - 2) ≥ 4 - x

Opzione 2.

1. Risolvi l'equazione: 3 - 2x = (7x + 32)

2. Risolvi la disuguaglianza: √ (3x + 1) ≥ x - 1

III. Imparare nuovo materiale.

1 ... Ricordiamo l'estensione della nozione di numeri: N є Z є Q є R.

Questo è meglio rappresentato nella forma del diagramma seguente:

Naturale (N)

Zero

Numeri non negativi

Numeri negativi

Numeri frazionari

Interi (Z)

Irrazionale

Razionale (Q)

Numeri reali

2. Nelle classi inferiori è stato definito il concetto di grado di un numero con esponente intero. a) Ricordare la definizione del grado a) con naturale, b) con intero negativo, c) con esponente zero.Sottolinea che l'espressione a n ha senso per tutti gli interi n e qualsiasi valore di a, eccetto per a = 0 e n≤0.

b) Elenca le proprietà dei gradi con esponente intero.

3. Lavoro orale.

1). Calcola: 1 -5; 4 -3; (-100 ; (-5) -2; (1/2) -4; (3/7) -1.

2). Scrivilo come esponente negativo:

1/4 5; 1/21 3; 1/x7; 1/a 9.

3) .Confronta con l'unità: 12-3 ; 21 0 ; (0,6) -5 ; (5/19) -4 .

4 ... Ora devi capire il significato delle espressioni 3 0,4 ; 4 5/7 ; 5 -1/2 eccetera. Per questo, è necessario generalizzare il concetto di grado in modo tale che tutte le proprietà elencate dei gradi siano soddisfatte. Consideriamo l'uguaglianza (a m / n) n = un m ... Allora, per la definizione di radice n-esima, è ragionevole assumere che a m / n sarà l'ennesima radice del numero a m ... Viene data la definizione del grado con un indicatore razionale.

5. Considera gli esempi 1 e 2 dal libro di testo.

6. Facciamo alcune osservazioni relative al concetto di grado con esponente razionale.

Osservazione 1 : Per ogni a> 0 e un numero razionale r, il numero a r> 0

Osservazione 2 : Per la proprietà fondamentale delle frazioni, il numero razionale m / n può essere scritto come mk / nk per qualsiasi numero naturale k. Quindiil valore del grado non dipende dalla forma di scrittura del numero razionale, poiché a mk / nk = = nk √a mk = n √a m = a m / n

Nota 3: Per un Spieghiamolo con un esempio. Considera (-64) 1/3 = 3 -64 = -4. Invece: 1/3 = 2/6 e poi (-64) 1/ 3 = (-64) 2/6 = 6 √(-64) 2 = 6√64 2 = 6 √4 6 = 4. Otteniamo una contraddizione.

Un'espressione della forma a (m / n), dove n è un numero naturale, m è un numero intero e la base del grado a è maggiore di zero, si chiama grado con esponente frazionario. Inoltre vale la seguente uguaglianza. n√ (a m) = a (m / n).

Come già sappiamo, i numeri della forma m / n, dove n è un numero naturale e m è un intero, sono chiamati numeri frazionari o razionali. Da quanto sopra si ricava che il grado è definito per ogni esponente razionale e per ogni base positiva del grado.

Per qualsiasi numero razionale p, q e qualsiasi a> 0 e b> 0, valgono le seguenti uguaglianze:

1. (a p) * (a q) = a (p + q)
2. (a p) :( b q) = a (p-q)
3. (a p) q = a (p * q)
4. (a * b) p = (a p) * (b p)
5. (a / b) p = (a p) / (b p)

Queste proprietà sono ampiamente utilizzate quando si convertono varie espressioni contenenti potenze con esponenti frazionari.

Esempi di trasformazioni di espressioni contenenti una potenza con esponente frazionario

Diamo un'occhiata ad alcuni esempi che dimostrano come utilizzare queste proprietà per trasformare le espressioni.

1. Calcola 7 (1/4) * 7 (3/4).

7 (1/4) * 7 (3/4) = z (1/4 + 3/4) = 7.

2. Calcola 9 (2/3): 9 (1/6).

9 (2/3) : 9 (1/6) = 9 (2/3 - 1/6) = 9 (1/2) = √9 = 3.

3. Calcola (16 (1/3)) (9/4).

(16 (1/3)) (9/4) = 16 ((1/3)*(9/4)) =16 (3/4) = (2 4) (3/4) = 2 (4*3/4) = 2 3 = 8.

4. Calcola 24 (2/3).

24 (2/3) = ((2 3)*3) (2/3) = (2 (2*2/3))*3 (2/3) = 4*3√(3 2)=4*3√9.

5. Calcola (8/27) (1/3).

(8/27) (1/3) = (8 (1/3))/(27 (1/3)) = ((2 3) (1/3))/((3 3) (1/3))= 2/3.

6. Semplifica l'espressione ((a (4/3)) * b + a * b (4/3)) / (3√a + 3√b)

((a (4/3)) * b + a * b (4/3)) / (3√a + 3√b) = (a * b * (a (1/3) + b (1/3 ))) / (1/3) + b (1/3)) = a * b.

7. Calcola (25 (1/5)) * (125 (1/5)).

(25 (1/5))*(125 (1/5)) =(25*125) (1/5) = (5 5) (1/5) = 5.

8. Semplifica l'espressione

(a (1/3) - a (7/3)) / (a (1/3) - a (4/3)) - (a (-1/3) - a (5/3)) / ( un (2/3) + un (-1/3)).
(a (1/3) - a (7/3)) / (a (1/3) - a (4/3)) - (a (-1/3) - a (5/3)) / ( un (2/3) + un (-1/3)) =
= ((a (1/3)) * (1-a 2)) / ((a (1/3)) * (1-a)) - ((a (-1/3)) * (1- a 2)) / ((a (-1/3)) * (1 + a)) =
= 1 + a - (1-a) = 2 * a.

Come puoi vedere, usando queste proprietà, puoi semplificare notevolmente alcune espressioni che contengono potenze con esponenti frazionari.